Postscript version of this file

STAT 380 Lecture 1

Course outline

Reading for Today's Lecture: Chapters 1, 2 and 3 of Ross.

Goals of Today's Lecture:

• Give an overview of the course.

• Do some review by example.

Course Outline

• Review of Basic Probability

  • Distributions

  • Expectation and moments

  • Moment generating functions

  • Independence, conditioning

• Markov Chains

• Poisson Processes

• Birth and Death Processes

• Brownian Motion

• Monte Carlo Simulation techniques
  • Random number generators

  • Generating random variables

Today's lecture Summary

• Three examples to review
  • basic probability: sample space, events, random variables, expected value

  • standard distributions: Binomial, Geometric, Poisson

  • conditional probability, independence

  • Baye's rule

• Introduction to modelling

Basic Examples

Example 1: Three cards: one red on both sides, one black on both sides, one black on one side, red on the other. Shuffle, pick card at random. Side up is Black. What is the probability the side down is Black?

Solution: To do this carefully, enumerate sample space, $\Omega$, of all possible outcomes. Six sides to the three cards. Label three red sides 1, 2, 3 with sides 1, 2 on the all red card (card # 1). Label three black sides 4, 5, 6 with 3, 4 on opposite sides of mixed card (card #2). Define some events:
$$\begin{align*}A_i & = \{\text{side $i$\space shows face up}\} \\ B & = \{\text{... ...showing is black}\} \\ C_j & = \{\text{card $j$\space is chosen}\} \end{align*}$$

One representation $\Omega=\{1,2,3,4,5,6\}$. Then $A_i = \{i\}$, $B=\{4,5,6\}$, $C_1=\{1,2\}$ and so on.

Modelling: assumptions about some probabilities; deduce probabilities of other events. In example simplest model is

All of the A_i are equally likely.

Apply two rules:

$$P(\cup_1^6 A_i) = \sum_1^6 P(A_i) \quad\text{and} \quad P(\Omega) = 1$$

to get, for $i=1,\ldots,6$,

$$P(A_i) = \frac{1}{6}$$

Question was about down side of card. We have been told B has happened. Event that a black side is down is $D=\{3,5,6\}$. (Of course B has happened rules out 3.)

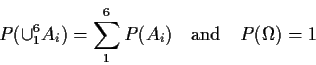
Definition of conditional probability:

$$P(D\vert B) = \frac{P(D\cap B)}{P(B)} = \frac{P(\{5,6\})}{P(\{4,5,6\})} = \frac{2}{3}$$

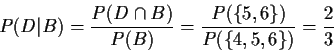
Example 2: Monte Hall, Let's Make a Deal. Monte shows you 3 doors. Prize hidden behind one. You pick a door. Monte opens a door you didn't pick; shows you no prize; offers to let you switch to the third door. Do you switch?