Postscript version of this page

STAT 380 Lecture 2

Today's lecture Summary

The Monte Hall problem to review

• basic probability: sample space, events, random variables, expected value

• conditional probability, independence

• Baye's rule

Example 2: Monte Hall, Let's Make a Deal. Monte shows you 3 doors. Prize hidden behind one. You pick a door. Monte opens a door you didn't pick; shows you no prize; offers to let you switch to the third door. Do you switch?

Sample space: typical element is (a,b,c) where a is number of door with prize, b is number of your first pick and c is door Monte opens with no prize.

(1,1,2)	(1,1,3)	(1,2,3)	(1,3,2)
(2,1,3)	(2,2,1)	(2,2,3)	(2,3,1)
(3,1,2)	(3,2,1)	(3,3,1)	(3,3,2)

Model? Traditionally we define events like

$$\begin{eqnarray*}A_i & = & \{\text{Prize behind door $i$ }\} \\ B_j & = & \{\text{You choose door $j$ }\} \end{eqnarray*}$$

and assume that each A_i has chance 1/3. We are assuming we have no prior reason to suppose Monte favours one door. But these and all other probabilities depend on the behaviour of people so are open to discussion.

The event LS, that you lose if you switch is

$$(A_1\cap B_1) \cup (A_2\cap B_2) \cup (A_3\cap B_3)$$

The natural modelling assumption, which captures the idea that you have no idea where the prize is hidden, is that each A_iis independent of each B_j, that is,

$$P(A_i \cap B_j) = P(A_i)P(B_j)$$

Usually we would phrase this assumption in terms of two random variables, M, the door with the prize, and C the door you choose. We are assuming that M and C are independent. Then
$$\begin{align*}P(LS) = & P(A_1\cap B_1) + P(A_2\cap B_2) \\ & \qquad + P(A_3\ca... ...rac{1}{3}\left\{P(B_1) + P(B_2) +P(B_3)\right\} \\ = &\frac{1}{3} \end{align*}$$

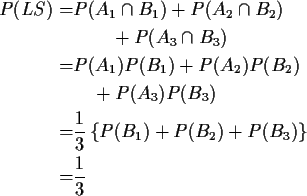
So the event you win by switching has probability 2/3 and you should switch.

Usual phrasing of problem. You pick 1, Monte shows 3. Should you take 2? Let S be rv S = door Monte shows you. Question:

P(M=1|C=1, S=3)

Modelling assumptions do not determine this; it depends on Monte's method for choosing door to show when he has a choice. Two simple cases:

1.

Monte picks at random so

P(S=3|M=1,C=1) = 1/2

2.

Monte chooses the door with the largest possible number:

P(S=3|M=1,C=1) = 1

Use Baye's rule:
$$\begin{multline*}P(M=1\vert C=1, S=3) \\ = \frac{P(M=1,C=1, S=3)}{P(C=1,S=3)} \end{multline*}$$
Numerator is
$$\begin{multline*}P(S=3\vert M=1,C=1) P(M=1,C=1) \\ = P(S=3\vert M=1,C=1)P(C=1)/3 \end{multline*}$$
Denominator is
$$\begin{multline*}P(S=3\vert M=1,C=1) P(M=1,C=1) \\ + P(S=3\vert M=2,C=1) P(M=2,C=1) \\ +P(S=3\vert M=3,C=1) P(M=3,C=1) \end{multline*}$$
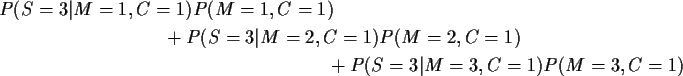
which simplifies to
$$\begin{multline*}P(S=3\vert M=1,C=1)P(M=1)P(C=1) \\ +1 \cdot P(M=2)P(C=1) \\ +0 \cdot P(M=3)P(C=1) \end{multline*}$$
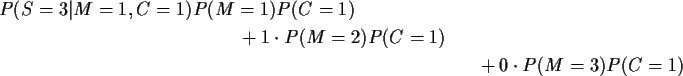
which in turn is

$$\left\{P(S=3\vert M=1,C=1)+1\right\}P(C=1)/3$$

For case 1 we get

$$P(M=1\vert C=1, S=3) = \frac{1/2}{1/2 + 1} = \frac{1}{3}$$

while for case 2 we get

$$P(M=1\vert C=1, S=3) = \frac{1}{1+1} =\frac{1}{2}$$

Notice that in case 2 if we pick door 1 and Monte shows us door 2 we should definitely switch. Notice also that it would be normal to assume that Monte used the case 1 algorithm to pick the door to show when he has a choice; otherwise he is giving the contestant information. If the contestant knows Monte is using algorithm 2 then by switching if door 2 is shown and not if door 3 is shown he wins 2/3 of the time which is as good as the always switch strategy.

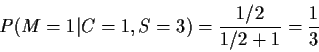
Example 3: Survival of family names. Traditionally: family name follows sons. Given man at end of 20th century. Probability descendant (male) with same last name alive at end of 21st century? or end of 30th century?

Simplified model: count generations not years. Compute probability, of survival of name for n generations.