Reading for Today's Lecture: Chapter 4 sections 1-3.
Goals of Today's Lecture:
Finding stationary initial distributions. Consider the ![]() for the weather example. The equation
for the weather example. The equation
Some more examples:
![\begin{displaymath}{\bf P}= \left[\begin{array}{cccc}
0 & 1/3 & 0 & 2/3
\\
1/3...
...\\
0 & 2/3 & 0 & 1/3
\\
2/3 & 0 & 1/3 & 0
\end{array}\right]
\end{displaymath}](img10.gif)
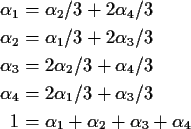
p:=matrix([[0,1/3,0,2/3],[1/3,0,2/3,0],
[0,2/3,0,1/3],[2/3,0,1/3,0]]);
[ 0 1/3 0 2/3]
[ ]
[1/3 0 2/3 0 ]
p := [ ]
[ 0 2/3 0 1/3]
[ ]
[2/3 0 1/3 0 ]
> p2:=evalm(p*p);
[5/9 0 4/9 0 ]
[ ]
[ 0 5/9 0 4/9]
p2:= [ ]
[4/9 0 5/9 0 ]
[ ]
[ 0 4/9 0 5/9]
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> p16:=evalm(p8*p8):
> p17:=evalm(p8*p8*p):
> evalf(evalm(p16));
[.5000000116 , 0 , .4999999884 , 0]
[ ]
[0 , .5000000116 , 0 , .4999999884]
[ ]
[.4999999884 , 0 , .5000000116 , 0]
[ ]
[0 , .4999999884 , 0 , .5000000116]
> evalf(evalm(p17));
[0 , .4999999961 , 0 , .5000000039]
[ ]
[.4999999961 , 0 , .5000000039 , 0]
[ ]
[0 , .5000000039 , 0 , .4999999961]
[ ]
[.5000000039 , 0 , .4999999961 , 0]
> evalf(evalm((p16+p17)/2));
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
[ ]
[.2500, .2500, .2500, .2500]
Next example:
![\begin{displaymath}p = \left[\begin{array}{cccc}
\frac{2}{5} & \frac{3}{5}
& 0 &...
...{3}{5}
\\
0 &0 &
\frac{1}{5} & \frac{4}{5}\end{array}\right]
\end{displaymath}](img17.gif)

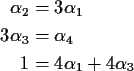
Pick ![]() in [0,1/4];
put
in [0,1/4];
put
![]() .
.
> p:=matrix([[2/5,3/5,0,0],[1/5,4/5,0,0],
[0,0,2/5,3/5],[0,0,1/5,4/5]]);
[2/5 3/5 0 0 ]
[ ]
[1/5 4/5 0 0 ]
p := [ ]
[ 0 0 2/5 3/5]
[ ]
[ 0 0 1/5 4/5]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[.2500000000 , .7500000000 , 0 , 0]
[ ]
[0 , 0 , .2500000000 , .7500000000]
[ ]
[0 , 0 , .2500000000 , .7500000000]
Notice that rows converge but to two different vectors:
Last example:
> p:=matrix([[2/5,3/5,0],[1/5,4/5,0],
[1/2,0,1/2]]);
[2/5 3/5 0 ]
[ ]
p := [1/5 4/5 0 ]
[ ]
[1/2 0 1/2]
> p2:=evalm(p*p):
> p4:=evalm(p2*p2):
> p8:=evalm(p4*p4):
> evalf(evalm(p8*p8));
[.2500000000 .7500000000 0 ]
[ ]
[.2500000000 .7500000000 0 ]
[ ]
[.2500152588 .7499694824 .00001525878906]
Basic distinguishing features: pattern of 0s in matrix ![]() .
.