Reading : Chapters 1, 2 and 3 of Ross.
Goals for the Week:
Course outline:
Example 1: Three cards: one red on both sides, one black on both sides, one black on one side, red on the other. Shuffle, pick card at random. Side up is Black. What is the probability the side down is Black?
Solution: To do this carefully, enumerate sample space,
![]() , of all possible outcomes. Six sides to the three cards.
Label three red sides 1, 2, 3 with sides 1, 2 on the all red card (card
# 1).
Label three black sides 4, 5, 6 with 3, 4 on opposite sides of mixed
card (card #2). Define some events:
, of all possible outcomes. Six sides to the three cards.
Label three red sides 1, 2, 3 with sides 1, 2 on the all red card (card
# 1).
Label three black sides 4, 5, 6 with 3, 4 on opposite sides of mixed
card (card #2). Define some events:
One representation
![]() . Then
. Then
![]() ,
,
![]() ,
,
![]() and so on.
and so on.
Modelling: assumptions about some probabilities; deduce probabilities of other events. In example simplest model is
Apply two rules:
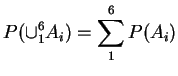 and
and
Definition of conditional probability:

Example 2: Monte Hall, Let's Make a Deal. Monte shows you 3 doors. Prize hidden behind one. You pick a door. Monte opens a door you didn't pick; shows you no prize; offers to let you switch to the third door. Do you switch?
Sample space: typical element is ![]() where
where ![]() is number
of door with prize,
is number
of door with prize, ![]() is number of your first pick and
is number of your first pick and ![]() is
door Monte opens with no prize.
is
door Monte opens with no prize.
| (1,1,2) | (1,1,3) | (1,2,3) | (1,3,2) |
| (2,1,3) | (2,2,1) | (2,2,3) | (2,3,1) |
| (3,1,2) | (3,2,1) | (3,3,1) | (3,3,2) |
Model? Traditionally we define events like
The event ![]() , that you lose if you switch is
, that you lose if you switch is
 |
||
So the event you win by switching has probability 2/3 and you should switch.
Usual phrasing of problem. You pick 1, Monte shows 3. Should
you take 2? Let ![]() be rv
be rv ![]() door Monte
shows you. Question:
door Monte
shows you. Question:
Modelling assumptions do not determine this; it depends on Monte's method for choosing door to show when he has a choice. Two simple cases:
Use Bayes' rule:




For case 1 we get


Notice that in case 2 if we pick door 1 and Monte shows us door 2 we should definitely switch. Notice also that it would be normal to assume that Monte used the case 1 algorithm to pick the door to show when he has a choice; otherwise he is giving the contestant information. If the contestant knows Monte is using algorithm 2 then by switching if door 2 is shown and not if door 3 is shown he wins 2/3 of the time which is as good as the always switch strategy.
Example 3: Survival of family names. Traditionally: family name follows sons. Given man at end of 20th century. Probability descendant (male) with same last name alive at end of 21st century? or end of 30th century?
Simplified model: count generations not years. Compute probability,
of survival of name for ![]() generations.
generations.
Technically easier to compute ![]() , probability of extinction by
generation
, probability of extinction by
generation ![]() .
.
Useful rvs:

| in |
 |
||
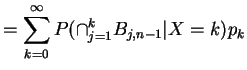 |
||
 |
||
 |

Geometric Distribution: Assume
Then
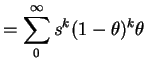 |
||
![$\displaystyle = \theta \sum_0^\infty \left[s(1-\theta)\right]^k$](img87.gif) |
||
 |

One of the roots is 1; the other is

Binomial(![]() ): If
): If
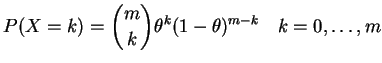
 |
||
Poisson(![]() ): Now
): Now
Important Points: