Example 3: Mean values
![]() = total number of sons in generation
= total number of sons in generation ![]() .
.
![]() for convenience.
for convenience.
Compute
![]() .
.
Recall definition of expected value:
If ![]() is discrete then
is discrete then
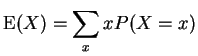
If ![]() is absolutely continuous then
is absolutely continuous then
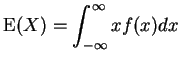
Theorem: If ![]() ,
, ![]() has density
has density ![]() then
then
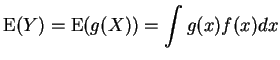
Key properties of ![]() :
:
1: If ![]() then
then
![]() . Equals iff
. Equals iff
![]() .
.
2:
![]() .
.
3: If
![]() then
then
4:
![]() .
.
Conditional Expectations
If ![]() ,
, ![]() , two discrete random variables then
, two discrete random variables then

Extension to absolutely continuous case:
Joint pmf of ![]() and
and ![]() is defined as
is defined as


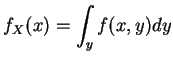
Example:

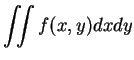 |
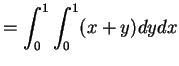 |
|
 |
||
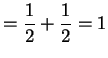 |
The marginal density of ![]() is, for
is, for
![]() .
.
 |
||
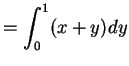 |
||
 |
For ![]() not in
not in ![]() the integral is 0 so
the integral is 0 so
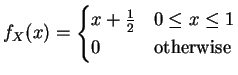
Conditional Densities
If ![]() and
and ![]() have joint density
have joint density
![]() then
we define the conditional density of
then
we define the conditional density of ![]() given
given ![]() by
analogy with our interpretation of densities. We take limits:
by
analogy with our interpretation of densities. We take limits:

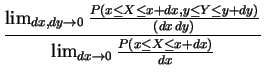
Going back to our interpretation of joint densities and ordinary densities we see that our definition is just

Example: For ![]() of previous example conditional density
of
of previous example conditional density
of ![]() given
given ![]() defined only for
defined only for
![]() :
:

 |
||
 |
||
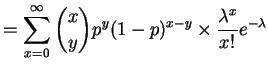 |
WARNING: in sum
![]() is required and
is required and ![]() ,
, ![]() integers
so sum really runs from
integers
so sum really runs from ![]() to
to ![]()
![$\displaystyle = \frac{(p\lambda)^ye^{-\lambda}}{y!} \sum_{x=y}^\infty \frac{\left[(1-p)\lambda\right]^{x-y}}{(x-y)!}$](img60.gif) |
||
![$\displaystyle = \frac{(p\lambda)^ye^{-\lambda}}{y!}\sum_0^\infty \frac{\left[(1-p)\lambda\right]^{k}}{k!}$](img61.gif) |
||
 |
||
Conditional Expectations
If ![]() and
and ![]() are continuous random variables with joint density
are continuous random variables with joint density
![]() we define:
we define:

Key properties of conditional expectation
1: If ![]() then
then
![]() . Equals iff
. Equals iff
![]() .
.
2:
![]() .
.
3: If ![]() and
and ![]() are independent then
are independent then
4:
![]() .
.
Example:


 |
||
 |
Computing expectations by conditioning:
Notation:
![]() is the function of
is the function of ![]() you get by
working out
you get by
working out
![]() , getting a formula in
, getting a formula in ![]() and replacing
and replacing
![]() by
by ![]() . This makes
. This makes
![]() a random variable.
a random variable.
Properties:
1:
![]() .
.
2: If ![]() and
and ![]() are independent then
are independent then
3:
![]() .
.
4:
![]() (compute average
holding
(compute average
holding ![]() fixed first, then average over
fixed first, then average over ![]() ).
).
In example:

For ![]() expect exponential decay. For
expect exponential decay. For ![]() exponential
growth (if not extinction).
exponential
growth (if not extinction).
We have reviewed the following definitions:



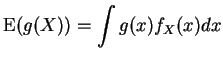

Tactics:

Tactics for expected values: