Monte Carlo computation of expected value:
To compute
![]() : do experiment
: do experiment ![]() times to generate
times to generate
![]() independent observations all with same distribution as
independent observations all with same distribution as
![]() .
.
Get
![]() .
.
Use
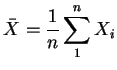
To estimate
![]() : use same
: use same ![]() and compute
and compute

In practice: random quantities are not used.
Use: pseudo-random uniform random numbers.
They ``behave like'' iid Uniform(0,1) variables.
Many, many generators. One standard kind: linear congruential generators.
Start with ![]() an integer in range
an integer in range
![]() .
Compute
.
Compute
Integers ![]() and
and ![]() are chosen so that
are chosen so that
Use

We now pretend we can generate
![]() which are iid Uniform(0,1).
which are iid Uniform(0,1).
Monte Carlo methods for generating a sample:
Fact: ![]() continuous CDF and
continuous CDF and ![]() satisfy
satisfy
Proof: For simplicity: assume ![]() strictly increasing on
inverval
strictly increasing on
inverval ![]() with
with ![]() and
and ![]() .
.
If ![]() Uniform(0,1) then
Uniform(0,1) then
Conversely: if ![]() and
and ![]() then
there is a unique
then
there is a unique ![]() such that
such that ![]()
Application: generate ![]() and solve
and solve ![]() for
for ![]() to get
to get
![]() which has cdf
which has cdf ![]() .
.
Example:For the exponential distribution
Observation:
![]() so
so
![]() also has
an Exponential(
also has
an Exponential(![]() ) distribution.
) distribution.
Example:: for ![]() the standard normal cdf solving
the standard normal cdf solving
Special purpose transformations:
Example:: If ![]() and
and ![]() are iid
are iid ![]() define
define
![]() and
and
![]() by
by
NOTE: Book says

Then
Compute joint cdf of ![]() at
at
![]() .
.
Define

 |

So

Moreover
![]() has cdf
has cdf
![]() is Uniform
is Uniform![]() .
.
So: generate ![]() iid Uniform(0,1).
iid Uniform(0,1).
Define
You have generated two independent ![]() variables.
variables.
If ![]() difficult to solve (eg
difficult to solve (eg ![]() hard
to compute) sometimes use acceptance rejection.
hard
to compute) sometimes use acceptance rejection.
Goal: generate ![]() where
where
![]() .
.
Tactic: find density ![]() and constant
and constant ![]() such that
such that
Algorithm:
Facts:
![$\displaystyle = \int P[U \le f(y)/\{cg(y)\}\vert Y=y]g(y) dy$](img93.gif) |
||
 |
||
 |
||
Most important fact: ![]() :
:
Proof: this is like the old craps example:
We compute
Condition on ![]() to get
to get
![$\displaystyle = \frac{\int_{-\infty}^x P[U \le f(Y)/\{cg(Y)\}\vert Y=y]g(y)dy}{ P[U \le f(Y)/\{cg(Y)\}]}$](img102.gif) |
||
 |
||
 |
||
Example:Half normal distribution: ![]() has density
has density

Use
![]() . To find
. To find ![]() maximize
maximize
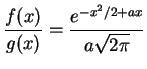

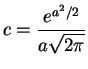
Choose ![]() to minimize
to minimize ![]() (or
(or ![]() ); get
); get
![]() so
so

Algorithm is then: generate
![]() and
then compute
and
then compute
To generate ![]() : use a third
: use a third ![]() to pick a sign
at random: negative if
to pick a sign
at random: negative if ![]() otherwise positive.
otherwise positive.
The inverse transformation method works for discrete distributions.
![]() has possible values
has possible values
![]() with
probabilities
with
probabilities
![]() compute
cumulative probabilities
compute
cumulative probabilities
Generate ![]() Uniform(0,1).
Uniform(0,1).
Find ![]() such that
such that
Put ![]() .
.