Postscript version of this file

STAT 380 Section 9

Brownian Motion

For fair random walk $Y_n$ = number of heads minus number of tails,

$$Y_n = U_1+ \cdots+U_n$$

where the $U_i$ are independent and

$$P(U_i=1) = P(U_i=-1)=\frac{1}{2}$$

Notice:

$${\rm E}(U_i) = 0$$

$${\rm Var}(U_i) = 1$$

Recall central limit theorem:

$$\frac{ U_1+ \cdots+U_n}{\sqrt{n}}\Rightarrow N(0,1)$$

Now: rescale time axis so that $n$ steps take 1 time unit and vertical axis so step size is $1/\sqrt{n}$.

We now turn these pictures into a stochastic process:

For $\frac{k}{n} \le t < \frac{k+1}{n}$ we define

$$X_n(t) = \frac{U_1+\cdots+U_k}{\sqrt{n}}$$

Notice:

$${\rm E}(X_n(t)) = 0$$

and

$${\rm Var}(X_n(t)) = \frac{k}{n}$$

As $n \to \infty$ with $t$ fixed we see $k/n \to t$. Moreover:

$$\frac{U_1+\cdots+U_k}{\sqrt{k}} = \sqrt{\frac{n}{k}} X_n(t)$$

converges to $N(0,1)$ by the central limit theorem. Thus

$$X_n(t) \Rightarrow N(0,t)$$

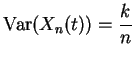
Another observation: $X_n(t+s) -X_n(t)$ is independent of $X_n(t)$ because the two rvs involve sums of different $U_i$.

Conclusions.

As $n \to \infty$ the processes $X_n$ converge to a process $X$ with the properties:

1. $X(t)$ has a $N(0,t)$ distribution.

2. $X$ has independent increments: if
   $$0 = t_0 < t_1 < t_2 < \cdots < t_k$$
   then
   $$X(t_1)-X(t_0), \ldots , X(t_k) - X(t_{k-1})$$
   are independent .

3. The increments are stationary:
   $$X(t+s)-X(s) \sim N(0,t)$$
   regardless of $s$.

4. $X(0)=0$.

Definition:Any process satisfying 1-4 above is a Brownian motion.

Properties of Brownian motion

• Suppose $t>s$. Then

$${\rm E}(X(t)\vert X(s)) = {\rm E}\left\{X(t)-X(s)+X(s)\vert X(s)\right\}$$

$$= {\rm E}\left\{X(t)-X(s)\vert X(s)\right\}$$

$$\qquad + {\rm E}\left\{X(s)\vert X(s)\right\}$$

$$= 0 + X(s) =X(s)$$

Notice the use of independent increments and of ${\rm E}(Y\vert Y)=Y$.

• Again if $t>s$:

  $${\rm Var} \left\{X(t)\vert X(s)\right\}$$

  $$= {\rm Var}\left\{X(t)-X(s)+X(s)\vert X(s)\right\}$$

  $$= {\rm Var}\left\{X(t)-X(s)\vert X(s)\right\}$$

  $$= {\rm Var}\left\{X(t)-X(s)\right\}$$

  $$= t-s$$

  
  

Suppose $t<s$. Then $X(s)=X(t)+\{X(t)-X(s)\}$ is a sum of two independent normal variables. Do following calculation:

$X\sim N(0,\sigma^2)$, and $Y\sim N(0,\tau^2)$ independent. $Z=X+Y$.

Compute conditional distribution of $X$ given $Z$:

$$f_{X\vert Z}(x\vert z) = \frac{f_{X,Z}(x,z)}{f_Z(z)}$$

$$= \frac{ f_{X,Y}(x,z-x)}{f_Z(z)}$$

$$= \frac{ f_X(x)f_Y(z-x)}{f_Z(z)}$$

Now $Z$ is $N(0,\gamma^2)$ where $\gamma^2 = \sigma^2+\tau^2$ so

$$f_{X\vert Z}(x\vert z) = \frac{ \frac{1}{\sigma\sqrt{2\pi}}e^{-x^2/(2\sigma^2)} \frac{1}... ...2\pi}}e^{-(z-x)^2/(2\tau^2)}}{ \frac{1}{\gamma\sqrt{2\pi}}e^{-z^2/(2\gamma^2)}}$$

$$= \frac{\gamma}{\tau\sigma\sqrt{2\pi}} \exp\{-(x-a)^2/(2b^2)\}$$

for suitable choices of $a$ and $b$. To find them compare coefficients of $x^2$, $x$ and $1$.

Coefficient of $x^2$:

$$\frac{1}{b^2} = \frac{1}{\sigma^2}+\frac{1}{\tau^2}$$

so $b= \tau \sigma/\gamma$.

Coefficient of $x$:

$$\frac{a}{b^2} = \frac{z}{\tau^2}$$

so that

$$a=b^2z/\tau^2 = \frac{\sigma^2}{\sigma^2+\tau^2} z$$

Finally you should check that

$$\frac{a^2}{b^2} = \frac{z^2}{\tau^2} -\frac{z^2}{\gamma^2}$$

to make sure the coefficients of $1$ work out as well.

Conclusion: given $Z=z$ the conditional distribution of $X$ is $N(a,b^2)$ with $a$ and $b$ as above.

Application to Brownian motion:

• For $t<s$ let $X$ be $X(t)$ and $Y$ be $X(s)-X(t)$ so $Z=X+Y=X(s)$. Then $\sigma^2 = t$, $\tau^2=s-t$ and $\gamma^2=s$. Thus
  $$b^2 = \frac{(s-t) t}{s}$$
  and
  $$a=\frac{t}{s} X(s)$$
  SO:
  $${\rm E}(X(t)\vert X(s)) = \frac{t}{s} X(s)$$
  and
  $${\rm Var}(X(t)\vert X(s)) = \frac{(s-t) t}{s}$$

The Reflection Principle

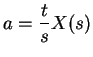
Tossing a fair coin:

HTHHHTHTHHTHHHTTHTH	5 more heads than tails
THTTTHTHTTHTTTHHTHT	5 more tails than heads

Both sequences have the same probability.

So: for random walk starting at stopping time:

Any sequence with $k$ more heads than tails in next $m$ tosses is matched to sequence with $k$ more tails than heads. Both sequences have same prob.

Suppose $Y_n$ is a fair ($p=1/2$) random walk. Define

$$M_n = \max\{Y_k, 0 \le k \le n\}$$

Compute $P(M_n \ge x)$? Trick: Compute

$$P(M_n \ge x, Y_n = y)$$

First: if $y\ge x$ then

$$\{M_n \ge x, Y_n = y\} = \{Y_n = y\}$$

Second: if $M_n \ge x$ then

$$T \equiv \min\{k: Y_k=x\} \le n$$

Fix $y < x$. Consider a sequence of H's and T's which leads to say $T=k$ and $Y_n=y$.

Switch the results of tosses $k+1$ to $n$ to get a sequence of H's and T's which has $T=k$ and $Y_n= x+(x-y)=2x-y>x$. This proves

$$P(T=k, Y_n=y) = P(T=k,Y_n=2x-y)$$

This is true for each $k$ so

$$P(M_n \ge x, Y_n = y) = P(M_n \ge x, Y_n =2x-y)$$

$$= P(Y_n=2x-y)$$

Finally, sum over all $y$ to get

$$P(M_n \ge x) = \sum_{y\ge x} P(Y_n=y)$$

$$\qquad + \sum_{y<x} P(Y_n = 2x-y)$$

Make the substitution $k=2x-y$ in the second sum to get

$$P(M_n \ge x) = \sum_{y\ge x} P(Y_n=y)$$

$$\qquad + \sum_{k>x} P(Y_n=k)$$

$$= 2\sum_{k>x} P(Y_n=k) + P(Y_n=x)$$

Brownian motion version:

$$M_t = \max\{X(s) ; 0 \le s \le t\}$$

$$T_x = \min\{s: X(s)=x\}$$

(called hitting time for level $x$). Then

$$\{T_x \le t\} = \{M_t \ge x\}$$

Any path with $T_x=s <t$ and $X(t)= y<x$ is matched to an equally likely path with $T_x=s <t$ and $X(t)=2x-y>x$.

So for $y>x$

$$P(M_t \ge x, X(t)>y) = P(X(t) > y)$$

while for $y < x$

$$P(M_t \ge x, X(t) < y) = P(X(t) > 2x-y)$$

Let $y\to x$ to get

$$P(M_t \ge x, X(t)>x) = P(M_t \ge x, X(t)<x)$$

$$= P(X(t)>x)$$

Adding these together gives

$$P(M_t > x) = 2P(X(t)>x)$$

$$= 2P(N(0,1)>x/\sqrt{t})$$

Hence $M_t$ has the distribution of $\vert N(0,t)\vert$.

On the other hand in view of

$$\{T_x \le t\} = \{M_t \ge x\}$$

the density of $T_x$ is

$$\frac{d}{dt} 2P(N(0,1)>x/\sqrt{t})$$

Use the chain rule to compute this. First

$$\frac{d}{dy} P(N(0,1)> y) = -\phi(y)$$

where $\phi$ is the standard normal density

$$\phi(y) = \frac{e^{-y^2/2}}{\sqrt{2\pi}}$$

because $P(N(0,1)>y)$ is 1 minus the standard normal cdf.

So

$$\frac{d}{dt} 2P(N(0,1) >x/\sqrt{t})$$

$$= -2 \phi(x/\sqrt{t}) \frac{d}{dt} (x/\sqrt{t})$$

$$= \frac{x}{\sqrt{2\pi}t^{3/2}} \exp\{-x^2/(2t)\}$$

This density is called the Inverse Gaussian density. $T_x$ is called a first passage time

NOTE: the preceding is a density when viewed as a function of the variable $t$.

Martingales

A stochastic process $M(t)$ indexed by either a discrete or continuous time parameter $t$ is a martingale if:

$${\rm E}\{M(t)\vert M(u); 0 \le u \le s\} = M(s)$$

whenever $s<t$.

Examples

• A fair random walk is a martingale.

• If $N(t)$ is a Poisson Process with rate $\lambda$ then $N(t) - \lambda t$ is a martingale.

• Standard Brownian motion (defined above) is a martingale.

Note: Brownian motion with drift is a process of the form

$$X(t) = \sigma B(t) + \mu t$$

where $B$ is standard Brownian motion, introduced earlier. $X$ is a martingale if $\mu=0$. We call $\mu$ the drift

• If $X(t)$ is a Brownian motion with drift then
  $$Y(t) =e^{X(t)}$$
  is a geometric Brownian motion. For suitable $\mu$ and $\sigma$ we can make $Y(t)$ a martingale.

• If a gambler makes a sequence of fair bets and $M_n$ is the amount of money s/he has after $n$ bets then $M_n$ is a martingale - even if the bets made depend on the outcomes of previous bets, that is, even if the gambler plays a strategy.

Some evidence for some of the above:

Random walk: $U_1,U_2,\ldots$ iid with

$$P(U_i=1)=P(U_i=-1) = 1/2$$

and $Y_k=U_1+\cdots+U_k$ with $Y_0=0$. Then

$${\rm E}(Y_n\vert Y_0,\ldots,Y_k)$$

$$= {\rm E}(Y_n-Y_k+Y_k\vert Y_0,\ldots,Y_k)$$

$$= {\rm E}(Y_n-Y_k\vert Y_0,\ldots,Y_k) +Y_k$$

$$= \sum_{k+1}^n {\rm E}(U_j\vert U_1,\ldots,U_k) + Y_k$$

$$= \sum_{k+1}^n {\rm E}(U_j) +Y_k$$

$$= Y_k$$

Things to notice:

$Y_k$ treated as constant given $Y_1,\ldots,Y_k$.

Knowing $Y_1,\ldots,Y_k$ is equivalent to knowing $U_1,\ldots,U_k$.

For $j>k$ we have $U_j$ independent of $U_1,\ldots,U_k$ so conditional expectation is unconditional expectation.

Since Standard Brownian Motion is limit of such random walks we get martingale property for standard Brownian motion.

Poisson Process: $X(t) = N(t) -\lambda t$. Fix $t>s$.

$${\rm E}(X(t) \vert X(u); 0 \le u \le s)$$

$$= {\rm E}(X(t) - X(s)+X(s) \vert {\cal H}_s)$$

$$= {\rm E}(X(t) - X(s)\vert {\cal H}_s) +X(s)$$

$$= {\rm E}(N(t) - N(s) -\lambda(t-s)\vert {\cal H}_s) +X(s)$$

$$= {\rm E}(N(t) - N(s)) -\lambda(t-s) +X(s)$$

$$= \lambda(t-s) -\lambda(t-s)+X(s)$$

$$= X(s)$$

Things to notice:

I used independent increments.

${\cal H}_s$ is shorthand for the conditioning event.

Similar to random walk calculation.

Black Scholes

We model the price of a stock as

$$X(t) = x_0 e^{Y(t)}$$

where

$$Y(t) = \sigma B(t) + \mu t$$

is a Brownian motion with drift ($B$ is standard Brownian motion).

If annual interest rates are $e^\alpha-1$ we call $\alpha$ the instantaneous interest rate; if we invest $1 at time 0 then at time $t$ we would have $e^{\alpha t}$. In this sense an amount of money $x(t)$ to be paid at time $t$ is worth only $e^{-\alpha t} x(t)$ at time 0 (because that much money at time 0 will grow to $x(t)$ by time $t$).

Present Value: If the stock price at time $t$ is $X(t)$ per share then the present value of 1 share to be delivered at time $t$ is

$$Z(t) = e^{-\alpha t} X(t)$$

With $X$ as above we see

$$Z(t) = x_0 e^{\sigma B(t) +(\mu-\alpha)t}$$

Now we compute

$$\begin{multline*} {\rm E}\left\{ Z(t) \vert Z(u);0 \le u \le s\right\} \\ = {\rm E}\left\{ Z(t) \vert B(u);0 \le u \le s\right\} \end{multline*}$$

for $s<t$. Write

$$Z(t) = x_0 e^{\sigma B(s) +(\mu-\alpha)t} \times e^{\sigma(B(t)-B(s))}$$

Since $B$ has independent increments we find

$$\begin{multline*} {\rm E}\left\{ Z(t) \vert B(u);0 \le u \le s\right\} \\ = x_... ...\mu-\alpha)t} \times {\rm E}\left[e^{\sigma\{B(t)-B(s)\}}\right] \end{multline*}$$

Note: $B(t)-B(s)$ is $N(0,t-s)$; the expected value needed is the moment generating function of this variable at $\sigma$.

Suppose $U\sim N(0,1)$. The Moment Generating Function of $U$ is

$$M_U(r) = {\rm E}(e^{rU}) = e^{r^2/2}$$

Rewrite

$$\sigma\{B(t)-B(s)\} = \sigma\sqrt{t-s} U$$

where $U\sim N(0,1)$ to see

$${\rm E}\left[e^{\sigma\{B(t)-B(s)\}}\right]= e^{\sigma^2(t-s)/2}$$

Finally we get

$${\rm E}\{ Z(t) \vert Z(u);0 \le u \le s\}$$

$$= x_0 e^{\sigma B(s) +(\mu-\alpha)s} e^{(\mu-\alpha)(t-s)+\sigma^2(t-s)/2}$$

$$= Z(s)$$

provided

$$\mu+\sigma^2/2=\alpha \, .$$

If this identity is satisfied then the present value of the stock price is a martingale.

Option Pricing

Suppose you can pay $$c$ today for the right to pay $K$ for a share of this stock at time $t$ (regardless of the actual price at time $t$).

If, at time $t$, $X(t) >K$ you will exercise your option and buy the share making $X(t)-K$ dollars.

If $X(t) \le K$ you will not exercise your option; it becomes worthless.

The present value of this option is

$$e^{-\alpha t}(X(t) - K)_+ - c$$

where

$$z_+ = \begin{cases}z& z>0 \\ 0 & z \le 0 \end{cases}$$

(Called positive part of $z$.)

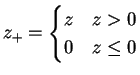
In a fair market:

• The discounted share price $e^{-\alpha t}X(t)$ is a martingale.

• The expected present value of the option is 0.

So:

$$c = {\rm E}\left[ e^{-\alpha t}\left\{X(t) - K\right\}_+\right]$$

Since

$$X(t) = x_0e^{N(\mu t, \sigma^2 t)}$$

we are to compute

$${\rm E}\left\{\left(x_0e^{\sigma t^{1/2} U +\mu t}-K\right)_+\right\}$$

This is

$$\int_a^\infty \left(x_0e^{bu+d}-K \right) e^{-u^2/2} du/\sqrt{2\pi}$$

where

$$a = (\log(K/x_0)-\mu t)/(\sigma t^{1/2})$$

$$b = \sigma t^{1/2}$$

$$d = \mu t$$

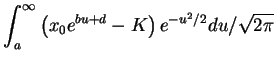
Evidently

$$K \int_a^\infty e^{-u^2/2} du/\sqrt{2\pi} = KP(N(0,1) > a)$$

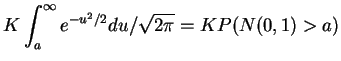
The other integral needed is

$$\int_a^\infty e^{ -u^2/2+bu} du/\sqrt{2\pi}$$

$$= \int_a^\infty \frac{e^{-(u-b)^2/2}e^{b^2/2}}{\sqrt{2\pi}} du$$

$$= \int_{a-b}^\infty \frac{e^{-v^2/2}e^{b^2/2}}{\sqrt{2\pi}} dv$$

$$= e^{b^2/2} P(N(0,1) > a-b)$$

Introduce the notation

$$\Phi(v) = P(N(0,1) \le v) = P(N(0,1) > -v)$$

and do all the algebra to get

$$c = \left\{x_0e^{-\alpha t}e^{b^2/2+d} \Phi(b-a) -Ke^{-\alpha t}\Phi(-a)\right\}$$

$$= \left\{x_0e^{(\mu+\sigma^2/2-\alpha)t}\Phi(b-a) - Ke^{-\alpha t}\Phi(-a)\right\}$$

$$= \left\{x_0\Phi(b-a) - Ke^{-\alpha t}\Phi(-a)\right\}$$

This is the Black-Scholes option pricing formula.