Toss coin 6 times and get Heads twice.
![]() is probability of getting H.
is probability of getting H.
Probability of getting exactly 2 heads is
Definition: The likelihood function is map ![]() : domain
: domain
![]() , values given by
, values given by
Key Point: think about how the density depends on ![]() not
about how it depends on
not
about how it depends on ![]() .
.
Notice: ![]() , observed value of the
data, has been plugged into the formula for density.
, observed value of the
data, has been plugged into the formula for density.
Notice: coin tossing example uses the discrete
density for ![]() .
.
We use likelihood for most inference problems:

Maximum Likelihood Estimation
To find MLE maximize ![]() .
.
Typical function maximization problem:
Set gradient of ![]() equal to 0
equal to 0
Check root is maximum, not minimum or saddle point.
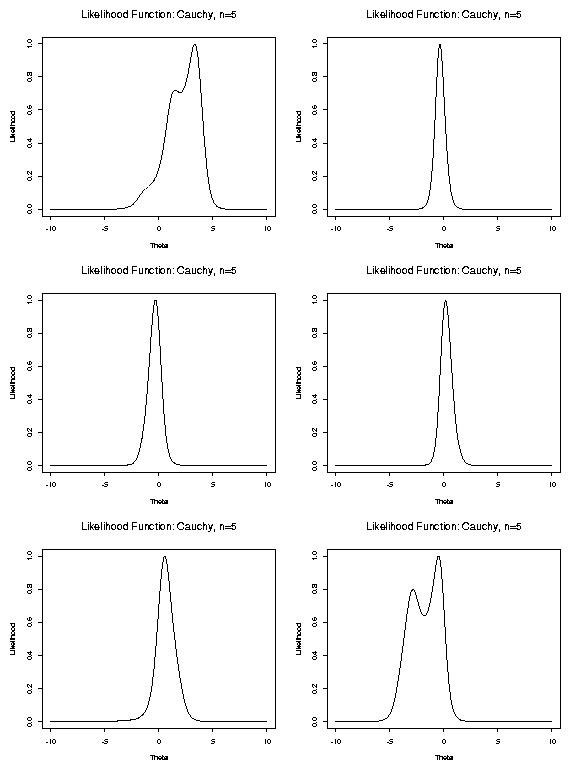
Examine some likelihood plots in examples:
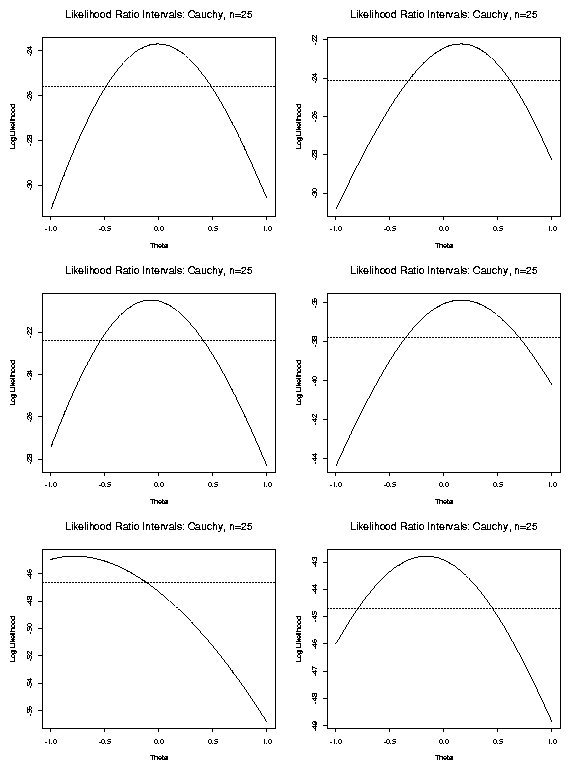
Cauchy Data
Iid sample
![]() from Cauchy
from Cauchy![]() density
density

[Examine likelihood plots.]
 <\CENTER>
<\CENTER>
 <\CENTER>
<\CENTER>
 <\CENTER>
<\CENTER>
 <\CENTER>
I want you to notice the following points:
<\CENTER>
I want you to notice the following points:
To maximize this likelihood: differentiate ![]() ,
set result equal to 0.
,
set result equal to 0.
Notice ![]() is product of
is product of ![]() terms;
derivative is
terms;
derivative is
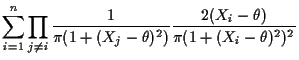
Much easier to work with logarithm
of ![]() : log of product is sum and logarithm is monotone
increasing.
: log of product is sum and logarithm is monotone
increasing.
Definition: The Log Likelihood function is
For the Cauchy problem we have
 <\CENTER>
<\CENTER>
 <\CENTER>
<\CENTER>
 <\CENTER>
<\CENTER>
 <\CENTER>
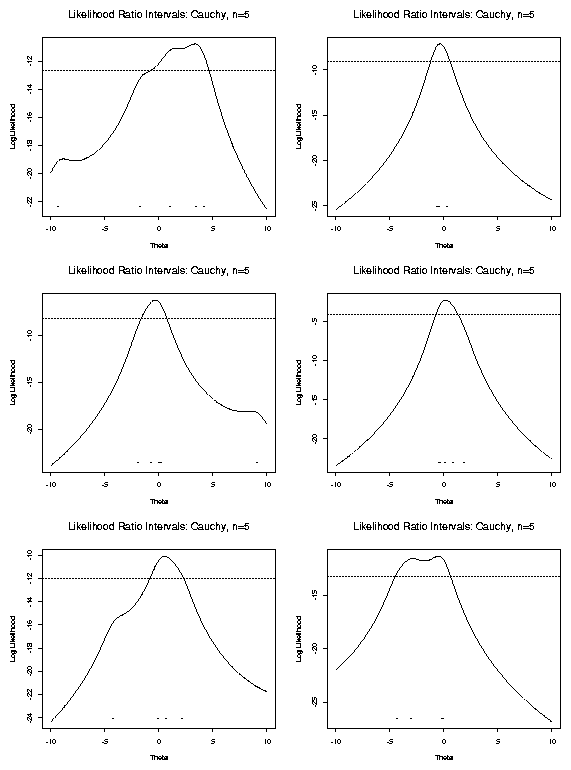
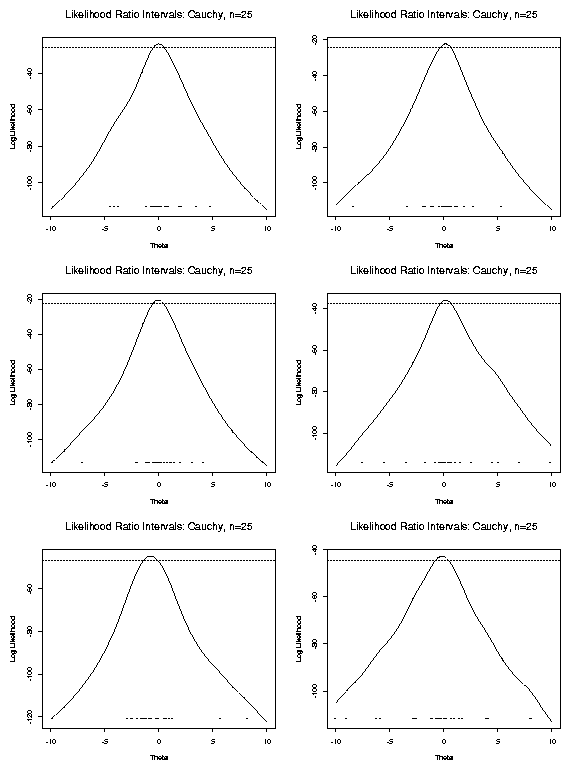
Notice the following points:
<\CENTER>
Notice the following points:
Likelihood tends to 0 as
![]() so max of
so max of ![]() occurs at a root of
occurs at a root of
![]() ,
derivative of
,
derivative of ![]() wrt
wrt ![]() .
.
Def'n: Score Function is gradient of ![]()

MLE
![]() usually root of Likelihood Equations
usually root of Likelihood Equations

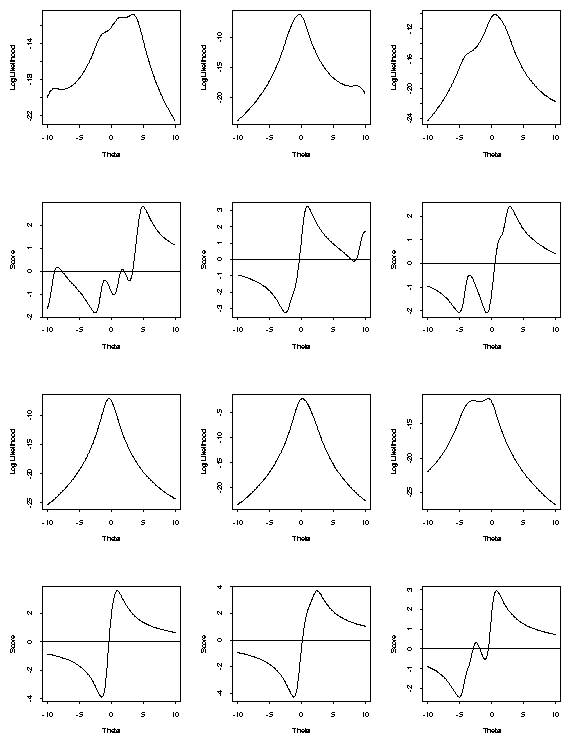
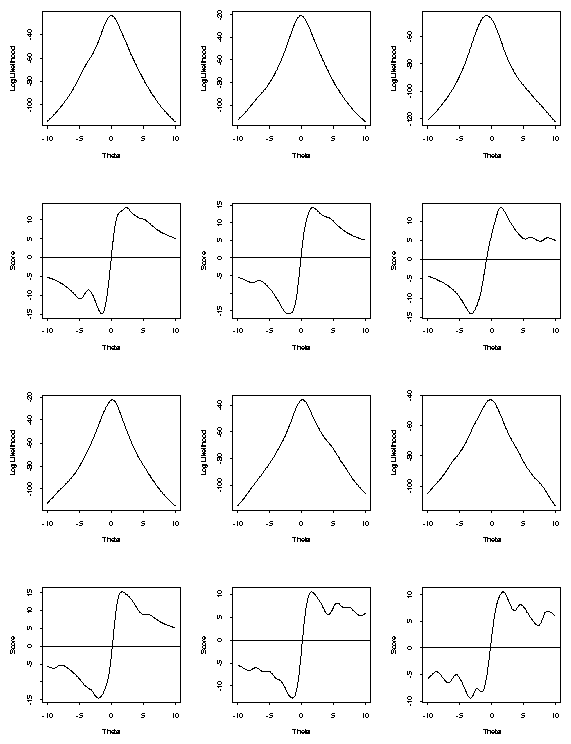
[Examine plots of score functions.]
Notice: often multiple roots of likelihood equations.
 <\CENTER>
<\CENTER>
 <\CENTER>
Example :
<\CENTER>
Example :
 |
||
 |
||
 |

The Normal Distribution
Now we have
![]() iid
iid
![]() . There are
two parameters
. There are
two parameters
![]() . We find
. We find
 |
||
 |
![$\displaystyle \left[ \begin{array}{c}
\frac{\sum(X_i-\mu)}{\sigma^2}
\\
\frac{\sum(X_i-\mu)^2}{\sigma^3} -\frac{n}{\sigma}
\end{array}\right]
$](img65.gif)
Setting the likelihood equal to 0 and solving gives

![$\displaystyle \left[\begin{array}{cc}
\frac{-n}{\sigma^2} & \frac{-2\sum(X_i-\m...
...3} & \frac{-3\sum(X_i-\mu)^2}{\sigma^4}
+\frac{n}{\sigma^2}
\end{array}\right]
$](img69.gif)
![$\displaystyle H(\hat\theta) = \left[\begin{array}{cc}
\frac{-n}{\hat\sigma^2} & 0
\\
0 & \frac{-2n}{\hat\sigma^2}
\end{array}\right]
$](img70.gif)
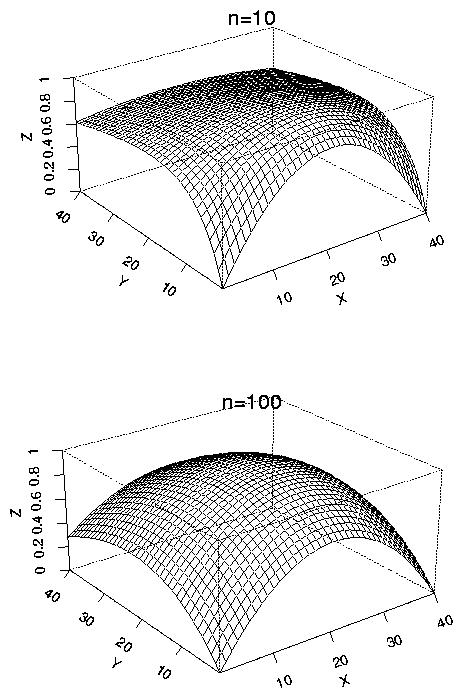
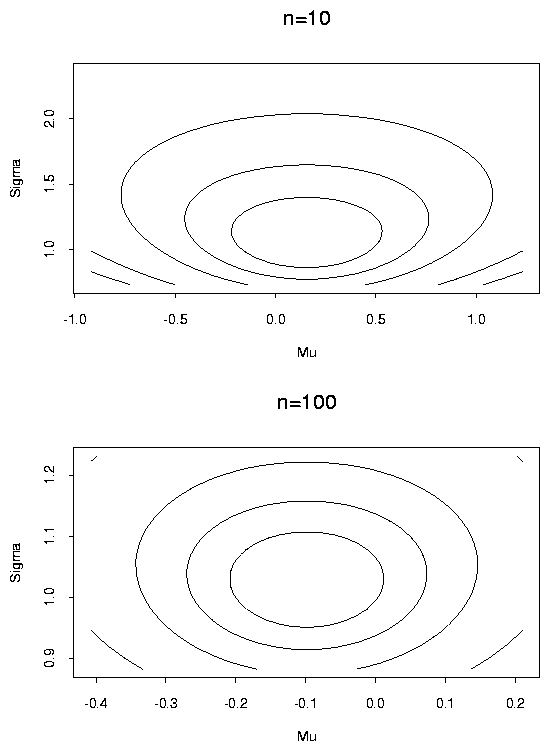
[Examine contour and perspective plots of ![]() .]
.]
 <\CENTER>
<\CENTER>
 <\CENTER>
Notice that the contours are quite ellipsoidal for
the larger sample size.
<\CENTER>
Notice that the contours are quite ellipsoidal for
the larger sample size.
For
![]() iid log likelihood is
iid log likelihood is
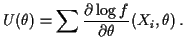
Some examples concerning existence of roots:
N
![]() )
)
Unique root of likelihood equations is a global maximum.
[Remark: Suppose we called
![]() the parameter.
Score function still has two components:
first component same as before but
second component is
the parameter.
Score function still has two components:
first component same as before but
second component is
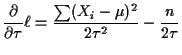
Cauchy: location ![]()
At least 1 root of likelihood equations but often several more. One root is a global maximum; others, if they exist may be local minima or maxima.
Binomial(![]() )
)
If ![]() or
or ![]() : no root of likelihood equations;
likelihood is monotone. Other values of
: no root of likelihood equations;
likelihood is monotone. Other values of
![]() : unique root, a global maximum. Global
maximum at
: unique root, a global maximum. Global
maximum at
![]() even if
even if ![]() or
or ![]() .
.
The 2 parameter exponential
The density is
Three parameter Weibull
The density in question is
![$\displaystyle f(x;\alpha,\beta,\gamma)
= \frac{1}{\beta} \left(\frac{x-\alpha}{\beta}\right)^{\gamma-1}
\exp[-\{(x-\alpha)/\beta\}^\gamma]1(x>\alpha)
$](img92.gif)
Set ![]() derivative equal to 0; get
derivative equal to 0; get
![$\displaystyle \hat\beta(\alpha,\gamma) = \left[\sum (X_i-\alpha)^\gamma/n\right]^{1/\gamma}
$](img93.gif)
However putting
![]() and letting
and letting
![]() will make the log likelihood go to
will make the log likelihood go to ![]() .
.
MLE is not uniquely defined: any
![]() and any
and any ![]() will do.
will do.
If the true value of ![]() is more than 1 then the probability that
there is a root of the likelihood equations is high; in this case there
must be two more roots: a local maximum and a saddle point! For a
true value of
is more than 1 then the probability that
there is a root of the likelihood equations is high; in this case there
must be two more roots: a local maximum and a saddle point! For a
true value of ![]() the theory we detail below applies to the
local maximum and not to the global maximum of the likelihood equations.
the theory we detail below applies to the
local maximum and not to the global maximum of the likelihood equations.