Large Sample Theory
Study approximate behaviour of
![]() by studying
the function
by studying
the function ![]() .
.
Notice ![]() is sum of independent random variables.
is sum of independent random variables.
Theorem: If
![]() are iid with mean
are iid with mean ![]() then
then
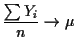
Called law of large numbers. Strong law
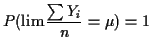
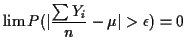
Now suppose ![]() is true value of
is true value of ![]() . Then
. Then
![$\displaystyle E_{\theta_0}\left[ \frac{\partial\log f}{\partial\theta}(X_i,\theta)\right]$](img13.gif) |
||
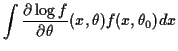 |
Example: ![]() data:
data:
Consider
![]() : derivative of
: derivative of
![]() is likely to be positive so that
is likely to be positive so that ![]() increases
as
increases
as ![]() increases.
increases.
For
![]() : derivative
is probably negative and so
: derivative
is probably negative and so ![]() tends to be decreasing for
tends to be decreasing for
![]() .
.
Hence: ![]() is likely to be maximized close to
is likely to be maximized close to ![]() .
.
Repeat ideas for more general case. Study rv
Generalization: Jensen's inequality:
for ![]() a convex function (
a convex function (
![]() roughly) then
roughly) then
Inequality above has ![]() . Use
. Use
![]() :
convex because
:
convex because
![]() . We get
. We get
![$\displaystyle E_{\theta_0}\left[\frac{f(X_i,\theta)}{f(X_i,\theta_0)}\right]$](img36.gif) |
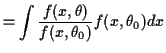 |
|
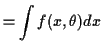 |
||
Let
![]() be this expected value.
be this expected value.
Then
for each ![]() we find
we find
![\begin{multline*}
\frac{\ell(\theta) - \ell(\theta_0)}{n}
\\
=
\frac{\sum \log[f(X_i,\theta)/f(X_i,\theta_0)] }{n}
\\
\to \mu(\theta)
\end{multline*}](img42.gif)
Idea can often be stretched to prove that the mle is consistent.
Definition A sequence
![]() of estimators of
of estimators of
![]() is consistent if
is consistent if
![]() converges weakly
(or strongly) to
converges weakly
(or strongly) to ![]() .
.
Proto theorem: In regular problems the mle
![]() is consistent.
is consistent.
More precise statements of possible conclusions. Use notation
Suppose:
![]() is global maximizer of
is global maximizer of ![]() .
.
![]() maximizes
maximizes ![]() over
over
![]() .
.
Point: conditions get weaker as conclusions get weaker. Many possible conditions in literature. See book by Zacks for some precise conditions.
Study shape of log likelihood near the true
value of ![]() .
.
Assume
![]() is a root of the likelihood equations close to
is a root of the likelihood equations close to ![]() .
.
Taylor expansion (1 dimensional parameter ![]() ):
):
| 0 | ||
WARNING: This form of the remainder in Taylor's theorem is not valid
for multivariate ![]() .
Derivatives of
.
Derivatives of ![]() are sums of
are sums of ![]() terms.
terms.
So each derivative should be proportional
to ![]() in size.
in size.
Second derivative is multiplied by the
square of the small number
![]() so should be
negligible compared to the first derivative term.
so should be
negligible compared to the first derivative term.
Ignoring second derivative term get
Normal case:
Derivative is
Next derivative
![]() is 0.
is 0.
Notice: both ![]() and
and ![]() are
sums of iid random variables.
are
sums of iid random variables.
Let
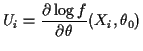
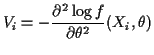
In general,
![]() has mean 0
and approximately a normal distribution.
has mean 0
and approximately a normal distribution.
Here is how we check that:
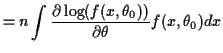 |
||
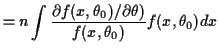 |
||
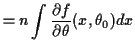 |
||
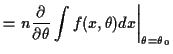 |
||
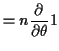 |
||
Notice: interchanged order of differentiation and integration at one point.
This step is usually justified by applying the dominated convergence theorem to the definition of the derivative.
Differentiate identity just proved:
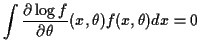
![$\displaystyle \int \frac{\partial}{\partial\theta} \left[
\frac{\partial\log f}{\partial\theta}(x,\theta) f(x,\theta)
\right] dx =0
$](img85.gif)
![\begin{multline*}
-\int\frac{\partial^2\log(f)}{\partial\theta^2} f(x,\theta) dx...
...artial\log f}{\partial\theta}(x,\theta) \right]^2
f(x,\theta) dx
\end{multline*}](img86.gif)
Definition: The Fisher Information is
The idea is that ![]() is a measure of how curved the log
likelihood tends to be at the true value of
is a measure of how curved the log
likelihood tends to be at the true value of ![]() .
Big curvature means precise estimates. Our identity above
is
.
Big curvature means precise estimates. Our identity above
is
Now we return to our Taylor expansion approximation
We have shown that
![]() is a sum of iid mean 0 random variables.
The central limit theorem thus proves that
is a sum of iid mean 0 random variables.
The central limit theorem thus proves that
Next observe that
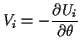
![$\displaystyle n^{1/2} (\hat\theta - \theta_0) \approx
\left[\frac{\sum V_i}{n}\right]^{-1} \frac{\sum U_i}{\sqrt{n}}
$](img97.gif)
Summary
In regular families: assuming
![]() is a consistent
root of
is a consistent
root of
![]() .
.
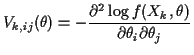
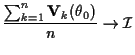
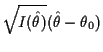 |
||
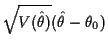 |
Note: If the square roots are replaced by matrix square roots we
can let ![]() be vector valued and get
be vector valued and get ![]() as the limit law.
as the limit law.
Why all these different forms? Use limit
laws to test hypotheses and compute confidence intervals.
Test
![]() using one of the 4 quantities as
test statistic. Find confidence intervals using quantities
as pivots. E.g.: second and fourth limits lead to
confidence intervals
using one of the 4 quantities as
test statistic. Find confidence intervals using quantities
as pivots. E.g.: second and fourth limits lead to
confidence intervals
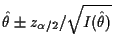
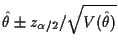
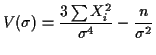
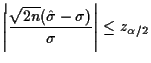
Usual summary: mle is consistent and asymptotically normal with an asymptotic variance which is the inverse of the Fisher information.
Method of Moments
Basic strategy: set sample moments equal to population moments and solve for the parameters.
Definition: The
![]() sample moment (about the origin)
is
sample moment (about the origin)
is
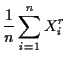
( Central moments are

If we have ![]() parameters we can estimate the parameters
parameters we can estimate the parameters
![]() by solving the system of
by solving the system of ![]() equations:
equations:
Gamma Example
The Gamma(
![]() ) density is
) density is
![$\displaystyle f(x;\alpha,\beta) =
\frac{1}{\beta\Gamma(\alpha)}\left(\frac{x}{\beta}\right)^{\alpha-1}
\exp\left[-\frac{x}{\beta}\right] 1(x>0)
$](img141.gif)
The method of moments equations are much easier to solve than the likelihood equations which involve the function
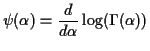
Score function has components
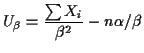
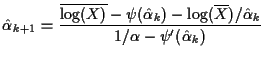
Estimating Equations
Same large sample ideas arise whenever estimates derived by solving some equation.
Example: large sample theory for Generalized Linear Models.
Suppose ![]() is number of cancer cases in some group of people characterized by values
is number of cancer cases in some group of people characterized by values
![]() of some covariates.
of some covariates.
Think of ![]() as containing variables like age, or a dummy for sex or
average income or
as containing variables like age, or a dummy for sex or
average income or ![]() .
.
Possible parametric regression model:
![]() has a Poisson distribution with mean
has a Poisson distribution with mean ![]() where the mean
where the mean
![]() depends somehow on
depends somehow on ![]() .
.
Typically assume
![]() ;
;
![]() is link function.
is link function.
Often
![]() and
and
![]() is a matrix product:
is a matrix product: ![]() row vector,
row vector,
![]() column vector.
column vector.
``Linear regression model with Poisson errors''.
Special case
![]() where
where ![]() is a scalar.
is a scalar.
The log likelihood is simply
Other estimating equations are possible, popular.
If ![]() is any set of
deterministic weights (possibly depending on
is any set of
deterministic weights (possibly depending on ![]() )
then could define
)
then could define
Idea widely used:
Example: Generalized Estimating Equations, Zeger and Liang.
Abbreviation: GEE.
Called by econometricians Generalized Method of Moments.
An estimating equation is unbiased if
Theorem: Suppose
![]() is a consistent root of the
unbiased estimating equation
is a consistent root of the
unbiased estimating equation
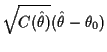 |