![\begin{displaymath}
\Sigma = \left[\begin{array}{rr} \Sigma_{11} & \Sigma_{12} \\
\Sigma_{21} & \Sigma_{22}\end{array}\right]
\end{displaymath}](img5.gif)
- Show that
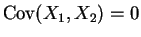 if and only if
if and only if 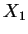 and
and 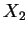 are independent. Use my definition of MVN; you are not allowed
to assume that
are independent. Use my definition of MVN; you are not allowed
to assume that 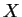 has a density. A mathematically careful argument may
rely on the fact that if
has a density. A mathematically careful argument may
rely on the fact that if
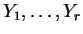 are independent and
are independent and 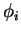 are (measurable) functions then
are (measurable) functions then
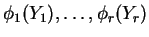 are independent.
are independent.
- Show that whether or not
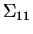 is singular, each column of
is singular, each column of
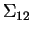 is in the column space of
is in the column space of 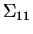 .
.
Hint: one way to do this is to use the following outline.
- Define
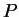 and
and 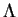 to be the matrix of orthonormal eigenvectors
and the diagonal matrix of corresponding eigenvalues of
to be the matrix of orthonormal eigenvectors
and the diagonal matrix of corresponding eigenvalues of 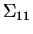 I showed in class. The columns of
I showed in class. The columns of 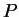 are a basis of
are a basis of 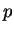 dimensional space
if
dimensional space
if 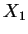 has
has 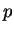 components. You can write any vector
components. You can write any vector 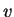 as a linear
combination of the columns of
as a linear
combination of the columns of 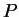 , that is, in the form
, that is, in the form 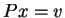 .
.
- Suppose
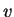 is a column of
is a column of 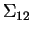 and write
and write
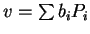 where the
where the 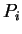 are the columns of
are the columns of 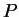 . You are supposed to find an
. You are supposed to find an 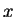 such that
such that
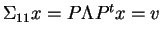 . If
. If
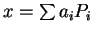 then
use the orthogonality of the
then
use the orthogonality of the 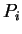 to derive a relationship between
to derive a relationship between
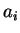 ,
, 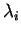 and
and 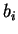 .
.
- If
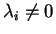 you can solve this for
you can solve this for 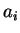 while if
while if
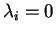 then the relationship in the previous part is true anyway. This gives you
a formula for
then the relationship in the previous part is true anyway. This gives you
a formula for 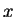 as a linear combination of the
as a linear combination of the 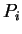 .
.
- Define
- Show that there is a matrix
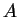 which is
which is 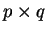 such that
such that
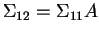 .
.
- Let
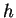 be a column of
be a column of 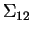 and
and 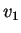 and
and 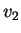 be any vectors
such that
be any vectors
such that
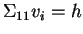 for
for 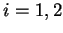 . Show that
. Show that
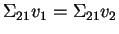 .
.
- Show that if
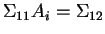 for
for 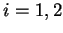 then
then
 .
.
- Show that
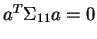 implies
implies
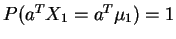 for any
for any 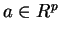 .
.
- Suppose
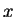 is such that
is such that
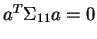 implies
implies
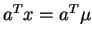 . Show that the conditional distribution
of
. Show that the conditional distribution
of 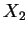 given
given 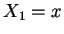 is well-defined and is multivariate
normal with mean
is well-defined and is multivariate
normal with mean
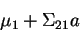
and variance covariance
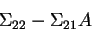
where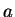 is any solution of
is any solution of
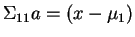 and
and 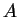 is any solution of
is any solution of
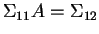 .
.
NOTE: Most facts about
![]() variates
variates ![]() can be demonstrated
by writing
can be demonstrated
by writing ![]() for well chosen
for well chosen ![]() .
.
![\begin{displaymath}
A=\left[\begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right]
\end{displaymath}](img58.gif)
and then find a symmetric square root.
![\begin{displaymath}
\Sigma = \left[\begin{array}{rrr} 2 & 1 & -1 \\ 1 & 1 & -1 \\ -1 & -1 & 1 \end{array}\right]
\end{displaymath}](img61.gif)
Find the conditional distribution of