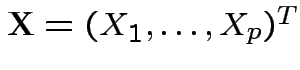 ,
,
Course outline:
Basic structure of typical multivariate data set:
Case by variables: data in matrix. Each row is a case, each column is a variable.
Example: Fisher's iris data: 5 rows of 150 by 5 matrix:
| Case | Sepal | Sepal | Petal | Petal | |
| # | Variety | Length | Width | Length | Width |
| 1 | Setosa | 5.1 | 3.5 | 1.4 | 0.2 |
| 2 | Setosa | 4.9 | 3.0 | 1.4 | 0.2 |
| &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; |
| 51 | Versicolor | 7.0 | 3.2 | 4.7 | 1.4 |
| &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; | &vellip#vdots; |
Vector valued random variable: function
![]() such that,
writing
such that,
writing
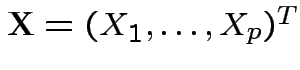 ,
,
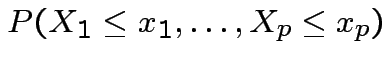
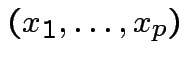 .
.
Cumulative Distribution Function (CDF) of ![]() : function
: function 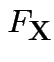 on
on
![]() defined by
defined by
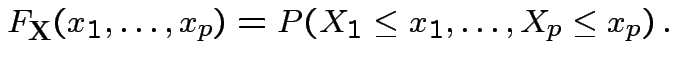
Defn: Distribution of rv ![]() is absolutely continuous
if there is a function
is absolutely continuous
if there is a function ![]() such that
such that
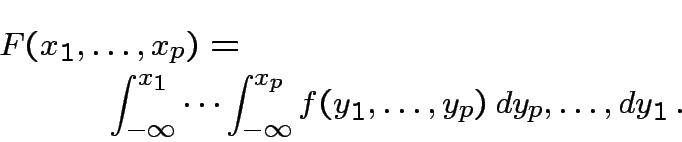
Defn: Any ![]() satisfying (
satisfying (![]() ) is a density of
) is a density of ![]() .
.
For most ![]()
![]() is differentiable at
is differentiable at ![]() and
and
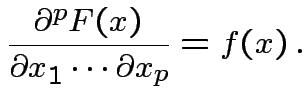
Basic tactic: specify density of

Tools: marginal densities, conditional densities, independence, transformation.
Marginalization: Simplest multivariate problem
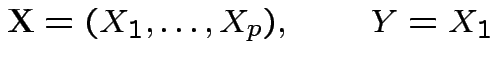
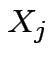 ).
).
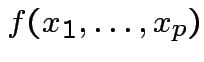 and
and 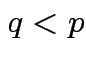 then
then
 has density
has density
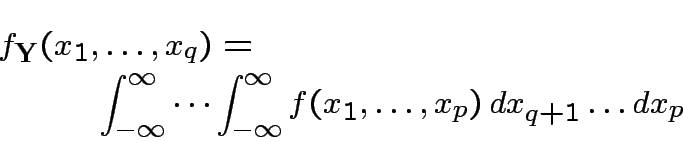
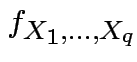 is the marginal density of
is the marginal density of
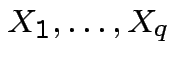 and
and ![]() the joint density of
the joint density of ![]() but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of
but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of ![]() .
.
Def'n: Events ![]() and
and ![]() are independent if
are independent if
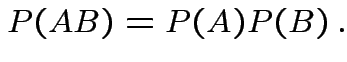
Def'n: ![]() ,
,
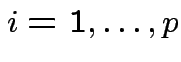 are
independent if
are
independent if
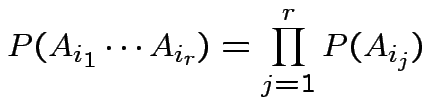
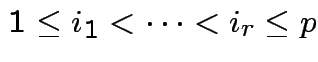 .
.
Def'n: ![]() and
and ![]() are
independent if
are
independent if
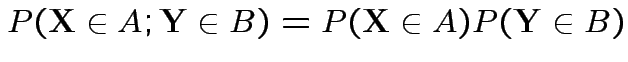
Def'n: Rvs
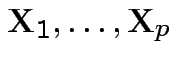 independent:
independent:

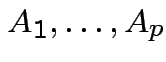 .
.
Theorem:
 then
then 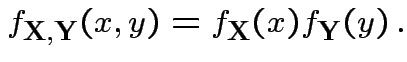
 has joint density
has joint density
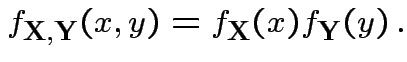
 has density
has density  and there exist
and there exist
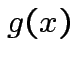 and
and 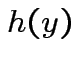 st
st
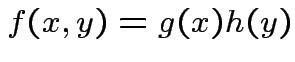 for (almost) all
for (almost) all 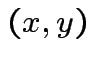 then
then
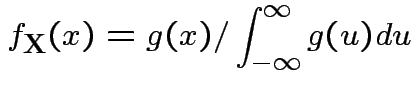
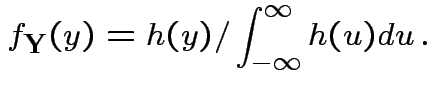
Theorem: If
 are independent and
are independent and
 then
then
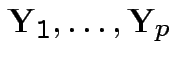 are independent.
Moreover,
are independent.
Moreover,
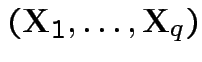 and
and
 are
independent.
are
independent.
Conditional density of ![]() given
given ![]() :
:
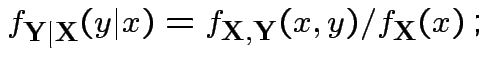
Suppose
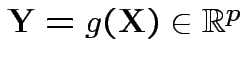 with
with
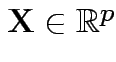 having density
having density ![]() .
Assume
.
Assume ![]() is a one to one (``injective") map, i.e.,
is a one to one (``injective") map, i.e.,
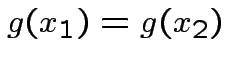 if and only if
if and only if 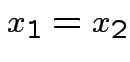 .
Find
.
Find ![]() :
:
Step 1: Solve for ![]() in terms of
in terms of ![]() :
:
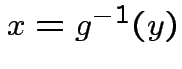 .
.
Step 2: Use basic equation:

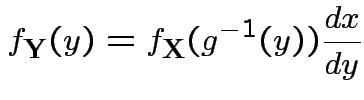
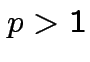 :
:
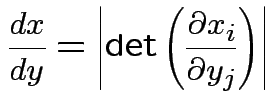
Equivalent formula inverts the matrix:

![$\displaystyle \left\vert\frac{dy}{dx}\right\vert =
\left\vert \mbox{det} \left...
...} & \cdots &
\frac{\partial y_p}{\partial x_p}
\end{array} \right]\right\vert
$](img71.gif)
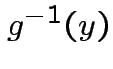 .
.
Example: The density
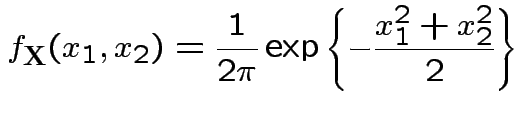
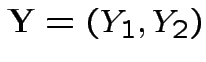 where
where
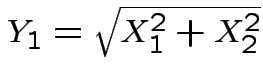 and
and
 is angle
from the positive
is angle
from the positive  .
I.e.,
.
I.e.,
Solve for ![]() in terms of
in terms of ![]() :
:
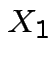 |
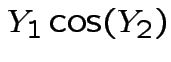 |
||
 |
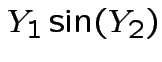 |
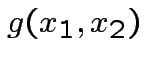 |
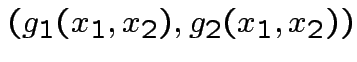 |
||
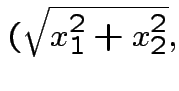 argument argument |
|||
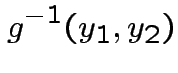 |
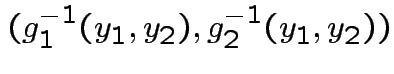 |
||
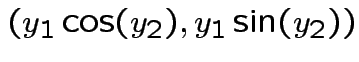 |
|||
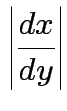 |
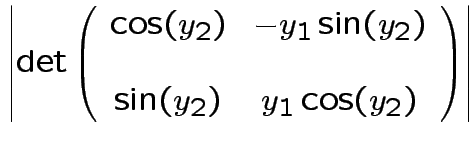 |
||
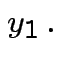 |
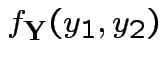 |
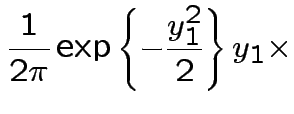 |
||
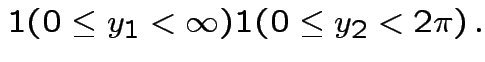 |
Next: marginal densities of ![]() ,
, ![]() ?
?
Factor ![]() as
as
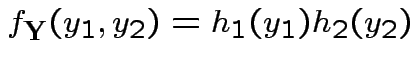 where
where
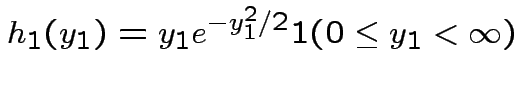

Then
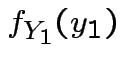 |
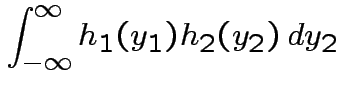 |
||
 |
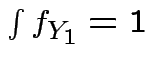 but in this case
but in this case
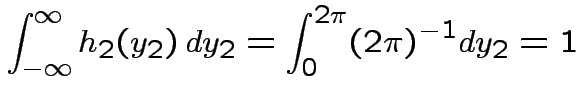
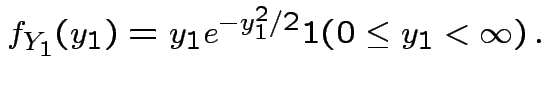
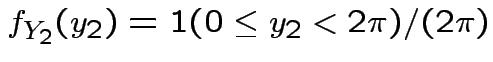
 density.
Exercise:
density.
Exercise: 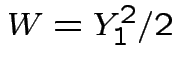 has standard exponential
distribution. Recall: by definition
has standard exponential
distribution. Recall: by definition 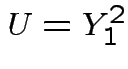 has a
has a
Remark: easy to check
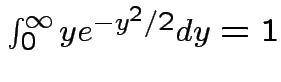 .
.
Thus: have proved original bivariate normal density integrates to 1.
Put
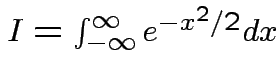 .
Get
.
Get
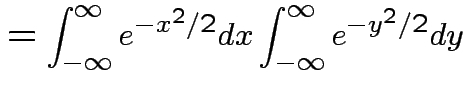 |
||
 |
||
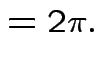 |
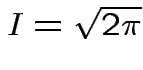 .
.