Definition: Two processes ![]() and
and ![]() are jointly (strictly) stationary
if
are jointly (strictly) stationary
if
Definition: If ![]() is stationary then we call
is stationary then we call
![]() the autocovariance function of
the autocovariance function of ![]() .
.
Definition: If ![]() and
and ![]() are jointly stationary then we call
are jointly stationary then we call
![]() the cross-covariance
function.
the cross-covariance
function.
Notice that
![]() and
and
![]() for all
for all
![]() and similarly for correlation
and similarly for correlation
Definition: The autocorrelation function of ![]() is
is
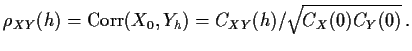
Fact: If ![]() and
and ![]() are jointly stationary then
are jointly stationary then
![]() is stationary for any constants
is stationary for any constants ![]() and
and ![]() .
.
The goal of this section is to develop tools to permit us to
choose a model for a given series ![]() . We will be attempting to
fit an
. We will be attempting to
fit an ![]() and our first step is to learn how to choose
and our first step is to learn how to choose
![]() and
and ![]() . We will try to get small values of these orders and
our efforts are focused on the cases with either
. We will try to get small values of these orders and
our efforts are focused on the cases with either ![]() or
or ![]() equal to
0. We use the autocorrelation or autocovariance function to do model
identification.
equal to
0. We use the autocorrelation or autocovariance function to do model
identification.
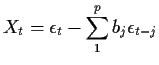
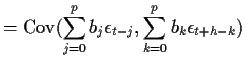 |
||
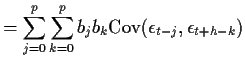 |
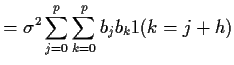 |
||
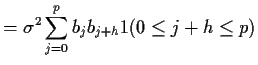 |
||
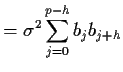 |
Notice that if ![]() (or
(or ![]() ) then we get
) then we get ![]() .
.
Jargon: We call ![]() the lag and say that for
an
the lag and say that for
an ![]() process the autocovariance function is 0 at lags
larger than
process the autocovariance function is 0 at lags
larger than ![]() .
.
To identify an ![]() look at a graph of an
estimate
look at a graph of an
estimate
![]() and look for a lag where it suddenly
decreases to (nearly) 0.
and look for a lag where it suddenly
decreases to (nearly) 0.
For ![]() the term
the term
![]() . This gives
. This gives
Notice that ![]() decreases geometrically to 0 but is never
actually 0.
decreases geometrically to 0 but is never
actually 0.
Remark: If ![]() is small so that
is small so that ![]() is
very small then an
is
very small then an ![]() process is approximately the same
as an
process is approximately the same
as an ![]() process: we nearly have
process: we nearly have
![]() .
.