Definition: If
![]() is a white noise series and
is a white noise series and ![]() and
and
![]() are constants then
are constants then
Question: From observations on ![]() can we estimate the
can we estimate the
![]() 's and
's and
![]() Var
Var![]() accurately? NO.
accurately? NO.
Definition: A model for data ![]() is a family
is a family
![]() of possible distributions for
of possible distributions for ![]() .
.
Definition: A model is identifiable if
![]() implies
that
implies
that
![]() ; that is different
; that is different ![]() 's
give different distributions for the data.
's
give different distributions for the data.
When a model is unidentifiable there are different values of ![]() which make exactly the same predictions about the data so the data
do not permit you to distinguish between these
which make exactly the same predictions about the data so the data
do not permit you to distinguish between these ![]() values.
values.
Example: Suppose ![]() is an iid
is an iid
![]() series and that
series and that
![]() . Then the series
. Then the series ![]() has
mean 0 and covariance
has
mean 0 and covariance
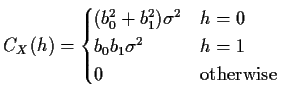
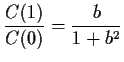

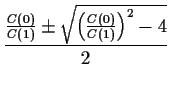
You should notice two things:
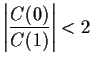

The two solutions multiply together to
give the constant term 1 in the quadratic equation. If the two roots
are distinct it follows that one of them is larger than 1 and the other
smaller in absolute value. Let ![]() and
and ![]() denote the two roots.
Let
denote the two roots.
Let
![]() and
and
![]() . Let
. Let
![]() be
iid
be
iid
![]() and
and
![]() be iid
be iid
![]() . Then
. Then
Reason: We can manipulate the model equation for ![]() just as we did for and autoregressive process last time:
just as we did for and autoregressive process last time:
 |

If, on the other hand, ![]() then we can write
then we can write

 |
||
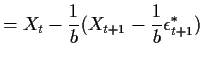 |
||
 |
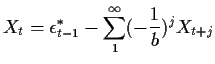
Definition: An ![]() process is invertible if it can be written in the form
process is invertible if it can be written in the form
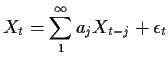
Definition: A process ![]() is an autoregression of order
is an autoregression of order ![]() (written
(written ![]() )
if
)
if
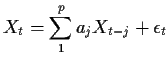
Definition: The backshift operator transforms a time series into another
time series by shifting it back one time unit; if ![]() is a time series
then
is a time series
then ![]() is the time series with
is the time series with
Now we use ![]() to develop a formal method for studying the
existence of a given
to develop a formal method for studying the
existence of a given ![]() and the invertibility of
a given
and the invertibility of
a given ![]() . An
. An ![]() process satisfies
process satisfies
If ![]() is a real number then
is a real number then
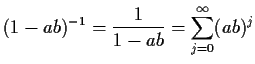


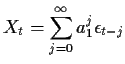
Now consider a general ![]() process:
process:
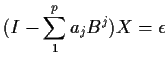

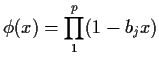


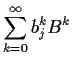
(Asymptotically stationary means this: if you make
![]() anything at all and use the equation defining the
anything at all and use the equation defining the ![]() to define all the rest of the
to define all the rest of the ![]() values then as
values then as
![]() the process
gets closer to being stationary. The assertion of asymptotic stationarity
is equivalent here to the existence of an exactly stationary solution
of the equations.)
the process
gets closer to being stationary. The assertion of asymptotic stationarity
is equivalent here to the existence of an exactly stationary solution
of the equations.)
Definition: A process ![]() is an
is an ![]() (mixed autoregressive of order
(mixed autoregressive of order ![]() and moving average of order
and moving average of order ![]() ) if it satisfies
) if it satisfies
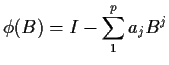
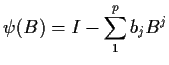
The ideas we used above can be stretched to show that the process ![]() is
identifiable and causal (can be written as an infinite order
autoregression on the past) if the roots of
is
identifiable and causal (can be written as an infinite order
autoregression on the past) if the roots of ![]() lie outside the
unit circle. A stationary solution, which can be written as an infinite
order causal (no future
lie outside the
unit circle. A stationary solution, which can be written as an infinite
order causal (no future ![]() s in the average) moving average, exists
if all the roots of
s in the average) moving average, exists
if all the roots of ![]() lie outside the unit circle.
lie outside the unit circle.
Other Stationary Processes:
| Cov |
||
A Poisson process is a process ![]() indexed by subsets
indexed by subsets ![]() of the
real line with the property that each
of the
real line with the property that each ![]() has a Poisson distribution
with parameter
has a Poisson distribution
with parameter
![]() length
length![]() and if
and if
![]() are any non-overlapping subsets of
are any non-overlapping subsets of ![]() then
then
![]() are independent. We often use
are independent. We often use ![]() for
for
![]() .
.
To define a shot noise process we let ![]() at those
at those ![]() where
there is a jump in
where
there is a jump in ![]() and 0 elsewhere. The process
and 0 elsewhere. The process ![]() is stationary.
If we have some function
is stationary.
If we have some function ![]() defined on
defined on
![]() and decreasing
sufficiently quickly to 0 (like say
and decreasing
sufficiently quickly to 0 (like say
![]() ) then the process
) then the process
