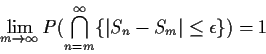Standard approaches to probability theorems:
Event that Yn converges to
0 is
Not explicitly written in terms of simple events involving only a finite number of Ys.
Recall basic definition of
limit: yn converges to 0 if
![]()
![]() such that
such that
![]() we have
we have
![]() .
.
Convert the definition in A into set theory notation:
We get
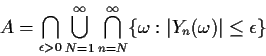
Not obvious A is event because intersection
over
![]() is uncountable.
is uncountable.
However, the intersection is countable. Let

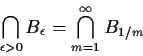
Here are some other events:
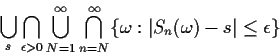
Cauchy sequence:
![]()
![]() such that
such that
![]() we have
we have
![]() .
.
![]() is
is
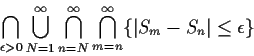

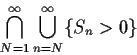

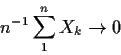
Must prove P(A)=1 where
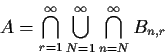
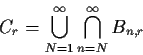
Remark: Usually ``for every
![]() '' will be decreasing intersections
because the condition in the definition is harder to satisfy for
smaller
'' will be decreasing intersections
because the condition in the definition is harder to satisfy for
smaller ![]() .
Similarly unions in definitions tend to be
increasing.
.
Similarly unions in definitions tend to be
increasing.
Now each Cr is an increasing union. Let
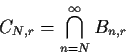
Proof with 4 moments using Borel-Cantelli Lemma.
Suppose An is a sequence of events.
The event
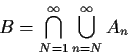
Lemma [Borel-Cantelli]:
If
![]() then
then
![]() .
.
To prove the lemma we need to prove that
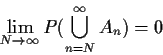
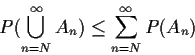
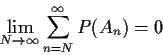
Apply lemma: notice that complement of
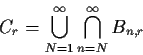
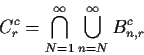
Summary: if we prove
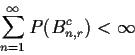
Next ingredient: Markov's inequality
![\begin{align*}P(B_{n,r}^c) & = P(\vert X_1+\cdots+X_n\vert > n/r)
\\
& \le \frac{{\rm E}\left[(X_1+\cdots+X_n)^4\right]}{(n/r)^4}
\end{align*}](img65.gif)
Expand out, collect terms:
![\begin{multline*}{\rm E}\left[(X_1+\cdots+X_n)^4\right]
\\
= n{\rm E}(X_1^4) + n(n-1)\left[{\rm E}(X_1^2)\right]^2
\end{multline*}](img66.gif)
This produces the bound (using
![]() )
)
![\begin{displaymath}P(B_{n,r}^c) \le \frac{r^4{\rm E}(X_1^4)}{n^3} + \frac{r^4\left[{\rm E}(X_1^2)\right]^2}{n^2}
\end{displaymath}](img68.gif)
Assume
![]() .
.
Use Kronecker's Lemma to find event inside A with probability 1.

Lemma implies that

We compute
![]() so study
so study
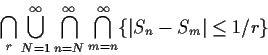
Key ingredient: lower bound on


Now Sm-Sn is a sum of m-n independent rvs. Need
bound on

Theorem [Kolmogorov]:
Suppose
![]() are independent random variables
with finite variances and mean 0. Put
are independent random variables
with finite variances and mean 0. Put
![]() .
Then
.
Then
The proof uses the idea of a stopping time. Define T to be
the least value of
![]() for which
for which
![]() if such a k exists and T=n if no such k exists. Notice
that the event T=k is determined by the variables
if such a k exists and T=n if no such k exists. Notice
that the event T=k is determined by the variables
![]() ;
that is, there is a function
;
that is, there is a function
![]() such that
such that
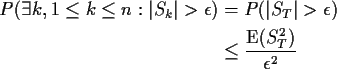
Next we compare
![]() to
to
![]() .
We have
.
We have
![\begin{align*}{\rm E}(S_n^2) & = {\rm E}\left[(S_n-S_T+S_T)^2\right]
\\
& = {\r...
...S_n-S_T)^2\right]
\\
& \qquad + 2{\rm E}\left[S_T(S_n-S_T)\right]
\end{align*}](img96.gif)
First two terms non-negative so if
But
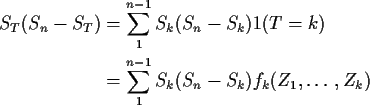
Notice that Sn-Sk and
![]() are independent so
are independent so
![\begin{align*}{\rm E}\left[S_T(S_n-S_T)\right] & = \sum_1^{n-1} {\rm E}(S_n-S_k)
\\
\qquad \times{\rm E}\left[S_k1(T=k)\right]
\\
& = 0
\end{align*}](img100.gif)
Remark: In fact all I needed to prove Kolmogorov's inequality
was to know that Sn-Sk was uncorrelated with
any function of
![]() (or equivalently uncorrelated
with any function of
(or equivalently uncorrelated
with any function of
![]() ).
).
A sequence
![]() is a martingale
if, for each
is a martingale
if, for each ![]() ,
,
(I have yet to define conditional expectation properly but another
definition is that
Theorem [Kolmogorov]:
Suppose
![]() is a martingale
with finite variances and mean 0.
Then
is a martingale
with finite variances and mean 0.
Then
Back to strong law. Fix
![]() and integer m.
The events
and integer m.
The events
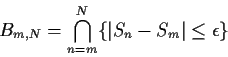
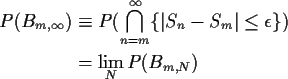
Now
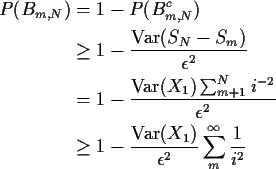
This shows