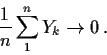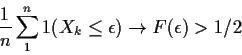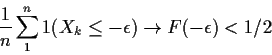Postscript version of this file
STAT 870 Lecture 6
Consistency of MLE
Suppose
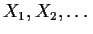 are iid with density
are iid with density
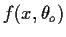 where
where
is a family of densities.
Conditions under which MLE of 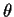 is a.s.
consistent?
is a.s.
consistent?
Goal: find conditions under which
where
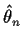 is the mle.
is the mle.
General technical problems:
- What is the precise definition of
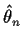 ?
?
- Having settled on some definition is the resulting
object a random variable?
Example: Cauchy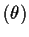 density is
density is
For a sample
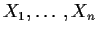 the likelihood is
the likelihood is
We ``define''
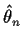 to be the value of
to be the value of 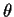 which maximizes this function of
which maximizes this function of 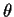 .
.
This is supposed to define
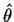 as a function of
as a function of
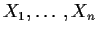 .
.
Underlying supposition: for each
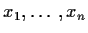
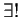
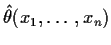 which maximizes the likelihood. If this were so we would have a
definition of a function from
which maximizes the likelihood. If this were so we would have a
definition of a function from
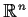 to
to  .
Useful tool: log-likelihood:
.
Useful tool: log-likelihood:
Problems:
- 1.
- Is there, for every
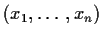 a
a 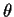 which
maximizes
which
maximizes 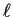 ?
?
- 2.
- If so is the
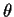 unique?
unique?
- 3.
- If so is
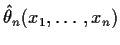 a Borel function
of
a Borel function
of
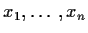 ?
?
Question 1: For the Cauchy density there is always a
maximizer. Fix
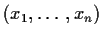 .
As
.
As
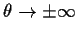 it
is easy to check that
it
is easy to check that
There is then a M such that
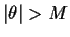 implies
implies
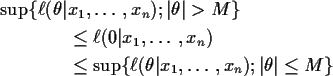
Now the function
is continuous so that it assumes its maximum over
[-M,M]. This shows the existence of at least one
maximizing 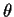 for any set of x values.
for any set of x values.
Question 2: n=2,
x1=x=-x2:
is an even function of x. Derivative
At  this is 0 so
this is 0 so 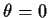 is
critical point of
is
critical point of 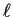 .
2nd derivative may
at 0 is
.
2nd derivative may
at 0 is
If |x| <1 this is negative so that 0 is a local maximum but
if |x| > 1 it is a local minimum. In this case, since 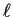 is even there must be two maxima n either side of 0. Note
that putting the two terms in
is even there must be two maxima n either side of 0. Note
that putting the two terms in
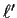 on a common
denominator will give a numerator which is a multiple of
on a common
denominator will give a numerator which is a multiple of
Notice there are exactly three roots if x2>1.
Summary: defining
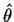 to be the maximizer of
to be the maximizer of
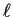 does not actually define a function.
does not actually define a function.
Alternative strategies:
1: You might pick one of the maximizing 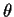 values in an unequivocal way:
values in an unequivocal way:
(The set of such 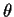 is not empty and bounded so there
is such a
is not empty and bounded so there
is such a
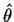 and that
and that
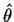 is finite. By
continuity of
is finite. By
continuity of 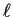
2: You might try defining
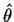 to be
a suitably chosen critical point of
to be
a suitably chosen critical point of 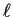 .
.
3: You might try to prove that

In other words it might be true that the set of 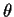 where
where 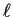 achieves its maximum is almost surely a singleton when the xs are
actually a data set.
achieves its maximum is almost surely a singleton when the xs are
actually a data set.
I am going to follow method 2 since this is the one which
works most generally.
For
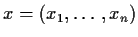 we define the order statistics
we define the order statistics
be the entries in x sorted into non-decreasing order.
If n=2m-1 is odd set
If n=2m set
Now define
Lemma 1
If
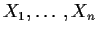
are iid from a distribution
F with the properties:
- 1.
- F(0)=1/2.
- 2.
- For each
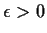
Then
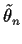
converges almost surely to 0.
Remark: Part of the theorem is that
is an event. Proof:
- A is an event if each
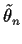 is a random variable.
is a random variable.
- Since the Xi are random variables, we need only check that
gn is Borel.
- This reduces to the assertion that
is Borel for each k and n.
- But

- Sum of Borel functions is Borel so prove
map
is Borel for each t and i.
- This is equivalent to
is Borel.
- This set is open so Borel.
Now to prove the lemma we begin by formalizing an argument we have
used several times.
Lemma 2
Suppose
Yn is a sequence of random variables. Then

almost surely is equivalent to
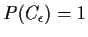
for
each
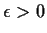
where
Fix
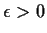 .
For each x rvs
.
For each x rvs
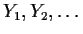 defined by
defined by
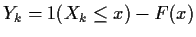 are iid
with mean 0. According to SLLN
there is a null set Nx such that for all
are iid
with mean 0. According to SLLN
there is a null set Nx such that for all
 we
have
we
have
Let
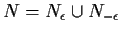 .
Then N is a null set.
If
.
Then N is a null set.
If
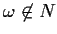 then
then
and
For any such 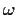 there is an M such that for all
there is an M such that for all 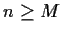 the number of Xi exceeding
the number of Xi exceeding 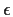 is less than n/2 and
the number of Xi less than
is less than n/2 and
the number of Xi less than 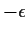 is less than n/2.
Thus for such
is less than n/2.
Thus for such 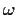 ,
and
,
and 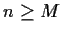
In other words the set
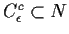 so
so
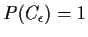 .
.



Richard Lockhart
2000-10-03
![]() are iid with density
are iid with density
![]() where
where
![]() is a.s.
consistent?
is a.s.
consistent?
![]() density is
density is
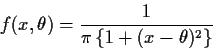
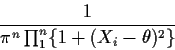
![]() as a function of
as a function of
![]() .
.
![]()
![]()
![]() which maximizes the likelihood. If this were so we would have a
definition of a function from
which maximizes the likelihood. If this were so we would have a
definition of a function from
![]() to
to ![]() .
Useful tool: log-likelihood:
.
Useful tool: log-likelihood:
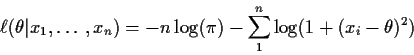
![]() .
As
.
As
![]() it
is easy to check that
it
is easy to check that
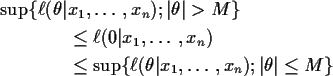
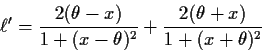
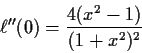
![]() to be the maximizer of
to be the maximizer of
![]() does not actually define a function.
does not actually define a function.
![]() values in an unequivocal way:
values in an unequivocal way:
![]() to be
a suitably chosen critical point of
to be
a suitably chosen critical point of ![]() .
.

![]() where
where ![]() achieves its maximum is almost surely a singleton when the xs are
actually a data set.
achieves its maximum is almost surely a singleton when the xs are
actually a data set.
![]() we define the order statistics
we define the order statistics

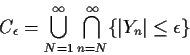
![]() .
For each x rvs
.
For each x rvs
![]() defined by
defined by
![]() are iid
with mean 0. According to SLLN
there is a null set Nx such that for all
are iid
with mean 0. According to SLLN
there is a null set Nx such that for all
![]() we
have
we
have