STAT 870 Lecture 16
Kolmogorov's Equations
The Chapman-Kolmogorov equations are
Subtract 
from both sides, divide by h and let 
.
Remember that 
is the identity.
We find
which gives
The Chapman-Kolmogorov equations can also be written
Now subtracting from both sides, dividing by h and letting
gives
Look at these equations in component form:
becomes
For 
our calculations of instantaneous transition
rates gives
For i = k we have
(X(h)=i either means 
which has probability
or there have been two or more transitions in
[0,h], a possibility of probability o(h).)
Thus
Let 
be the matrix with entries
is the infinitesimal generator of the chain.
Thus
becomes
Called Kolmogorov's backward equations.
On the other hand
becomes
These are Kolmogorov's forward equations.
Remark: When the state space is infinite the forward equations may not be justified. In deriving them we interchanged a limit with an infinite sum; the interchange is always justified for the backward equations but not for forward.
Example: 
. Then
and the chain is otherwise specivied by 
and 
. The matrix
is
The backward equations become
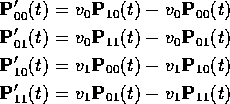
while the forward equations are
Add first and third backwward equations to get
so
Put t=0 to get 
. This gives
Plug this back in to the first equation and get
Multiply by 
and get
which can be integrated to get
Alternative calculation:
can be written as
where
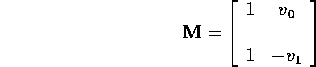
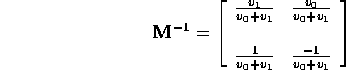
and
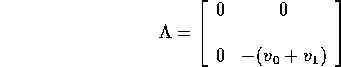
Then
Now
so we get
where
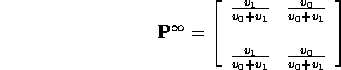
Notice: rows of 
are a stationary initial distribution. If rows are
then
so
Moreover
Fact: 
is long run fraction of time in
state 0.
Fact:
Ergodic Theorem in continuous time.
Potential Pathologies
Suppose that for each k you have a sequence
such that all 
are independent exponential random variables
and has rate parameter 
. We can use these times to
make a Markov chain with state space 
:
Start the chain in state 1. At time 
move to 2, then at 
move
to 3 and so on. The chain progresses through the states in order 1,2, 
.
We have
and
Does this define a process?
Depends on 
.
Case 1: if 
then
(converse to Borel Cantelli) and our construction defines a process X(t) for all t.
Case 2: if 
then
for each k
In this case put 
.
Our definition above defines a process X(t) for 
.
We put 
and then begin the process over with the set
of holding times 
. This defines X for 
.
Again we put 
and continue the process.
Result: X is a Markov Chain with specified transition rates.
Problem: what if we put 
and continued?
What if we used probability vector 
to pick
a value for 
and continued?
All yield Markov Processes with the same infinitesimal generator
.
Birth and Death Processes
Consider a population of X(t) individuals. Suppose
in next time interval (t,t+h) probability of population
increase of 1 (called a birth) is 
and
probability of decrease of 1 (death) is 
.
Jargon: X is a birth and death process.
Special cases:
All 
; called a pure birth process.
All 
(0 is absorbing): pure death process.
and 
is a linear
birth and death process.
, 
: Poisson Process.
and is a linear
birth and death process with immigration.
Queuing Theory
Ingredients of Queuing Problem:
1: Queue input process.
2: Number of servers
3: Queue discipline: first come first serve? last in first out? pre-emptive priorities?
4: Service time distribution.
Example:
Imagine customers arriving at a facility at times of a Poisson
Process N with rate 
. This is the input process,
denoted M (for Markov) in queuing literature.
Single server case:
Service distribution: exponential service times, rate 
.
Queue discipline: first come first serve.
X(t) = number of customers in line at time t.
X is a Markov process called M/M/1 queue:
Example: 
queue:
Customers arrive according to PP rate . Each
customer begins service immediately. X(t) is number
being served at time t. X is a birth and death process
with
and
