Postscript version of this file

STAT 870 Lecture 15

Continuous Time Markov Chains

Consider a population of single celled organisms in a stable environment.

Fix short time interval, length h.

Each organism has some probability of dividing to produce two organisms and some other probability of dying.

We might suppose:

• Different organisms behave independently.
• Probability of division (for specified organism) is plus o(h).
• Probability of death is plus o(h).
• Probability that an organism divides twice (or divides once and dies) in the interval of length h is o(h).

Notice tacit assumption: constants of proportionality do not depend on time (that is our interpretation of ``stable environment'').

Notice too that we have taken the constants not to depend on which organism we are talking about. We are really assuming that the organisms are all similar and live in similar environments.

Y(t): total population at time t.

: history of the process up to time t.

We generally take

General definition of a history (alternative jargon filtration): any family of -fields indexed by t satisfying:

• s ;SPMlt; t implies .
• Y(t) is a measurable random variable.
• .

The last assumption is a technical detail we will ignore from now on.

Condition on event Y(t) =n .

Then the probability of two or more divisions (either more than one division by a single organism or two or more organisms dividing) is o(h) by our assumptions.

Similarly the probability of both a division and a death or of two or more deaths is o(h).

So probability of exactly 1 division by any one of the n organisms is .

Similarly probability of 1 death is .

We deduce:

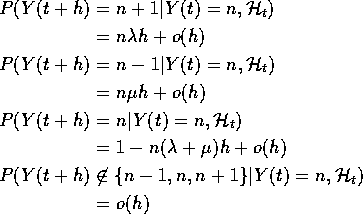
These equations lead to:

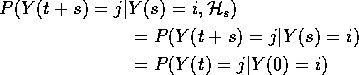
This is the Markov Property.

Definition: A process taking values in S, a finite or countable state space is a Markov Chain if

Definition: A Markov chain Y has stationary transitions if

From now on: our chains have stationary transitions.

Summary of Markov Process Results

• Chapman-Kolmogorov equations:

  

• Exponential holding times: starting from state i time, , until process leaves i has exponential distribution, rate denoted .
• Sequence of states visited, is Markov chain - transition matrix has . Y sometimes called skeleton.
• Communicating classes defined for skeleton chain. Usually assume chain has 1 communicating class.
• Periodicity irrelevant because of continuity of exponential distribution.

• Instantaneous transition rates from i to j:

  

• Kolmogorov backward equations:

  

• Kolmogorov forward equations:

  

• For strongly recurrent chains with a single communicating class:

  

• Stationary initial probabilities satisfy:

  

• Transition probabilities given by

  

  where has entries

  

• Process is a Birth and Death process if

  

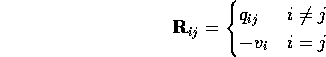
  In this case we write for the instantaneous ``birth'' rate:

  

  and for the instantaneous ``death'' rate:

  

  We have

  

• If all then process is a pure birth process. If all a pure death process.
• Birth and Death process have stationary distribution

  

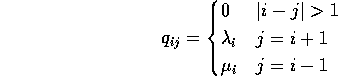
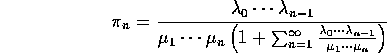
  Necessary condition for existence of is

  

• Linear birth and death processes have

  

  In this case

  

  provided .

Detailed development

Suppose X a Markov Chain with stationary transitions. Then

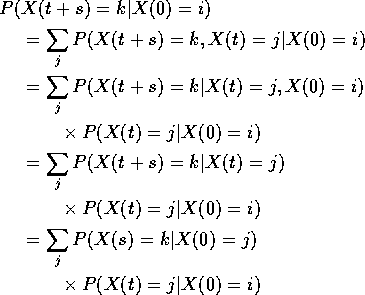
This shows

which is the Chapman-Kolmogorov equation.

Now consider the chain starting from i and let be the first t for which . Then is a stopping time.

[Technically:

for each t.] Then

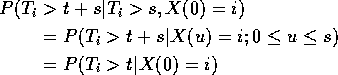
by the Markov property. Note: we actually are asserting a generalization of the Markov property: If f is some function on the set of possible paths of X then

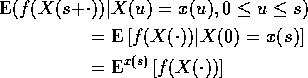
The formula requires some sophistication to appreciate. In it, f is a function which associates a sample path of X with a real number. For instance,

is such a functional. Jargon: functional is a function whose argument is itself a function and whose value is a scalar.

FACT: Strong Markov Property - for a stopping time T

with suitable fix on event .

Conclusion: given X(0)=i, has memoryless porperty so has an exponential distribution. Let be the rate parameter.

Embedded Chain: Skeleton

Let be the stopping times at which tranisitons occur. Then . The sequence is a Markov chain by the strong Markov property. That reflects the fact that by design.

As before we say if for some t. It is fairly clear that for the X(t) if and only if for the embedded chain .

We say if and .

Now consider

Suppose the chain has made n transitions so far so that . Then the event X(t+h)=j is, except for possibilities of probability o(h) the event that

The probability of this is