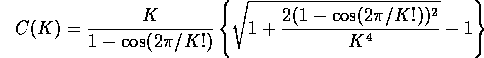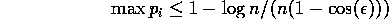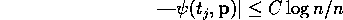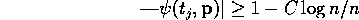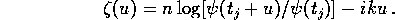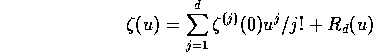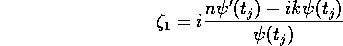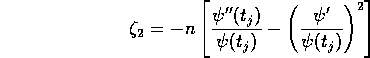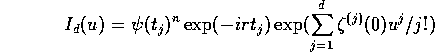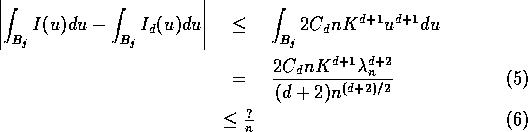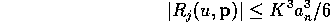A local limit theorem



Next: Consistency of the
Up: Maximum likelihood estimation of
Previous: The offspring distribution
The usual local central limit theorem provides an approximation for the
probability 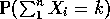 for an iid sequence
for an iid sequence  .
The approximation is proportional to the
lattice size of the underlying distribution of the
.
The approximation is proportional to the
lattice size of the underlying distribution of the  and is not a
continuous function of the underlying distribution. The probability
in question is a continuous function of this underlying
distribution and so the approximation cannot be good uniformly in the class of
possible distributions for the
and is not a
continuous function of the underlying distribution. The probability
in question is a continuous function of this underlying
distribution and so the approximation cannot be good uniformly in the class of
possible distributions for the  . Approximate likelihood methods demand
uniform approximations; in this section we provide such an approximation.
We are unable to handle the case of distributions nearly concentrated on a
single point gracefully. Moreover, it is convenient to impose the stringent
hypothesis that all distributions studied be supported on a fixed finite
set of indices
. Approximate likelihood methods demand
uniform approximations; in this section we provide such an approximation.
We are unable to handle the case of distributions nearly concentrated on a
single point gracefully. Moreover, it is convenient to impose the stringent
hypothesis that all distributions studied be supported on a fixed finite
set of indices 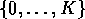 for some fixed
for some fixed 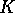 . Fix
. Fix  and let
and let 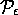 be the set of all probability distributions
be the set of all probability distributions
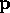 supported on the integers such that
supported on the integers such that 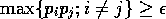 and such that
and such that  for
for 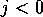 and
and 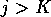 . The conditions
guarantee that the variance
. The conditions
guarantee that the variance 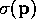 (where it seems convenient we
indicate explicitly the dependence of the mean and variance on the underlying
distribution in question) of the distribution
(where it seems convenient we
indicate explicitly the dependence of the mean and variance on the underlying
distribution in question) of the distribution 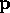 is bounded
away from
is bounded
away from  over
over 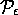 and that each
and that each 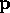 in
in 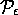 has a lattice size dividing
has a lattice size dividing 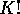 . (Note that
. (Note that 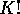 could be
replaced throughout by the least common multiple of
could be
replaced throughout by the least common multiple of 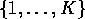 .)
If
.)
If  are
independent integer valued random variables write
are
independent integer valued random variables write 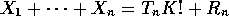 where
where  are integer valued random variables and
are integer valued random variables and 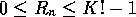 .
That is,
.
That is, 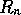 is the residue class modulo
is the residue class modulo 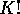 of the sum. Our
theorem is
that
of the sum. Our
theorem is
that 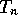 is approximately normal and that
is approximately normal and that 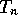 and
and 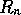 are
approximately
independent, uniformly for probabilities in
are
approximately
independent, uniformly for probabilities in 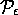 . The
distribution of
. The
distribution of 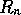 is available via an expression which may
be computed analytically for small values of
is available via an expression which may
be computed analytically for small values of 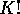 and approximately
in some other cases.
Let
and approximately
in some other cases.
Let 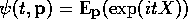 be the characteristic function of
be the characteristic function of
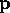 .
Let
.
Let 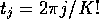 for
for 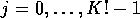 . Then
. Then

In later sections the computability of the approximation
is of less importance than the formal nature of the approximation.
We begin with the weaker form of the theorem

For a single fixed 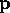 the asymptotic distribution of
the asymptotic distribution of 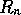 is
uniform on the set of possible residue classes and so the result
can be converted to an approximation of the conditional distribution
of
is
uniform on the set of possible residue classes and so the result
can be converted to an approximation of the conditional distribution
of 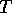 given
given  - a trivial consequence of the usual local central
limit theorem. However, under the condition that the
variates are bounded the conditional form of the result is also valid
uniformly in
- a trivial consequence of the usual local central
limit theorem. However, under the condition that the
variates are bounded the conditional form of the result is also valid
uniformly in 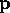 .
.
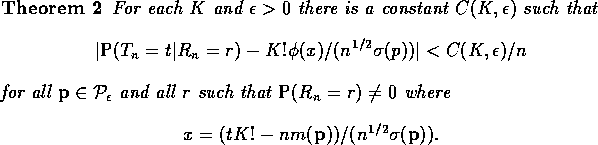
The local central limit theorem is established by analyzing the
inversion formula for the characteristic function.
We prove Theorem 1 following Petrov(??) taking
care to make error estimates uniform.
The Fourier inversion formula is

where 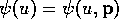 is the characteristic function of
is the characteristic function of 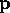 and
and
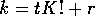 . We will split the range of integration into a number of
pieces and bound some and expand others.
Define
. We will split the range of integration into a number of
pieces and bound some and expand others.
Define 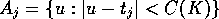 for
for 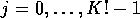 and let
and let 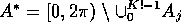 where
where
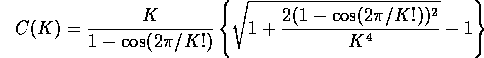

It follows from the lemma that

for every

such that
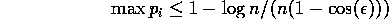
.
The integral over

will be broken into two pieces,
integrating separately over

and the complement

where

is the sequence

Over

we will expand the function

about

. Over

we will use
the following extension of Cramér's lemma.

It follows from the lemma that

In the usual proof of the local central limit theorem either the quantity

less than 1 and therefore the integral over

is exponentially small or

and the integral over

is identical to that over

where a standard Taylor expansion is used. To get a uniform result, however, we must
contemplate the

where

is slightly less than 1 so that neither
of the two cases just mentioned is applicable.

Thus for any

such that
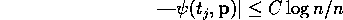
we have

Consider now a

for which
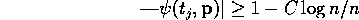
.
Define
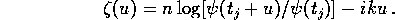
(For

the ratios in the logarithm are uniformly close to 1
permitting use of the principal branch of the logarithm throughout
the following.) We can write, for

, using a Taylor expansion
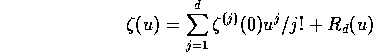
where


where
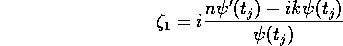
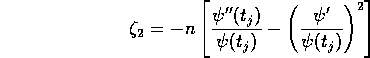

and, for all

so large that

,

Define

and
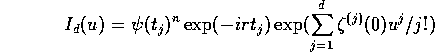
Then
since

we have
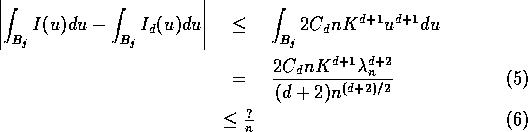
for all

larger than some integer

depending only on

and

.
On

the quantity

is bounded by

so that
On the set

we have the Taylor expansion

where
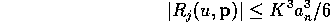
for every

.



Next: Consistency of the
Up: Maximum likelihood estimation of
Previous: The offspring distribution
Richard Lockhart
Thu Oct 26 23:26:04 PDT 1995
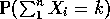 for an iid sequence
for an iid sequence  .
The approximation is proportional to the
lattice size of the underlying distribution of the
.
The approximation is proportional to the
lattice size of the underlying distribution of the  and is not a
continuous function of the underlying distribution. The probability
in question is a continuous function of this underlying
distribution and so the approximation cannot be good uniformly in the class of
possible distributions for the
and is not a
continuous function of the underlying distribution. The probability
in question is a continuous function of this underlying
distribution and so the approximation cannot be good uniformly in the class of
possible distributions for the  . Approximate likelihood methods demand
uniform approximations; in this section we provide such an approximation.
We are unable to handle the case of distributions nearly concentrated on a
single point gracefully. Moreover, it is convenient to impose the stringent
hypothesis that all distributions studied be supported on a fixed finite
set of indices
. Approximate likelihood methods demand
uniform approximations; in this section we provide such an approximation.
We are unable to handle the case of distributions nearly concentrated on a
single point gracefully. Moreover, it is convenient to impose the stringent
hypothesis that all distributions studied be supported on a fixed finite
set of indices 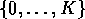 for some fixed
for some fixed 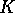 . Fix
. Fix  and let
and let 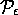 be the set of all probability distributions
be the set of all probability distributions
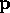 supported on the integers such that
supported on the integers such that 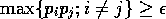 and such that
and such that  for
for 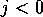 and
and 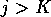 . The conditions
guarantee that the variance
. The conditions
guarantee that the variance 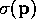 (where it seems convenient we
indicate explicitly the dependence of the mean and variance on the underlying
distribution in question) of the distribution
(where it seems convenient we
indicate explicitly the dependence of the mean and variance on the underlying
distribution in question) of the distribution 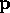 is bounded
away from
is bounded
away from  over
over 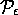 and that each
and that each 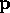 in
in 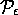 has a lattice size dividing
has a lattice size dividing 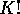 . (Note that
. (Note that 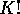 could be
replaced throughout by the least common multiple of
could be
replaced throughout by the least common multiple of 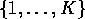 .)
If
.)
If  are
independent integer valued random variables write
are
independent integer valued random variables write 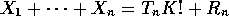 where
where  are integer valued random variables and
are integer valued random variables and 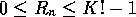 .
That is,
.
That is, 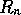 is the residue class modulo
is the residue class modulo 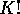 of the sum. Our
theorem is
that
of the sum. Our
theorem is
that 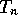 is approximately normal and that
is approximately normal and that 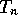 and
and 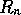 are
approximately
independent, uniformly for probabilities in
are
approximately
independent, uniformly for probabilities in 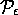 . The
distribution of
. The
distribution of 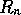 is available via an expression which may
be computed analytically for small values of
is available via an expression which may
be computed analytically for small values of 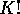 and approximately
in some other cases.
Let
and approximately
in some other cases.
Let 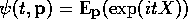 be the characteristic function of
be the characteristic function of
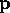 .
Let
.
Let 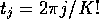 for
for 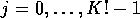 . Then
. Then


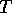 given
given  - a trivial consequence of the usual local central
limit theorem. However, under the condition that the
variates are bounded the conditional form of the result is also valid
uniformly in
- a trivial consequence of the usual local central
limit theorem. However, under the condition that the
variates are bounded the conditional form of the result is also valid
uniformly in 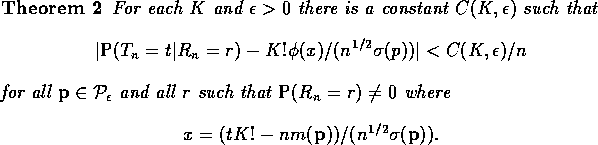

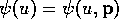 is the characteristic function of
is the characteristic function of 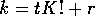 . We will split the range of integration into a number of
pieces and bound some and expand others.
Define
. We will split the range of integration into a number of
pieces and bound some and expand others.
Define 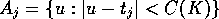 for
for 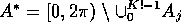 where
where