|
In this paper, we propose Continuous Graph Flow, a generative continuous flow based method that aims to model complex distributions of graph-structured data. Once learned, the model can be applied to an arbitrary graph, defining a probability density over the random variables represented by the graph. It is formulated as an
ordinary differential equation system with shared and reusable functions that operate over the graphs. This leads to a new type of neural graph message passing scheme that performs continuous message passing over time.
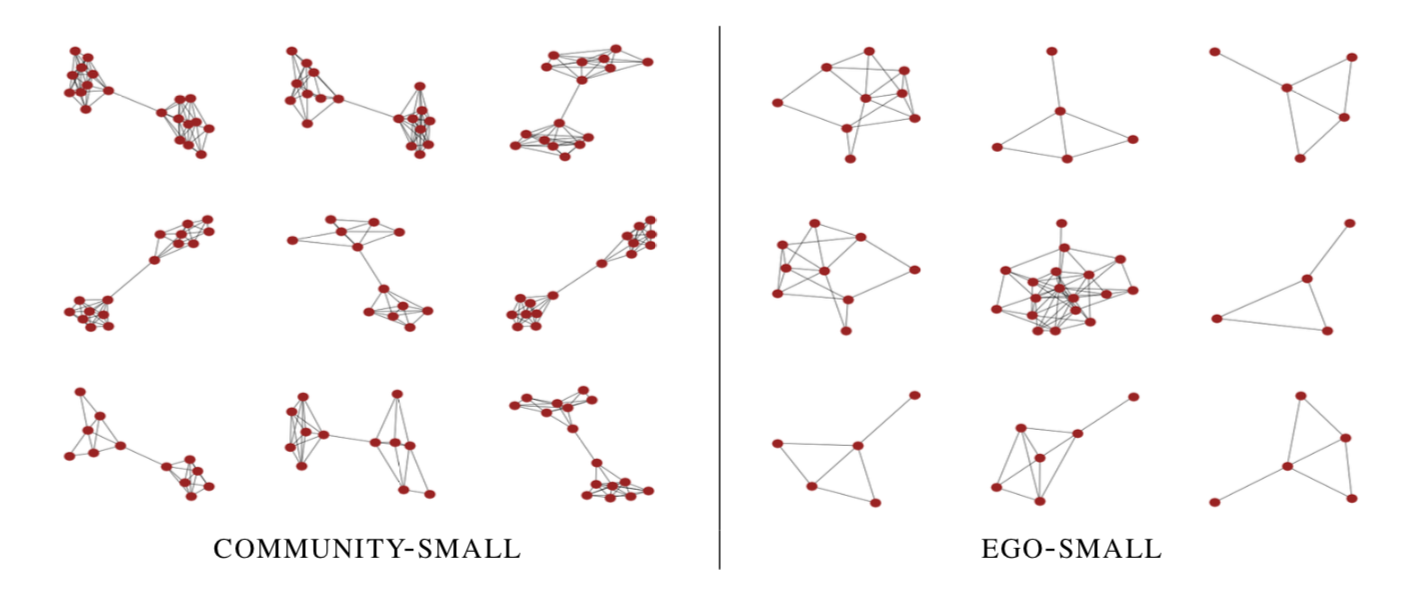
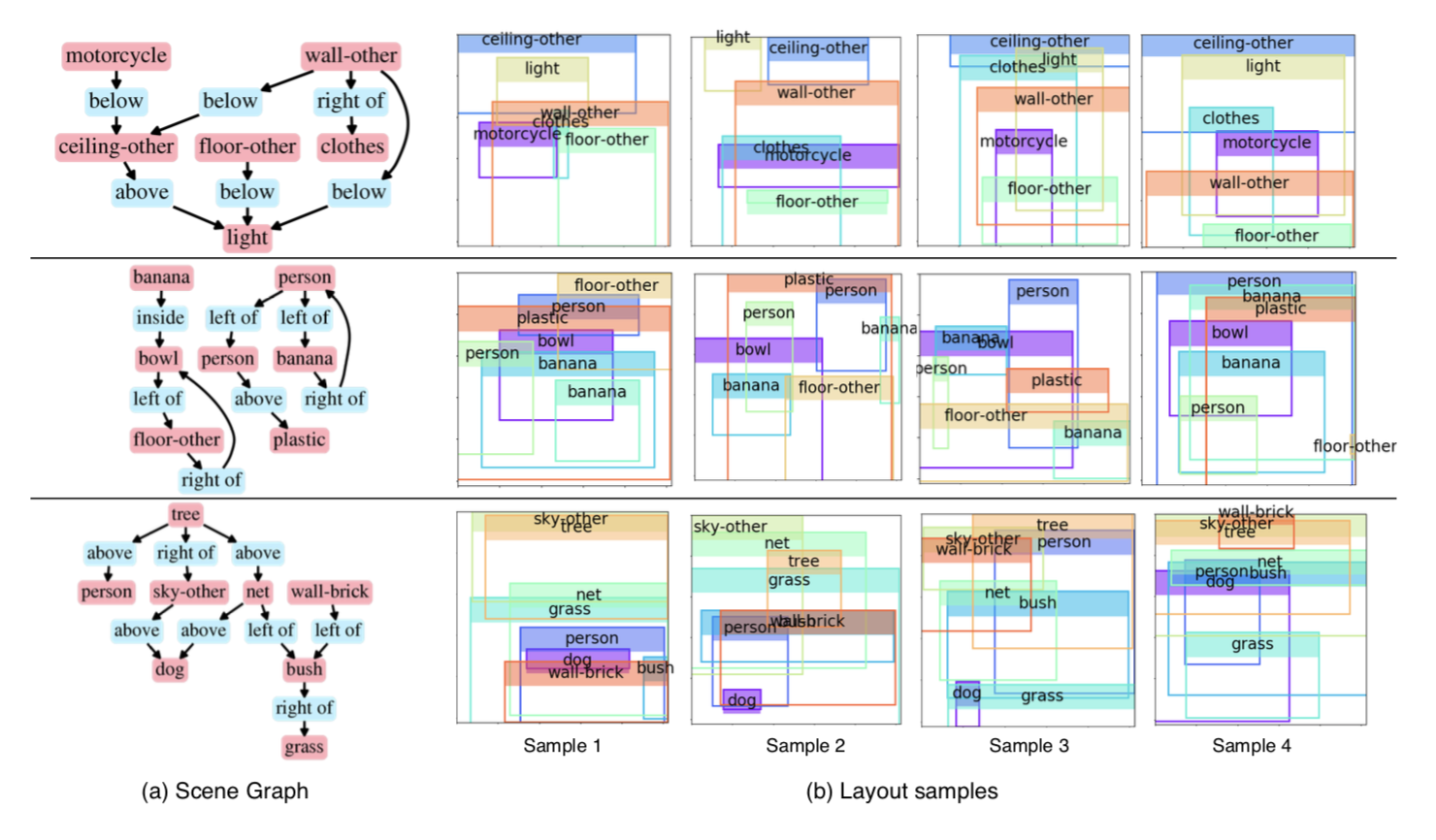
This class of models offers several advantages: a flexible representation that can generalize to variable data dimensions; ability to model dependencies in complex data distributions; reversible and memory-efficient; and exact and efficient computation of the likelihood of the data. We demonstrate the effectiveness of our model on a diverse set of generation tasks across different domains: graph generation, image puzzle generation, and layout generation from scene graphs. Our proposed model achieves significantly better performance compared to state-of-the-art models.
|