Julia Sets
This page has animated gif files illustrating the changing shapes of Julia
sets as the parameter c changes. For some examples of 'static'
Julia sets, see the
Julia page.
See also the Julia Sets Movie applet on the software page.
The gif files on this page are about 160kb each so it may take a while to download them.
Julia sets are parameterized by a complex number
c = (a,b). For some values
of c the Julia set is one piece ('connected'), while for other values
of c the Julia set is dust ('totally disconnected').
The Mandelbrot set
classifies the complex numbers into two groups; those c's where the
Julia set is connected, and those c's
where the Julia set is disconnected
(every complex number
is in exactly one of the two groups). As c varies the shape of
the Julia set varies. The animated gif files here show you several
scenarios of Julia sets as c changes.
See if you can tell when the Julia
set breaks apart inot dust (if it does).
See the
W00 course notes on Julia sets for more information.
These animated gif files were produced with MAPLE6. You may download
the program
here , or view the code (in plain text)
here .
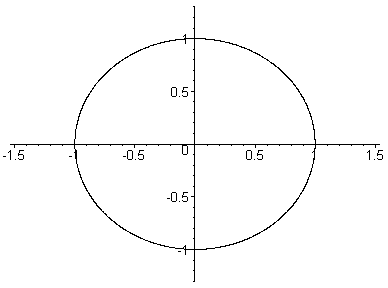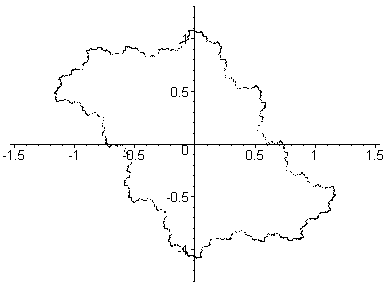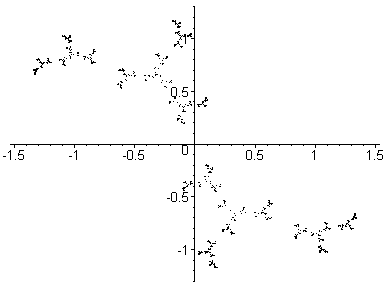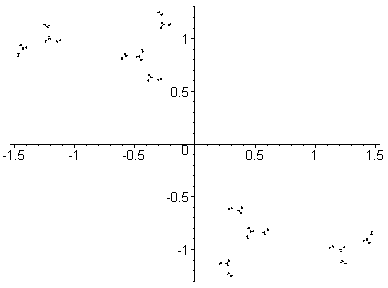 A Julia set breaking apart into dust.
Here, c goes from (0,0) to (0,1.6) in
26 steps.
This is a path up through the main body
of the
Mandelbrot set
past the Misiurewicz point (0,1).
For c=(0,0) the Julia set is a circle
(of radius 1).
For c=(0,1.6) the Julia set is dust.
At c=(0,1) the Julia set is a 'line'.
Each Julia set drawn here contains 32,768 points.
A Julia set breaking apart into dust.
Here, c goes from (0,0) to (0,1.6) in
26 steps.
This is a path up through the main body
of the
Mandelbrot set
past the Misiurewicz point (0,1).
For c=(0,0) the Julia set is a circle
(of radius 1).
For c=(0,1.6) the Julia set is dust.
At c=(0,1) the Julia set is a 'line'.
Each Julia set drawn here contains 32,768 points.
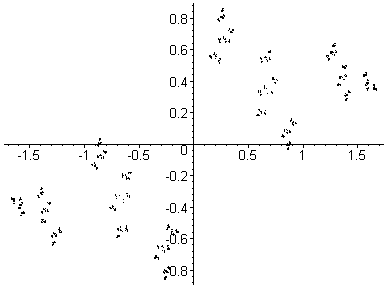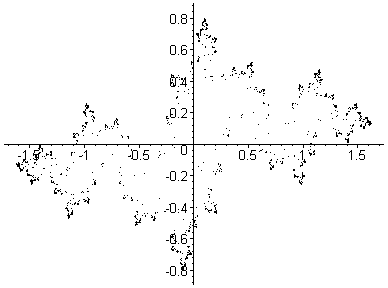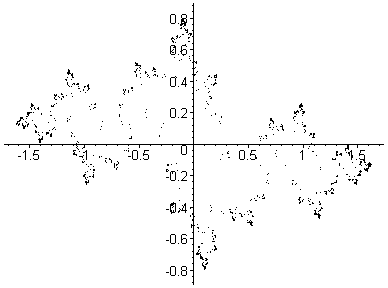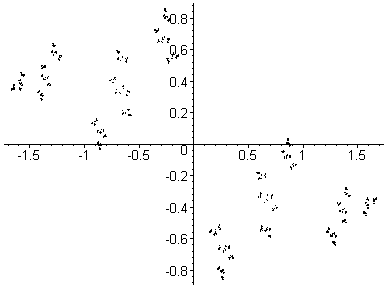 Here, c goes from (-1,-0.8) to (-1,0.8) in
26 steps. This is a path up through the 'neck'
of the Mandelbrot set.
Note that the point where
he 'head' joins the 'body'
of the Mandelbrot set
is a
parabolic point;
the associated Julia set is
just about to break apart.
Each Julia set drawn here contains 32,768 points.
Here, c goes from (-1,-0.8) to (-1,0.8) in
26 steps. This is a path up through the 'neck'
of the Mandelbrot set.
Note that the point where
he 'head' joins the 'body'
of the Mandelbrot set
is a
parabolic point;
the associated Julia set is
just about to break apart.
Each Julia set drawn here contains 32,768 points.
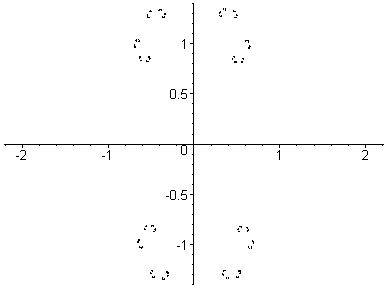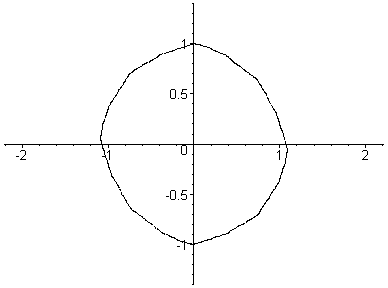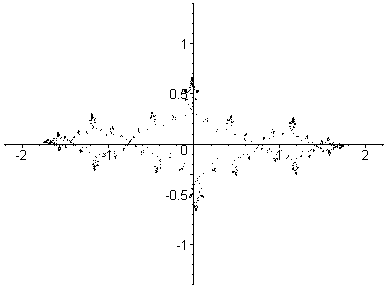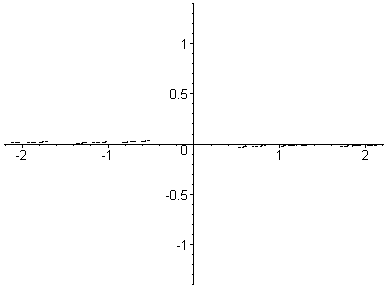 Here, c goes from (1,0.05) to (-2.4,0.05) in 29 steps.
This is a path from right to left through the centre of
the Mandelbrot set.
Each Julia set drawn here contains 2,048 points.
Here, c goes from (1,0.05) to (-2.4,0.05) in 29 steps.
This is a path from right to left through the centre of
the Mandelbrot set.
Each Julia set drawn here contains 2,048 points.
More animated Julia sets.
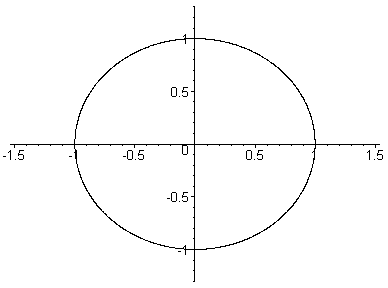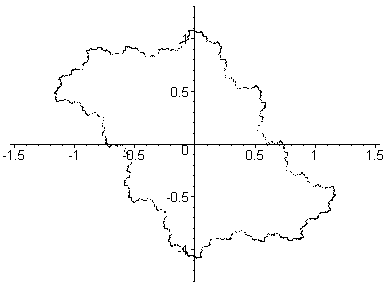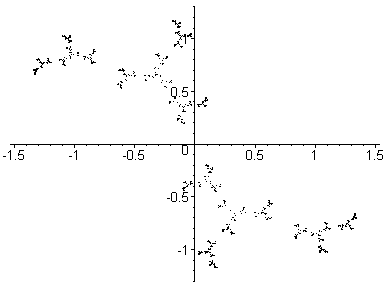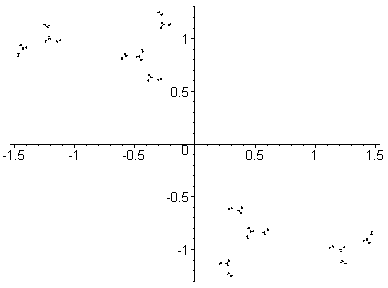 A Julia set breaking apart into dust.
Here, c goes from (0,0) to (0,1.6) in
26 steps.
This is a path up through the main body
of the
Mandelbrot set
past the Misiurewicz point (0,1).
For c=(0,0) the Julia set is a circle
(of radius 1).
For c=(0,1.6) the Julia set is dust.
At c=(0,1) the Julia set is a 'line'.
Each Julia set drawn here contains 32,768 points.
A Julia set breaking apart into dust.
Here, c goes from (0,0) to (0,1.6) in
26 steps.
This is a path up through the main body
of the
Mandelbrot set
past the Misiurewicz point (0,1).
For c=(0,0) the Julia set is a circle
(of radius 1).
For c=(0,1.6) the Julia set is dust.
At c=(0,1) the Julia set is a 'line'.
Each Julia set drawn here contains 32,768 points.
 Here, c goes from (-1,-0.8) to (-1,0.8) in
26 steps. This is a path up through the 'neck'
of the Mandelbrot set.
Note that the point where
he 'head' joins the 'body'
of the Mandelbrot set
is a
parabolic point;
the associated Julia set is
just about to break apart.
Each Julia set drawn here contains 32,768 points.
Here, c goes from (-1,-0.8) to (-1,0.8) in
26 steps. This is a path up through the 'neck'
of the Mandelbrot set.
Note that the point where
he 'head' joins the 'body'
of the Mandelbrot set
is a
parabolic point;
the associated Julia set is
just about to break apart.
Each Julia set drawn here contains 32,768 points.
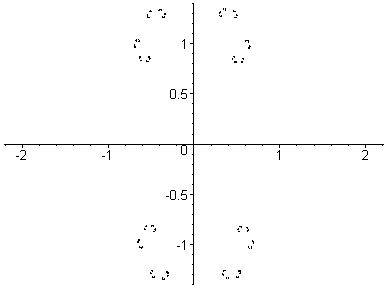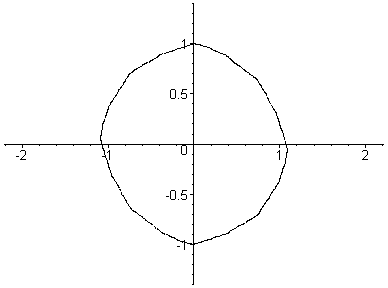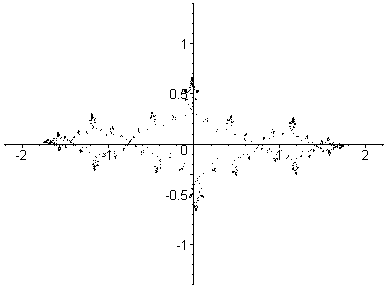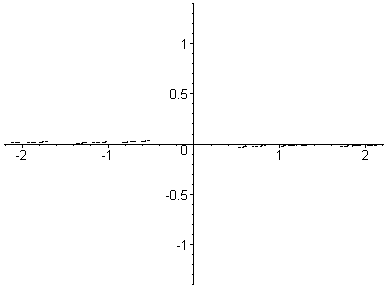 Here, c goes from (1,0.05) to (-2.4,0.05) in 29 steps.
This is a path from right to left through the centre of
the Mandelbrot set.
Each Julia set drawn here contains 2,048 points.
Here, c goes from (1,0.05) to (-2.4,0.05) in 29 steps.
This is a path from right to left through the centre of
the Mandelbrot set.
Each Julia set drawn here contains 2,048 points.