Some Julia Sets
Julia sets are defined by iterating a function (of a complex variable).
Pick a point in the complex plane (i.e., a complex number; these can
be represented as a point z=(x,y) in the plane).
Now iterate the function starting at this point. If the values of
the iterates of the function become arbitrary large (i.e., go off to
'infinity') then that point is NOT in the Julia set. If however the
point does not wander off to infinity, then that point IS in the Julia
set.
Julia sets can be simple (like a circle) or extremely complicated like a
fractal.
See the
W00 course notes on Julia sets for more information on Julia sets.
See the Julia movies page for animated images of
evolving Julia sets, and the Julia Sets Movie applet on
the software page.
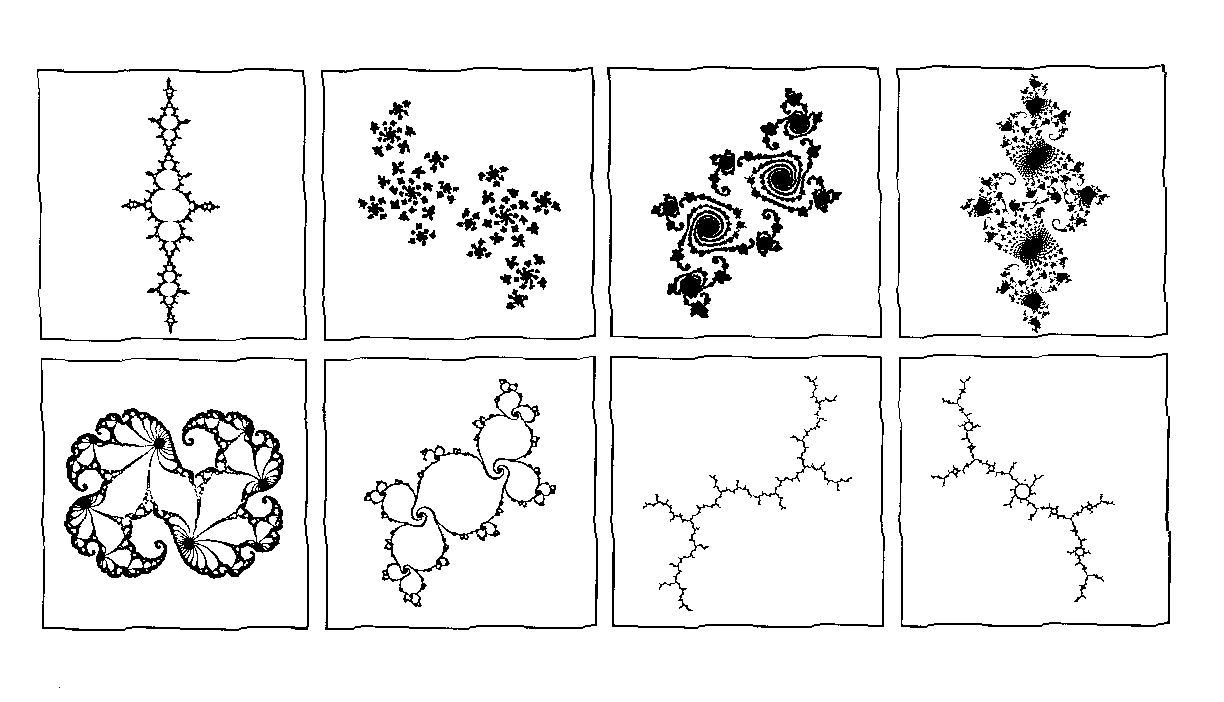
Some different types of Julia sets associated with the quadratic
map; q(z) = z^2 + c for various c.
Here, an 'IFS' algorithm was used to draw these sets.
( Larger view )
For some animations of how these Julia sets change shape as c
changes, see the
Julia movies page.
Below are some
coloured Julia sets. The colours are determined by how 'fast'
a point runs off to infinity under iteration by the associated
function. The algorithm
used to draw these Julia sets is different from the algorithm used to
draw the Julia sets above (the algorithm
used to draw the coloured Julia sets is much more computationally
intensive than the 'IFS' algorithm).
A selection of 4 Julia sets associated with the quadratic map.
(Larger view)
The patchiness is an artifact of the scanning (i.e., it is not a feature of the
Julia set).
Juila set associated with the exponential function; 2*pi*i exp(z).
As above, the patchiness is an artifact of the scanning process.
(Larger view)
Julia set associated with the sine function; (1+0.2i)*sin(z).
( Larger view)
Julia set associated with the cosine function; 2.95*cos(z).
(Larger view)