My general field of research is in dynamical systems, and the
following is a brief overview of some major themes; the main emphasis
is on analytical and numerical studies of partial differential
equations exhibiting spatiotemporally complex and chaotic dynamics,
but applications to other fields have also captured my attention...
I welcome inquiries from potential students interested in these or
related topics.
Pattern Formation and Spatiotemporal Chaos:
Numerous partial differential equations (PDEs) arising in contexts
such as fluid dynamics or surface growth display surprisingly complex
temporal dynamics and/or spatial pattern formation. The
Kuramoto-Sivashinsky
(KS) equation is a particularly rich (and much-studied) example,
and I have long been interested in investigating various aspects of
spatiotemporal chaos in the KS equation and its generalizations,
analytically and numerically.
In recent years I have focussed especially on a related 6th-order PDE,
the Nikolaevskiy model for short-wave pattern formation with Galilean
invariance, and its associated Matthews-Cox modulation
equations. Work with my former student Philip Poon revealed
spatiotemporal chaos with strong scale separation, potential anomalous
scaling, Burgers-like viscous shocks and coarsening phenomena to
chaos-stabilized fronts; there is much that remains to be done to
understand this curious dynamical behaviour!
Applied Analysis:
While the solutions of such nonlinear PDEs are typically too complex
to permit detailed analytical description, rigorous
functional-analytic estimates on global, long-time or averaged
properties of solutions on the attractor may nevertheless often be
proved.
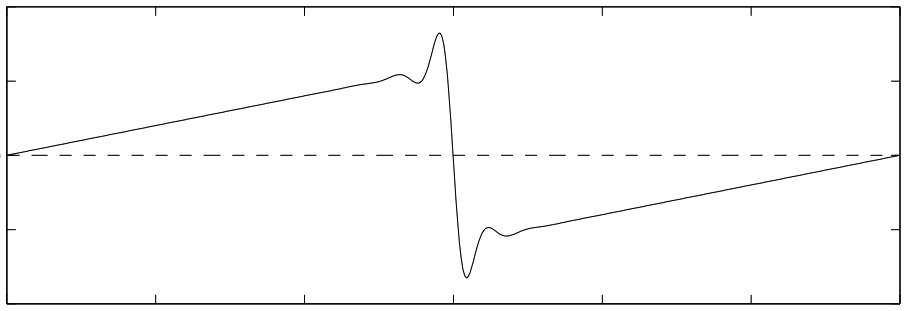
I
am especially interested in the interplay between numerical and
analytical results; as an example, my numerical discovery and
asymptotic investigation of a viscous shock solution in the
destabilized KS equation influenced subsequent improvements in, and
constraints on, rigorous bounds on the scaling of the absorbing ball
for the KS equation.
A related major theme of my research concerns analytical estimates in
fluid dynamics, notably turbulent Rayleigh-Bénard convection, for
which I am particularly interested in establishing rigorous
a
priori variational bounds on averaged quantities such as bulk
convective heat transport.
Modelling:
I have collaborated on and (co-)supervised students interested in
dynamical models in various areas, including mathematical epidemiology
and immunology, aggregation models and opinion dynamics. For
much of this research, I am associated with the
IMPACT-HIV
group (based at the
IRMACS Centre
at SFU), an interdisciplinary research team studying differential
equation and network models of the HIV epidemic, with a particular
focus on evaluating Treatment as Prevention control strategies.
