Empirical Bayes Estimation compared to Original SMR scores

Original SMR Ranking and Error Ranking of the LHA units

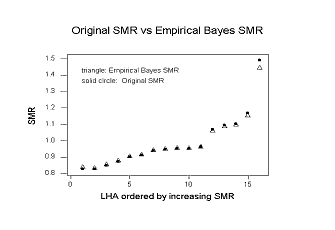
After applying a paired T test on both the original SMR scores and those generated by the empirical Bayes estimation no significant difference between the two sets of the data could be determined. Consequently, the original SMR scores were then used to compare with the SES factors of the five deprivation indices. The reason for little noticeable difference could be related to the large number of LHA units with little variation between their expected and observed counts of mortality. The estimated parameters a and n are very similar. This is implicative of a low influence between the parameters and the expected and observed mortality counts. The map depicting SMR scores (Map Appendix) draws a comparison to the relatively high risk (SMR > 1) and low risk (SMR < 1) LHAs. The variance (Map Appendix) displays the standard error within each LHA, drawing a comparison from the estimations. In most instances there was a positive correlation between areas with large standard error (or variance) and high SMR scores. However, West Vancouver, which has the smallest SMR value, has a relatively large standard error compared with the areas that have similar deprived values. Reasons for this were perhaps associated with the relatively small population size of the area.    

95% CI for mean difference: (-0.00477, 0.01020)

T-Test of mean difference = 0 (vs not = 0): T-Value = 0.77  P-Value = 0.452

The correlation coefficients were calculated and listed below.  The correlation coefficient is a measure of degree of linear relationship between two variables.

 The mean of the original SMR was 0.9912.  The differences between the original SMR and Bayes estimation are only greater within the LHA units whose original SMR is greater than 1.  The highest original SMR was associated with the Downtown Eastside, with an original SMR score of 1.49405. This number was calculated at 1.44412 after running the Bayes estimation. Although the difference between the two scores was 0.04993, it was the largest among the LHA units.

 All correlations between each index and SMR show moderate linear relationships.  The DETR Index of Multiple Deprivation had the strongest correlation out of the five indices. The correlation between the most deprived LHA (by SMR score) with the location of the most deprived LHA (the Downtown Eastside) identified by the deprivation index coincides within the DETR, SDD and TOWNSEND indices. Interestingly, the Jarman and SCOTDEP indices ranked City Center the highest. The variations between the deprivation indices grew stronger as the comparisons looked at LHA units further from the extreme. There was little correlation within the LHA units with low SMR scores and the deprivation indices. One possible explanation of this account is the high degree of variability within the deprivation scores. The wide range of factors and weightings could account for these discrepancies. Ultimately, the strongest correlation between predicting SES ranking with levels of mortality was only consistent in units with an SMR value greater than 1. This is noteworthy, as the purpose of a deprivation index is to depict areas of inequality and health. Question remains as to whether these same indices can determine to the same affect levels associated near SMR counts near the midrange units.