Profile Likelihood Confidence Intervals

The MODEL Procedure

Profile Likelihood Confidence Intervals

Wald-based and likelihood ratio-based confidence intervals are available in the MODEL procedure for computing a confidence interval on an estimated parameter. A confidence interval on a parameter ${\theta}$ can be constructed by inverting a Wald-based or a likelihood ratio-based test.

The approximate ${100(1-{\alpha})}$ % Wald confidence interval for a parameter ${\theta}$ is

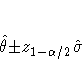
$\hat{{\theta}} {+-} z_{1-{\alpha}/2}\hat{{\sigma}}$

where z_p is the 100pth percentile of the standard normal distribution, ${\hat{{\theta}}}$ is the maximum likelihood estimate of ${\theta}$ , and ${\hat{{\sigma}}}$ is the standard error estimate of ${\hat{{\theta}}}$ .

A likelihood ratio-based confidence interval is derived from the ${{\chi}^2}$ distribution of the generalized likelihood ratio test. The approximate ${1-{\alpha}}$ confidence interval for a parameter ${\theta}$ is

${\theta} : 2[{\ssbeleven l(\hat{{\theta}}) - l({\theta})}] {\leq} q_{1,1-{\alpha}} = 2 l^{{\ast}}$

where ${q_{1,1-{\alpha}}}$ is the ${(1-{\alpha})}$ quantile of the ${{\chi}^2}$ with one degree of freedom, and ${l({\theta})}$ is the log likelihood as a function of one parameter. The endpoints of a confidence interval are the zeros of the function ${l({\theta}) - l^{{\ast}}}$ .Computing a likelihood ratio-based confidence interval is an iterative process. This process must be performed twice for each parameter, so the computational cost is considerable. Using a modified form of the algorithm recommended by Venzon and Moolgavkar (1988), you can determine that the cost of each endpoint computation is approximately the cost of estimating the original system.

To request confidence intervals on estimated parameters, specify the following option in the FIT statement:

PRL= WALD | LR | BOTH

By default the PRL option produces 95% likelihood ratio confidence limits. The coverage of the confidence interval is controlled by the ALPHA= option in the FIT statement.

The following is an example of the use of the confidence interval options:

      data exp;
         do time = 1 to 20;
            y = 35 * exp( 0.01 * time ) + 5*rannor( 123 );
         output;
         end;
      run;
   
      proc model data=exp;    
         parm zo 35 b;
            dert.z = b * z;
            y=z;
         fit y init=(z=zo) / prl=both;
         test zo = 40.475437 ,/lr;
      run;

The output from the requested confidence intervals and the TEST statement are shown in Figure 14.47

The MODEL Procedure

Nonlinear OLS Parameter Estimates
Parameter	Estimate	Approx Std Err	t Value	Approx Pr > \|t\|
zo	36.58933	1.9471	18.79	<.0001
b	0.006497	0.00464	1.40	0.1780

Test Results
Test	Type	Statistic	Pr > ChiSq	Label
Test0	L.R.	3.81	0.0509	zo = 40.475437

Parameter Wald 95% Confidence Intervals
Parameter	Value	Lower	Upper
zo	36.5893	32.7730	40.4056
b	0.00650	-0.00259	0.0156

Parameter Likelihood Ratio 95% Confidence Intervals
Parameter	Value	Lower	Upper
zo	36.5893	32.8381	40.4921
b	0.00650	-0.00264	0.0157

Figure 14.47: Confidence Interval Estimation

Note that the likelihood ratio test reported the probability that zo = 40.47543 is 5% but zo = 40.47543 is the upper bound of a 95% confidence interval. To understand this conundrum, note that the TEST statement is using the likelihood ratio statistic to test the null hypothesis H₀ : zo = 40.47543 with the alternate that ${H_{a} : zo {\neq} 40.47543}$ . The upper confidence interval can be viewed as a test with the null hypothesis H₀ : zo < = 40.47543.

Chapter Contents
Previous
Next
Top