Parameter Estimation

The STATESPACE Procedure

Parameter Estimation

The model is z_t+1 = Fz_t+Ge_t+1, where e_t is a sequence of independent multivariate normal innovations with mean vector 0 and variance ${{\Sigma}_{ee}}$ .The observed sequence, x_t, composes the first r components of z_t and, thus, x_t = Hz_t, where H is the r ×s matrix [I_r 0].

Let E be the r ×n matrix of innovations:

$E = [\matrix{e_{1} & { ... } & e_{n} }]$

If the number of observations, n, is reasonably large, the log likelihood, L, can be approximated up to an additive constant as follows:

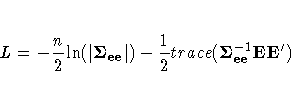
$L = -\frac{n}2 {\ln}( {|{\Sigma}_{ee}|} ) -\frac{1}2 {trace}( {\Sigma}^{-1}_{ee} {EE}')$

The elements of ${{\Sigma}_{ee}}$ are taken as free parameters and are estimated as follows:

S₀ = [1/n]EE'

Replacing ${{\Sigma}_{ee}}$ by S₀ in the likelihood equation, the log likelihood, up to an additive constant, is

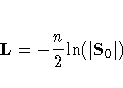
$L = -\frac{n}2{\ln}( {|{S}_{0}|} )$

Letting B be the backshift operator, the formal relation between x_t and e_t is

x_t = H(I-BF)^-1Ge_t

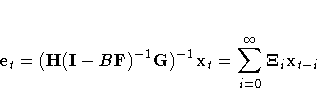
$e_{t} = (H(I-B{F})^{-1}G)^{-1}x_{t} = \sum_{i=0}^{{\infty}}{{\Xi}_{i}x_{t-i} }$

Letting C_i be the ith lagged sample covariance of x_t, and neglecting end effects, the matrix S₀ is

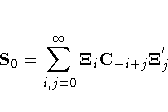
$S_{0} = \sum_{i,j=0}^{{\infty}}{{\Xi}_{i}C_{-i+j} {\Xi}^{'}_{j} }$

For the computation of S₀, the infinite sum is truncated at the value of the KLAG= option. The value of the KLAG= option should be large enough that the sequence ${{\Xi}_{i}}$ is approximately 0 beyond that point.

Let ${{\theta}}$ be the vector of free parameters in the F and G matrices. The derivative of the log likelihood with respect to the parameter ${{\theta}}$ is

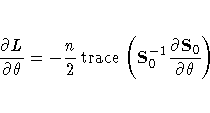
$\frac{{\partial}L}{{\partial}{\theta}} = -\frac{n}2 \,{\rm trace}( S^{-1}_{0} \frac{{\partial}S_{0}}{{\partial}{\theta}} )$

The second derivative is

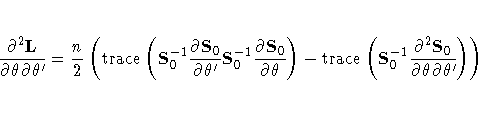
$\frac{{\partial}^2{L}}{{\partial}{\theta}{\partial}{\theta}'} = \frac{n}2( {\rm... ...-1}_{0} \frac{{\partial}^2{S}_{0}}{{\partial}{\theta}{\partial}{\theta}'} ) )$

Near the maximum, the first term is unimportant and the second term can be approximated to give the following second derivative approximation:

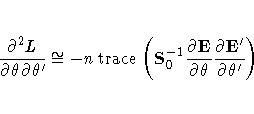
$\frac{{\partial}^2L}{{\partial}{\theta}{\partial}{\theta}'} \cong -n\, {\rm tra... ...ac{{\partial}E}{{\partial}{\theta}} \frac{{\partial}E'}{{\partial}{\theta}' })$

The first derivative matrix and this second derivative matrix approximation are computed from the sample covariance matrix C₀ and the truncated sequence ${{\Xi}_{i}}$ .The approximate likelihood function is maximized by a modified Newton-Raphson algorithm employing these derivative matrices.

The matrix S₀ is used as the estimate of the innovation covariance matrix, ${{\Sigma}_{ee}}$ .The negative of the inverse of the second derivative matrix at the maximum is used as an approximate covariance matrix for the parameter estimates. The standard errors of the parameter estimates printed in the parameter estimates tables are taken from the diagonal of this covariance matrix. The parameter covariance matrix is printed when the COVB option is specified.

If the data are nearly nonstationary, a better estimate of ${{\Sigma}_{ee}}$ and the other parameters can sometimes be obtained by specifying the RESIDEST option. The RESIDEST option estimates the parameters using conditional least squares instead of maximum likelihood.

The residuals are computed using the state space equation and the sample mean values of the variables in the model as start-up values. The estimate of S₀ is then computed using the residuals from the ith observation on, where i is the maximum number of times any variable occurs in the state vector. A multivariate Gauss-Marquardt algorithm is used to minimize ${{|{S}_{0}|}}$ .Refer to Harvey (1981a) for a further description of this method.

Chapter Contents
Previous
Next
Top