Canonical Correlation Analysis

Chapter Contents

The STATESPACE Procedure

Canonical Correlation Analysis

Given the order p, let p_t be the vector of current and past values relevant to prediction of x_t+1:

p_t = ( x'_t, x'_t-1, ... , x'_t-p)'

Let f_t be the vector of current and future values:

f_t = ( x'_t, x'_t+1, ... , x'_t+p)'

In the canonical correlation analysis, consider submatrices of the sample covariance matrix of p_t and f_t. This covariance matrix, V, has a block Hankel form:

$V=[\matrix{ C_{0} & C'_{1} & C'_{2} & { ... } & C'_{p} \cr C'_{1} & C'_{2} & C... ...ace*{1pt} & {\vdots} \cr C'_{p} & C'_{p+1} & C'_{p+2} & { ... } & C'_{2p} } ]$

State Vector Selection Process

The canonical correlation analysis forms a sequence of potential state vectors, z^j_t. Examine a sequence, f^j_t, of subvectors of f_t, and form the submatrix, V^j, consisting of the rows and columns of V corresponding to the components of f^j_t, and compute its canonical correlations.

The smallest canonical correlation of V^j is then used in the selection of the components of the state vector. The selection process is described in the following. For more details about this process, refer to Akaike (1976).

In the following discussion, the notation ${x_{t+k| t}}$ denotes the wide sense conditional expectation (best linear predictor) of x_t+k, given all x_s with s less than or equal to t. In the notation x_i,t+1, the first subscript denotes the ith component of x_t+1.

The initial state vector z¹_t is set to x_t. The sequence f^j_t is initialized by setting

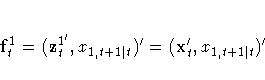
$f^1_{t} = ( z^{1'}_{t}, x_{1,t+1| t})' = ( x'_{t}, x_{1,t+1| t})'$

That is, start by considering whether to add x_1,t+1|t to the initial state vector z¹_t.

The procedure forms the submatrix V¹ corresponding to f¹_t and computes its canonical correlations. Denote the smallest canonical correlation of V¹ as ${{\rho}_{min}}$ .If ${{\rho}_{min}}$ is significantly greater than 0, x_1,t+1|t is added to the state vector.

If the smallest canonical correlation of V¹ is not significantly greater than 0, then a linear combination of f¹_t is uncorrelated with the past, p_t. Assuming that the determinant of C₀ is not 0, (that is, no input series is a constant), you can take the coefficient of x_1,t+1|t in this linear combination to be 1. Denote the coefficients of z¹_t in this linear combination as l. This gives the relationship:

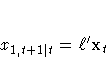
$x_{1,t+1| t} = {{\ell}}'x_{t}$

Therefore, the current state vector already contains all the past information useful for predicting x_1,t+1 and any greater leads of x_1,t. The variable x_1,t+1|t is not added to the state vector, nor are any terms x_1,t+k|t considered as possible components of the state vector. The variable x₁ is no longer active for state vector selection.

The process described for x_1,t+1|t is repeated for the remaining elements of f_t. The next candidate for inclusion in the state vector is the next component of f_t corresponding to an active variable. Components of f_t corresponding to inactive variables that produced a zero ${{\rho}_{min}}$ in a previous step are skipped.

Denote the next candidate as x_l,t+k|t. The vector f^j_t is formed from the current state vector and x_l,t+k|t as follows:

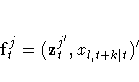
${ f^j_{t}} = ( z^{j'}_{t}, x_{l,t+k| t} )'$

The matrix V^j is formed from f^j_t and its canonical correlations are computed. The smallest canonical correlation of V^j is judged to be either greater than or equal to 0. If it is judged to be greater than 0, x_l,t+k|t is added to the state vector. If it is judged to be 0, then a linear combination of f^j_t is uncorrelated with the p_t, and the variable x_l is now inactive.

The state vector selection process continues until no active variables remain.

Testing Significance of Canonical Correlations

For each step in the canonical correlation sequence, the significance of the smallest canonical correlation, ${{\rho}_{min}}$ , is judged by an information criterion from Akaike (1976). This information criterion is

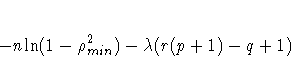
$-n {\ln}( 1- {\rho}^2_{min} )-{\lambda}( r (p+1)-q+1 )$

where q is the dimension of f^j_t at the current step, r is the order of the state vector, p is the order of the vector autoregressive process, and ${\lambda}$ is the value of the SIGCORR= option. The default is SIGCORR=2. If this information criterion is less than or equal to 0, ${{\rho}_{min}}$ is taken to be 0; otherwise, it is taken to be significantly greater than 0. (Do not confuse this information criterion with the AIC.)

Variables in ${x_{t+p| t}}$ are not added in the model, even with positive information criterion, because of the singularity of V. You can force the consideration of more candidate state variables by increasing the size of the V matrix by specifying a PASTMIN= option value larger than p.

Printing the Canonical Correlations

To print the details of the canonical correlation analysis process, specify the CANCORR option in the PROC STATESPACE statement. The CANCORR option prints the candidate state vectors, the canonical correlations, and the information criteria for testing the significance of the smallest canonical correlation.

Bartlett's ${{\chi}^2}$ and its degrees of freedom are also printed when the CANCORR option is specified. The formula used for Bartlett's ${{\chi}^2}$ is

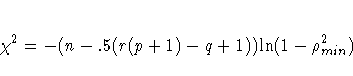
${\chi}^2 = - ( n-.5 ( r (p+1)-q+1 ) ) {\ln}( 1- {\rho}^2_{min} )$

with r (p+1)-q+1 degrees of freedom.

Figure 18.11 shows the output of the CANCORR option for the introductory example shown in the "Getting Started" section of this chapter.

The STATESPACE Procedure

Canonical Correlations Analysis

x(T;T)	y(T;T)	x(T+1;T)	Information Criterion	Chi Square	DF
1	1	0.237045	3.566167	11.4505	4

x(T;T)	y(T;T)	x(T+1;T)	y(T+1;T)	Information Criterion	Chi Square	DF
1	1	0.238244	0.056565	-5.35906	0.636134	3

x(T;T)	y(T;T)	x(T+1;T)	x(T+2;T)	Information Criterion	Chi Square	DF
1	1	0.237602	0.087493	-4.46312	1.525353	3

Figure 18.11: Canonical Correlations Analysis

New variables are added to the state vector if the information criteria are positive. In this example, $y_{t+1| t}$ and $x_{t+2| t}$ are not added to the state space vector because the information criteria for these models are negative.

If the information criterion is nearly 0, then you may want to investigate models that arise if the opposite decision is made regarding ${{\rho}_{min}}$ .This investigation can be accomplished by using a FORM statement to specify part or all of the state vector.

Preliminary Estimates of F

When a candidate variable x_l,t+k|t yields a zero ${{\rho}_{min}}$ and is not added to the state vector, a linear combination of f^j_t is uncorrelated with the p_t. Because of the method used to construct the f^j_t sequence, the coefficient of x_l,t+k|t in l can be taken as 1. Denote the coefficients of z^j_t in this linear combination as l.

This gives the relationship:

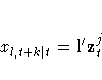
$x_{l,t+k| t} = l' z^j_{t}$

The vector l is used as a preliminary estimate of the first r columns of the row of the transition matrix F corresponding to x_l,t+k-1|t.

Chapter Contents
Previous
Next
Top