The Two-Way Random Effects Model

The TSCSREG Procedure

The Two-Way Random Effects Model

The specification for the two way model is

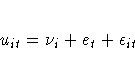
$u_{it}={\nu}_{i}+e_{t} + {\epsilon}_{it}$

For balanced data, the two-way random effects model is estimated using the method of Fuller and Battese (1974), so in this case, the RANTWO option is equivalent to the FULLER option already existing in PROC TSCSREG.

The following method (Wansbeek and Kapteyn 1989) is used to handle unbalanced data.

Let X_* and ${y_{{\ast}}}$ be the independent and dependent variables arranged by time and by cross section within each time period. Let M_t be the number of cross sections observed in time t and ${\sum_{t}M_{t}=M}$ . Let D_t be the M_t× N matrix obtained from the N × N identity matrix from which rows corresponding to cross sections not observed at time t have been omitted. Consider

Z = (Z₁, Z₂)

where Z₁ = ( D'₁, D'₂, ... .. D'_T)'and Z₂ = diag(D₁j_N,D₂j_N, ... ... D_Tj_N).

The matrix Z gives the dummy variable structure for the two-way model.

Let

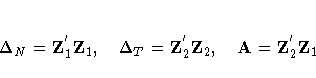
${\Delta}_{N}= Z^{'}_{1}Z_{1},\hspace*{1em} {\Delta}_{T}= Z^{'}_{2}Z_{2},\hspace*{1em} A= Z^{'}_{2}Z_{1}$

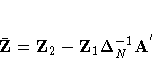
${\bar{Z}}=Z_{2}-Z_{1} {\Delta}^{-1}_{N}A^{'}$

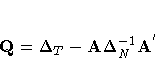
$Q={\Delta}_{T}-A {\Delta}^{-1}_{N} A^{'}$

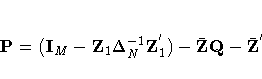
$P=(I_{M} - Z_{1} {\Delta}^{-1}_{N} Z^{'}_{1}) - {\bar{Z}}Q - {\bar{Z}}^{'}$

The estimator of the error variance is

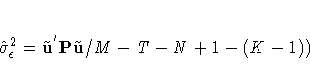
$\hat{{\sigma}}^2_{{\epsilon}}= \tilde{u}^{'}P\tilde{u}/M-T-N+1-(K-1))$

where the ${\tilde{u}}$ are given by $\tilde{u}=(I_{M}-j_{M} j{'}_{M}/M) (y_{\ast}-X_{{\ast} s} ( X{'}_{{\ast} s} {PX}_{{\ast} s})^{-1} X_{{\ast} s}{'}P{y}_{\ast})$ if there is an intercept and by ${\tilde{u}=(y_{{\ast}}-X_{{\ast} s} ( X{'}_{{\ast} s} {PX}_{{\ast} s})^{-1} X{'}_{{\ast} s}{Py}_{{\ast}} }$ if there is not.

The estimation of the variance components is performed by using a quadratic unbiased estimation (QUE) method that involves focusing on quadratic forms of the residuals ${\tilde{u}}$ , equating their expected values to the realized quadratic forms, and solving for the variance components.

Let

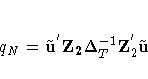
$q_{N}=\tilde{u}^{'} {Z_{2}} {\Delta}^{-1}_{T} Z_{2}^{'}\tilde{u}$

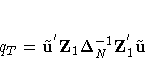
$q_{T}=\tilde{u}^{'}Z_{1} {\Delta}^{-1}_{N}Z_{1}^{'}\tilde{u}$

Consider the expected values

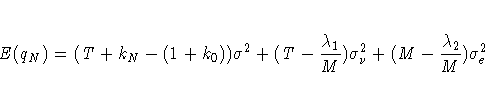
$E(q_{N})=(T+k_{N} - (1+k_{0})){\sigma}^2 + (T - \frac{{\lambda}_{1}}{M}) {\sigma}^2_{{\nu}} + (M - \frac{{\lambda}_{2}}{M}) {\sigma}^2_{e}$

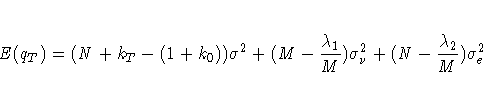
$E(q_{T})=(N+k_{T} - (1+k_{0})){\sigma}^2 + ( M - \frac{{\lambda}_{1}}{M}) {\sigma}^2_{{\nu}} + (N - \frac{{\lambda}_{2}}{M}) {\sigma}^2_{e}$

where

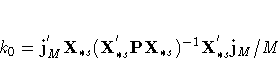
$k_{0}= j^{'}_{M} X_{{\ast} s}( X^{'}_{{\ast} s} {PX}_{{\ast} s})^{-1} X^{'}_{{\ast} s} j_{M} / M$

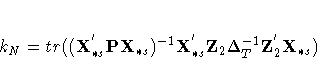
$k_{N}= tr( ( X^{'}_{{\ast} s} {PX}_{{\ast} s})^{-1} X^{'}_{{\ast} s} Z_{2} {\Delta}^{-1}_{T} Z_{2}^{'}X_{{\ast} s} )$

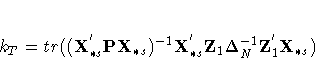
$k_{T}= tr( ( X^{'}_{{\ast} s} {PX}_{{\ast} s})^{-1} X^{'}_{{\ast} s} Z_{1} {\Delta}^{-1}_{N}Z_{1}^{'} X_{{\ast} s} )$

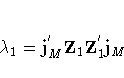
${\lambda}_{1} = j^{'}_{M} Z_{1} Z^{'}_{1} j_{M}$

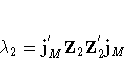
${\lambda}_{2}= j^{'}_{M} Z_{2} Z^{'}_{2} j_{M}$

The quadratic unbiased estimators for ${ {\sigma}^2_{{\nu}} }$ and ${ {\sigma}^2_{e}}$ are obtained by equating the expected values to the quadratic forms and solving for the two unknowns.

The estimated generalized least squares procedure substitute the QUE estimates into the covariance matrix of the composite error term u_it, which is given by

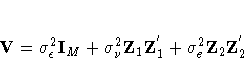
$V= {\sigma}^2_{{\epsilon}}I_{M} + {\sigma}^2_{{\nu}}Z_{1} Z^{'}_{1} + {\sigma}^2_{e}Z_{2} Z^{'}_{2}$

Chapter Contents
Previous
Next
Top