Example 7.1: Simulated IMA Model

The ARIMA Procedure

Example 7.1: Simulated IMA Model

This example illustrates the ARIMA procedure results for a case where the true model is known. An integrated moving average model is used for this illustration.

The following DATA step generates a pseudo-random sample of 100 periods from the ARIMA(0,1,1) process u_t = u_t-1 + a_t - .8a_t-1, a_t iid N(0,1).


   title1 'Simulated IMA(1,1) Series';
   data a;
     u1 = 0.9; a1 = 0;
     do i = -50 to 100;
        a = rannor( 32565 );
        u = u1 + a - .8 * a1;
        if i > 0 then output;
        a1 = a;
        u1 = u;
        end;
   run;

The following ARIMA procedure statements identify and estimate the model.


   proc arima data=a;
     identify var=u nlag=15;
     run;
     identify var=u(1) nlag=15;
     run;
     estimate q=1 ;
     run;
   quit;

The results of the first IDENTIFY statement are shown in Output 7.1.1. The output shows the behavior of the sample autocorrelation function when the process is nonstationary. Note that in this case the estimated autocorrelations are not very high, even at small lags. Nonstationarity is reflected in a pattern of significant autocorrelations that do not decline quickly with increasing lag, not in the size of the autocorrelations.

Output 7.1.1: Output from the First IDENTIFY Statement

Simulated IMA(1,1) Series

The ARIMA Procedure

Name of Variable = u
Mean of Working Series	0.099637
Standard Deviation	1.115604
Number of Observations	100

Autocorrelations
Lag	Covariance	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1	Std Error
0	1.244572	1.00000	\| \|********************\|	0
1	0.547457	0.43988	\| . \|********* \|	0.100000
2	0.534787	0.42970	\| . \|********* \|	0.117770
3	0.569849	0.45787	\| . \|********* \|	0.132524
4	0.384428	0.30888	\| . \|****** \|	0.147497
5	0.405137	0.32552	\| . \|******* \|	0.153830
6	0.253617	0.20378	\| . \|**** . \|	0.160571
7	0.321830	0.25859	\| . \|***** . \|	0.163136
8	0.363871	0.29237	\| . \|******. \|	0.167185
9	0.271180	0.21789	\| . \|**** . \|	0.172222
10	0.419208	0.33683	\| . \|******* \|	0.174957
11	0.298127	0.23954	\| . \|***** . \|	0.181326
12	0.186460	0.14982	\| . \|*** . \|	0.184463
13	0.313270	0.25171	\| . \|***** . \|	0.185676
14	0.314594	0.25277	\| . \|***** . \|	0.189057
15	0.156329	0.12561	\| . \|*** . \|	0.192407

"." marks two standard errors

The ARIMA Procedure

Inverse Autocorrelations
Lag	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
1	-0.12382	\| . **\| . \|
2	-0.17396	\| .***\| . \|
3	-0.19966	\| ****\| . \|
4	-0.01476	\| . \| . \|
5	-0.02895	\| . *\| . \|
6	0.20612	\| . \|**** \|
7	0.01258	\| . \| . \|
8	-0.09616	\| . **\| . \|
9	0.00025	\| . \| . \|
10	-0.16879	\| .***\| . \|
11	0.05680	\| . \|* . \|
12	0.14306	\| . \|***. \|
13	-0.02466	\| . \| . \|
14	-0.15549	\| .***\| . \|
15	0.08247	\| . \|** . \|

Partial Autocorrelations
Lag	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
1	0.43988	\| . \|********* \|
2	0.29287	\| . \|****** \|
3	0.26499	\| . \|***** \|
4	-0.00728	\| . \| . \|
5	0.06473	\| . \|* . \|
6	-0.09926	\| . **\| . \|
7	0.10048	\| . \|** . \|
8	0.12872	\| . \|***. \|
9	0.03286	\| . \|* . \|
10	0.16034	\| . \|***. \|
11	-0.03794	\| . *\| . \|
12	-0.14469	\| .***\| . \|
13	0.06415	\| . \|* . \|
14	0.15482	\| . \|***. \|
15	-0.10989	\| . **\| . \|

The ARIMA Procedure

Autocorrelation Check for White Noise
To Lag	Chi-Square	DF	Pr > ChiSq	Autocorrelations
6	87.22	6	<.0001	0.440	0.430	0.458	0.309	0.326	0.204
12	131.39	12	<.0001	0.259	0.292	0.218	0.337	0.240	0.150

The second IDENTIFY statement differences the series. The results of the second IDENTIFY statement are shown in Output 7.1.2. This output shows autocorrelation, inverse autocorrelation, and partial autocorrelation functions typical of MA(1) processes.

Output 7.1.2: Output from the Second IDENTIFY Statement

The ARIMA Procedure

Name of Variable = u
Period(s) of Differencing	1
Mean of Working Series	0.019752
Standard Deviation	1.160921
Number of Observations	99
Observation(s) eliminated by differencing	1

Autocorrelations
Lag	Covariance	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1	Std Error
0	1.347737	1.00000	\| \|********************\|	0
1	-0.699404	-.51895	\| **********\| . \|	0.100504
2	-0.036142	-.02682	\| . *\| . \|	0.124666
3	0.245093	0.18186	\| . \|****. \|	0.124724
4	-0.234167	-.17375	\| . ***\| . \|	0.127374
5	0.181778	0.13488	\| . \|*** . \|	0.129746
6	-0.184601	-.13697	\| . ***\| . \|	0.131155
7	0.0088659	0.00658	\| . \| . \|	0.132592
8	0.146372	0.10861	\| . \|** . \|	0.132595
9	-0.241579	-.17925	\| .****\| . \|	0.133490
10	0.240512	0.17846	\| . \|****. \|	0.135900
11	0.031005	0.02301	\| . \| . \|	0.138247
12	-0.250954	-.18620	\| . ****\| . \|	0.138285
13	0.095295	0.07071	\| . \|* . \|	0.140795
14	0.194110	0.14403	\| . \|*** . \|	0.141153
15	-0.219688	-.16300	\| . ***\| . \|	0.142630

"." marks two standard errors

The ARIMA Procedure

Inverse Autocorrelations
Lag	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
1	0.72538	\| . \|*************** \|
2	0.48987	\| . \|********** \|
3	0.35415	\| . \|******* \|
4	0.34169	\| . \|******* \|
5	0.33466	\| . \|******* \|
6	0.34003	\| . \|******* \|
7	0.24192	\| . \|***** \|
8	0.12899	\| . \|***. \|
9	0.06597	\| . \|* . \|
10	0.01654	\| . \| . \|
11	0.06434	\| . \|* . \|
12	0.08659	\| . \|** . \|
13	0.02485	\| . \| . \|
14	-0.03545	\| . *\| . \|
15	-0.00113	\| . \| . \|

Partial Autocorrelations
Lag	Correlation	-1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 1
1	-0.51895	\| **********\| . \|
2	-0.40526	\| ********\| . \|
3	-0.07862	\| . **\| . \|
4	-0.14588	\| .***\| . \|
5	0.02735	\| . \|* . \|
6	-0.13782	\| .***\| . \|
7	-0.16741	\| .***\| . \|
8	-0.06041	\| . *\| . \|
9	-0.18372	\| ****\| . \|
10	-0.01478	\| . \| . \|
11	0.14277	\| . \|***. \|
12	-0.04345	\| . *\| . \|
13	-0.19959	\| ****\| . \|
14	0.08302	\| . \|** . \|
15	0.00278	\| . \| . \|

The ARIMA Procedure

Autocorrelation Check for White Noise
To Lag	Chi-Square	DF	Pr > ChiSq	Autocorrelations
6	38.13	6	<.0001	-0.519	-0.027	0.182	-0.174	0.135	-0.137
12	50.62	12	<.0001	0.007	0.109	-0.179	0.178	0.023	-0.186

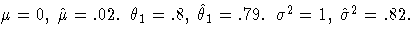The ESTIMATE statement fits an ARIMA(0,1,1) model to the simulated data. Note that in this case the parameter estimates are reasonably close to the values used to generate the simulated data. ( ${{\mu}=0, \hat{{\mu}}=.02. {\theta}_{1}=.8, \hat{{\theta}}_{1}=.79. {\sigma}^2=1, \hat{{\sigma}}^2=.82.}$ )

The ESTIMATE statement results are shown in Output 7.1.3.

Output 7.1.3: Output from Fitting ARIMA(0,1,1) Model

The ARIMA Procedure

Conditional Least Squares Estimation
Parameter	Estimate	Approx Std Error	t Value	Pr > \|t\|	Lag
MU	0.02056	0.01972	1.04	0.2997	0
MA1,1	0.79142	0.06474	12.22	<.0001	1

Constant Estimate	0.020558
Variance Estimate	0.819807
Std Error Estimate	0.905432
AIC	263.2594
SBC	268.4497
Number of Residuals	99

* AIC and SBC do not include log determinant.

Correlations of Parameter Estimates
Parameter	MU	MA1,1
MU	1.000	-0.124
MA1,1	-0.124	1.000

Autocorrelation Check of Residuals
To Lag	Chi-Square	DF	Pr > ChiSq	Autocorrelations
6	6.48	5	0.2623	-0.033	0.030	0.153	-0.096	0.013	-0.163
12	13.11	11	0.2862	-0.048	0.046	-0.086	0.159	0.027	-0.145
18	20.12	17	0.2680	0.069	0.130	-0.099	0.006	0.164	-0.013
24	24.73	23	0.3645	0.064	0.032	0.076	-0.077	-0.075	0.114

Model for variable u
Estimated Mean	0.020558
Period(s) of Differencing	1

Moving Average Factors
Factor 1:	1 - 0.79142 B**(1)

Chapter Contents
Previous
Next
Top