Example 8.1: Analysis of Real Output Series

The AUTOREG Procedure

Example 8.1: Analysis of Real Output Series

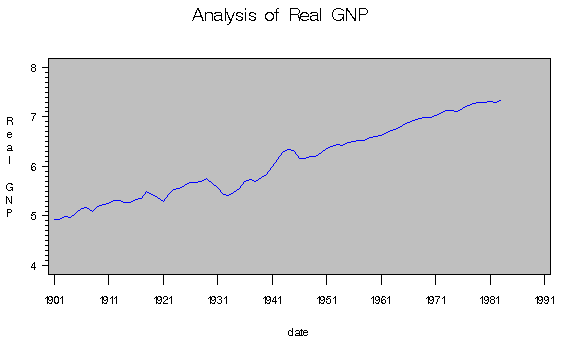
In this example, the annual real output series is analyzed over the period 1901 to 1983 (Gordon 1986, pp 781-783). With the DATA step, the original data is transformed using the natural logarithm, and the differenced series DY is created for further analysis. The log of real output is plotted in Output 8.1.1.


   title 'Analysis of Real GNP';
   data gnp;
      date = intnx( 'year', '01jan1901'd, _n_-1 );
      format date year4.;
      input x @@;
      y  = log(x);
      dy = dif(y);
      t  = _n_;
      label y  = 'Real GNP'
            dy = 'First Difference of Y'
            t  = 'Time Trend';
   datalines;
   ... datalines omitted ...
   ;
   
   proc gplot data=gnp;
      plot y * date /
          haxis='01jan1901'd '01jan1911'd '01jan1921'd '01jan1931'd
                '01jan1941'd '01jan1951'd '01jan1961'd '01jan1971'd
                '01jan1981'd '01jan1991'd;
      symbol i=join;
   run;

Output 8.1.1: Real Output Series: 1901 - 1983

The (linear) trend-stationary process is estimated using the following form:

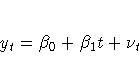
$y_{t} = {\beta}_{0} + {\beta}_{1} t + {\nu}_{t}$

where

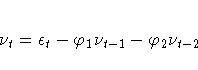
${\nu}_{t} = {\epsilon}_{t} - {\varphi}_{1} {\nu}_{t-1} - {\varphi}_{2} {\nu}_{t-2}$

${\epsilon}_{t} {\sim} \rm{IN}(0, {\sigma}_{{\epsilon}})$

The preceding trend-stationary model assumes that uncertainty over future horizons is bounded since the error term, ${{\nu}_{t}}$ , has a finite variance. The maximum likelihood AR estimates are shown in Output 8.1.2.


   proc autoreg data=gnp;
      model y = t / nlag=2 method=ml;
   run;

Output 8.1.2: Estimating the Linear Trend Model

The AUTOREG Procedure

Maximum Likelihood Estimates
SSE	0.23954331	DFE	79
MSE	0.00303	Root MSE	0.05507
SBC	-230.39355	AIC	-240.06891
Regress R-Square	0.8645	Total R-Square	0.9947
Durbin-Watson	1.9935

Variable	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|	Variable Label
Intercept	1	4.8206	0.0661	72.88	<.0001
t	1	0.0302	0.001346	22.45	<.0001	Time Trend
AR1	1	-1.2041	0.1040	-11.58	<.0001
AR2	1	0.3748	0.1039	3.61	0.0005

Autoregressive parameters assumed given.
Variable	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|	Variable Label
Intercept	1	4.8206	0.0661	72.88	<.0001
t	1	0.0302	0.001346	22.45	<.0001	Time Trend

Nelson and Plosser (1982) failed to reject the hypothesis that macroeconomic time series are nonstationary and have no tendency to return to a trend line. In this context, the simple random walk process can be used as an alternative process:

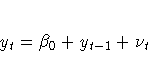
$y_{t} = {\beta}_{0} + y_{t-1} + {\nu}_{t}$

where ${ {\nu}_{t}= {\epsilon}_{t}}$ and y₀=0. In general, the difference-stationary process is written as

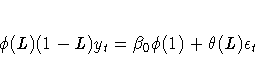
${\phi}(L)(1-L) y_{t} = {\beta}_{0}{\phi}(1) + {\theta}(L) {\epsilon}_{t}$

where L is the lag operator. You can observe that the class of a difference-stationary process should have at least one unit root in the AR polynomial ${{\phi}(L)(1-L)}$ .

The Dickey-Fuller procedure is used to test the null hypothesis that the series has a unit root in the AR polynomial. Consider the following equation for the augmented Dickey-Fuller test:

${\Delta} y_{t} = {\beta}_{0} + {\delta}t + {\beta}_{1} y_{t-1} + \sum_{i=1}^m{{\gamma}_{i}{\Delta} y_{t-i}} + {\epsilon}_{t}$

where ${{\Delta}=1-L}$ . The test statistic ${ {\tau}_{{\tau}}}$ is the usual t ratio for the parameter estimate ${ \hat{{\beta}}_{1}}$ , but the ${ {\tau}_{{\tau}}}$ does not follow a t distribution.

The %DFTEST macro computes the test statistic ${ {\tau}_{{\tau}}}$ and its p value to perform the Dickey-Fuller test. The default value of m is 3, but you can specify m with the AR= option. The option TREND=2 implies that the Dickey-Fuller test equation contains linear time trend. See Chapter 4, "SAS Macros and Functions," for details.


   %dftest(gnp,y,trend=2,outstat=stat1)
   
   proc print data=stat1;
   run;

The augmented Dickey-Fuller test indicates that the output series may have a difference-stationary process. The statistic _TAU_ has a value of -2.61903 and its p-value is 0.29104. See Output 8.1.3.

Output 8.1.3: Augmented Dickey-Fuller Test Results

Obs	_TYPE_	_STATUS_	_DEPVAR_	_NAME_	_MSE_	Intercept	AR_V	time	DLAG_V	AR_V1	AR_V2	AR_V3	_NOBS_	_TAU_	_TREND_	_DLAG_	_PVALUE_
1	OLS	0 Converged	AR_V		.003198469	0.76919	-1	0.004816233	-0.15629	0.37194	0.025483	-0.082422	79	-2.61903	2	1	0.27321
2	COV	0 Converged	AR_V	Intercept	.003198469	0.08085	.	0.000513286	-0.01695	0.00549	0.008422	0.010556	79	-2.61903	2	1	0.27321
3	COV	0 Converged	AR_V	time	.003198469	0.00051	.	0.000003387	-0.00011	0.00004	0.000054	0.000068	79	-2.61903	2	1	0.27321
4	COV	0 Converged	AR_V	DLAG_V	.003198469	-0.01695	.	-.000108543	0.00356	-0.00120	-0.001798	-0.002265	79	-2.61903	2	1	0.27321
5	COV	0 Converged	AR_V	AR_V1	.003198469	0.00549	.	0.000035988	-0.00120	0.01242	-0.003455	0.002095	79	-2.61903	2	1	0.27321
6	COV	0 Converged	AR_V	AR_V2	.003198469	0.00842	.	0.000054197	-0.00180	-0.00346	0.014238	-0.002910	79	-2.61903	2	1	0.27321
7	COV	0 Converged	AR_V	AR_V3	.003198469	0.01056	.	0.000067710	-0.00226	0.00209	-0.002910	0.013538	79	-2.61903	2	1	0.27321

The AR(1) model for the differenced series DY is estimated using the maximum likelihood method for the period 1902 to 1983. The difference-stationary process is written

${\Delta} y_{t} = {\beta}_{0} + {\nu}_{t}$

${\nu}_{t} = {\epsilon}_{t} - {\varphi}_{1} {\nu}_{t-1}$

The estimated value of ${\varphi}_{1}$ is -0.297 and that of ${{\beta}_{0}}$ is 0.0293. All estimated values are statistically significant.


   proc autoreg data=gnp;
      model dy = / nlag=1 method=ml;
   run;

Output 8.1.4: Estimating the Differenced Series with AR(1) Error

The AUTOREG Procedure

Maximum Likelihood Estimates
SSE	0.27107673	DFE	80
MSE	0.00339	Root MSE	0.05821
SBC	-226.77848	AIC	-231.59192
Regress R-Square	0.0000	Total R-Square	0.0900
Durbin-Watson	1.9268

Variable	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|
Intercept	1	0.0293	0.009093	3.22	0.0018
AR1	1	-0.2967	0.1067	-2.78	0.0067

Autoregressive parameters assumed given.
Variable	DF	Estimate	Standard Error	t Value	Approx Pr > \|t\|
Intercept	1	0.0293	0.009093	3.22	0.0018

Chapter Contents
Previous
Next
Top