Criteria for Optimality

Chapter Contents

The NLP Procedure

Criteria for Optimality

PROC NLP solves

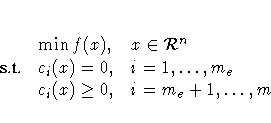
$& \min f(x) , & x \in {\cal R}^n \ {s.t.} & c_i(x) = 0 , & i = 1, ... ,m_e \ & c_i(x) \ge 0 , & i = m_e+1, ... ,m$

where f is the objective function and the m c_i's are the constraint functions.

A point x is feasible if it satisfies all the constraints. The feasible region G is the set of all the feasible points. x^* is a global solution of the preceeding problem if no point in G has a lower function value than f(x^*). x^* is a local solution of the problem if there exists some open neighborhood surrounding x^* in that no point has a lower function value than f(x^*). Nonlinear Programming algorithms cannot consistently find global minima. All the algorithms in PROC NLP find a local minimum for this problem. If you need to check whether the obtained solution is a global minimum, you may have to run PROC NLP with different starting points obtained either at random or by selecting a point on a grid that contains G.

The local minimizer x^* of this problem satisfies the following local optimality conditions:

The grdient (vector of first derivatives) $g(x^*) = \nabla f(x^*)$ of the objective function f (projected toward the feasible region if the problem is constrained) at the point x^* is zero.
The Hessian (matrix of second derivatives) $G(x^*) = \nabla^2 f(x^*)$ of the objective function f (projected toward the feasible region G in the constrained case) at the point x^* is positive definite.

Most of the optimization algorithms in PROC NLP use iterative techniques that result in a sequence of points x⁰,...,xⁿ,..., that converges to a local solution x^*. At the solution, PROC NLP performs tests to confirm that the (projected) gradient is close to zero and that the (projected) Hessian matrix is positive definite.

Karush-Kuhn-Tucker Conditions

An important tool in the analysis and design of algorithms in constrained optimization is the Lagrangian Function, that is a linear combination of the objective function and the constraints:

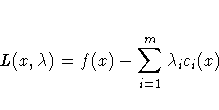
$L(x,\lambda) = f(x) - \sum_{i=1}^m \lambda_i c_i(x)$

The coefficients $\lambda_i$ are called Lagrange multipliers. This tool makes it possible to state necessary and sufficient conditions for a local minimum. The various algorithms in PROC NLP create sequences of points, each of that is closer than the previous one to satisfying these conditions.

Assuming that the functions f and c_i are twice continuously differentiable, the point x^* is a local minimum of the nonlinear programming problem, if there exists a vector $\lambda^*=(\lambda_1^*, ... ,\lambda_m^*)$ that meets the following conditions.

1. first-order, Karush-Kuhn-Tucker conditions:

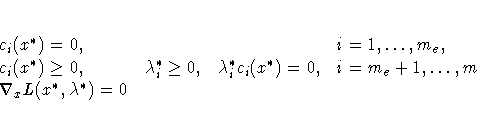
$c_i(x^*) = 0 , & & & i = 1, ... ,m_e, \ c_i(x^*) \ge 0 , & \lambda_i^* \ge 0,... ...^* c_i(x^*) = 0 , & i = m_e+1, ... ,m \ \nabla_x L(x^*,\lambda^*) = 0 & & &$

2. Second-order conditions:

Each nonzero vector $y \in {\cal R}^n$ for which

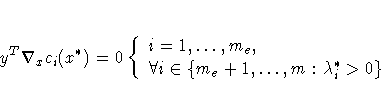
$y^T \nabla_x c_i(x^*) = 0 \{ i = 1, ... ,m_e , \ \forall i\in \{ m_e+1, ... ,m: \lambda_i^* \gt 0 \} .$

satisfies

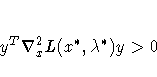
$y^T \nabla_x^2 L(x^*,\lambda^*) y \gt 0$

Most of the algorithms to solve this problem attempt to find a combination of vectors x and $\lambda$ for which the gradient of the Langrangian function in respect to x is zero.

Derivatives

The first and second order conditions of optimality are based on first and second derivates of the object function f and the constraints c_i.

The gradient vector contains the first derivatives of the objective function f with respect to the parameters x₁, ... ,x_n, as follows:

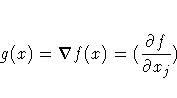
$g(x) = \nabla f(x) = (\frac{\partial f}{\partial x_j})$

The n ×n symmetric Hessian matrix contains the second derivatives of the objective function f with respect to the parameters x₁, ... ,x_n, as follows:

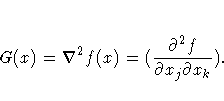
$G(x) = \nabla^2 f(x) = (\frac{\partial^2 f}{\partial x_j \partial x_k}) .$

For Least-Squares problems, the m ×n Jacobian matrix contains the first-order derivatives of m objective functions f_i(x) with respect to the parameters x₁, ... ,x_n, as follows:

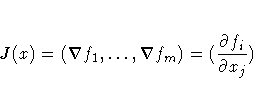
$J(x) = (\nabla f_1, ... ,\nabla f_m) = (\frac{\partial f_i}{\partial x_j})$

In case of Least-Squares problems, the crossproduct Jacobian J^TJ,

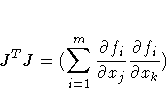
$J^TJ = ({\sum_{i=1}^m \frac{\partial f_i}{\partial x_j} \frac{\partial f_i}{\partial x_k}})$

is used as an approximate Hessian matrix. It is a very good approximation of the Hessian if the residuals at the solution are "small." (If the residuals are not sufficiently small at the solution, this approach may result in slow convergence.) The fact that it is possible to obtain Hessian approximations for this problem that do not require any computation of second derivatives means that Least-Squares algorithms are more efficient than unconstrained optimization algorithms. Using the vector f = f(x) of function values, f(x) = (f₁(x), ... ,f_m(x))^T, PROC NLP computes the gradient g=g(x) by

g(x) = J^T(x) f(x)

The mc ×n Jacobian matrix contains the first-order derivatives of mc nonlinear constraint functions c_i(x), i = 1, ... ,mc, with respect to the parameters x₁, ... ,x_n, as follows:

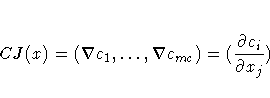
$CJ(x) = (\nabla c_1, ... ,\nabla c_{mc}) = (\frac{\partial c_i}{\partial x_j})$

PROC NLP provides three ways to compute derivatives:

It computes analytical first- and second-order derivatives of the objective function f with respect to the n variables x_j.
It computes first- and second-order finite difference approximations to the derivatives. For more information, see the section "Finite-Difference Approximations of Derivatives".
The user supplies formulas for analytical or numerical first- and second-order derivatives of the objective function in the GRADIENT, JACOBIAN, CRPJAC, and HESSIAN statements. The JACNLC statement can be used to specify the derivatives for the nonlinear constraints.

Chapter Contents
Previous
Next
Top