Computational Problems
First Iteration Overflows
If you use bad initial values for the parameters, the
computation of the value of the objective function (and
its derivatives) can lead to arithmetic overflows in the
first iteration.
The line-search algorithms that work with cubic extrapolation
are especially sensitive to arithmetic overflows. If an
overflow occurs with an optimization technique that uses
line-search, you can use the INSTEP= option to reduce the
length of the first trial step during the line-search of the
first five iterations or use the DAMPSTEP or MAX STEP
option to restrict the step length of the initial 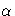 in subsequent iterations. If an arithmetic overflow occurs in
gthe first iteration of the trust-region, double dogleg, or
Levenberg-Marquardt algorithm, you can use the INSTEP= option
to reduce the default trust region radius of the first iteration.
You can also change the minimization technique or the line-search
method. If none of these methods helps, consider the following
actions:
in subsequent iterations. If an arithmetic overflow occurs in
gthe first iteration of the trust-region, double dogleg, or
Levenberg-Marquardt algorithm, you can use the INSTEP= option
to reduce the default trust region radius of the first iteration.
You can also change the minimization technique or the line-search
method. If none of these methods helps, consider the following
actions:
- scale the parameters
- provide better initial values
- use boundary constraints to avoid the region
where overflows may happen
- change the algorithm (specified in program
statements) which computes the objective function
Problems in Evaluating the Objective Function
The starting point x(0) must be a point that can be evaluated by
all the functions involved in your problem.
However, during optimization the optimizer may
iterate to a point x(k) where
the objective function or nonlinear constraint
functions and their derivatives cannot be evaluated.
If you can identify the problematic region,
you can prevent the algorithm from reaching it by adding another
constraint to the problem. Another possiblity is a modification
of the objective function, that will, as a result, get a large, undesired
function value. As a result, the optimization algorithm
reduces the step length and stays closer to the point that
has been evaluated successfully in the previous iteration.
For more information, refer to the section "Missing Values in Program Statements".
Problems with Quasi-Newton Methods for Nonlinear Constraints
The sequential quadratic programming algorithm in QUANEW,
that is used for solving nonlinearly constrained problems,
can have problems updating the Lagrange multiplier vector
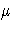 . This results usually in very high values of the
Lagrange function and in watchdog restarts indicated
in the iteration history. If this happens,
there are three actions you can try:
. This results usually in very high values of the
Lagrange function and in watchdog restarts indicated
in the iteration history. If this happens,
there are three actions you can try:
- By default, the Lagrange vector
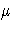 is evaluated in the same way as Powell (1982) describes.
This corresponds to VERSION=2.
By specifying VERSION=1, a modification of this
algorithm replaces the update of the Lagrange vector
is evaluated in the same way as Powell (1982) describes.
This corresponds to VERSION=2.
By specifying VERSION=1, a modification of this
algorithm replaces the update of the Lagrange vector 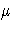 with
the original update of Powell (1978),
that
is used in VF02AD.
with
the original update of Powell (1978),
that
is used in VF02AD.
- You can use the INSTEP= option to
impose an upper bound for the step size
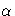 during
the first five iterations.
during
the first five iterations.
- You can use the INHESSIAN[=r] option to specify a
different starting approximation for the Hessian.
Choosing simply the INHESSIAN option will use the Cholesky
factor of a (possibly ridged) finite difference approximation
of the Hessian to initialize the quasi-Newton update process.
Other Convergence Difficulties
There are a number of things to try if the optimizer fails to
converge.
- Check the derivative specification:
If derivatives are specified by using the GRADIENT, HESSIAN,
JACOBIAN, CRPJAC, or JACNLC statement, you can compare the
specified derivatives with those computed by finite-difference
approximations (specifying the FD and FDHESSIAN option).
Use the GRADCHECK option to check if the gradient g
is correct. For more information, refer to the section "Testing the Gradient Specification".
- Forward-difference derivatives specified with the FD[=]
or FDHESSIAN[=] option may not be precise enough to satisfy
strong gradient termination criteria. You may need to specify
the more expensive central-difference formulas or use
analytical derivatives.
The finite difference intervals
may be too small or too big and the finite difference
derivatives may be erroneous. You can specify the FDINT=
option to compute better finite difference intervals.
- Change the optimization technique:
For example, if you use the default TECH=LEVMAR, you can
- change to TECH=QUANEW or to TECH=NRRIDG
- run some iterations with TECH= CONGRA, write the results
in an OUTEST= or OUTVAR= data set, and use them as initial
values specified by an INEST= or INVAR= data
set in a second run with a different TECH= technique
- Change or modify the update technique
and the line-search algorithm:
This method applies only to TECH=QUANEW, TECH=HYQUAN, or TECH= CONGRA.
For example, if you use the default update formula and the
default line-search algorithm, you can
- change the update formula with the UPDATE= option
- change the line-search algorithm with the LIS= option
- specify a more precise line-search with the
LSPRECISION= option, if you use LIS=2 or LIS=3
- Change the initial values by using a grid search specification
to obtain a set of good feasible starting values.
Convergence to Stationary Point
The (projected) gradient at a stationary point is zero and that translates into
a zero step size. The stopping criteria are satisfied.
There are two ways to avoid this situation:
- Use the PARMS statement to specify a grid of
feasible starting points.
- Use the OPTCHECK[=r] option to
avoid terminating at the stationary point.
The signs of the eigenvalues of the (reduced) Hessian matrix
contain information regarding a stationary point.
- If all eigenvalues are positive,
the Hessian matrix is positive definite and
the point is a minimum point.
- If some of the eigenvalues are positive and all
remaining eigenvalues are zero,
the Hessian matrix is positive semidefinite and
the point is a minimum or saddle point.
- If all eigenvalues are negative,
the Hessian matrix is negative definite and
the point is a maximum point.
- If some of the eigenvalues are negative and all
remaining eigenvalues are zero,
the Hessian matrix is negative semidefinite and
the point is a maximum or saddle point.
- If all eigenvalues are zero,
the point can be a minimum, maximum, or saddle point.
Precision of Solution
In some applications, PROC NLP may result in parameter
estimates that are not precise enough. Usually this means
that the procedure terminated too early at a point
too far from the optimal point. The termination
criteria define the size of the termination region around the
optimal point. Any point inside this region can be accepted for
terminating the optimization process.
The default values of the termination criteria are set to satisfy
a reasonable compromise between the computational effort (computer
time) and the precision of the computed estimates for the most
common applications. However, there are a number of circumstances
where the default values of the termination criteria
specify a region that is either too large or is too small.
If the termination region is too large, then it can contain
points with low precision.
In such cases, you should inspect
your log or list output to find the message stating which
termination criterion terminated the optimization process.
In many applications, you can obtain a solution with higher
precision by simply using the old parameter estimates as
starting values in a subsequent run where you specify a
smaller value for the termination criterion that was
satisfied at the former run.
If the termination region is too small,
the optimization process may take longer
to find a point inside such a region or cannot even find such
a point due to rounding errors in function values and
derivatives. This can easily happen in applications where
finite difference approximations of derivatives are used
and the GCONV and ABSGCONV termination criteria are too
small to respect rounding errors in the gradient values.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.