Input and Output Data Sets
The DATA= data set is used only to specify an objective function
f, that is a combination of m other functions fi. For each
function fi, i = 1, ... ,m, listed in a MAX, MIN, or LSQ
statement, each observation l, l = 1, ... ,nobs, in the DATA=
data set defines a specific function fil that is evaluated
by substituting the values of the variables of this observation
into the program statements. If the MAX or MIN statement is used,
the m * nobs specific functions fil are added to a single
objective function f. If the LSQ statement is used, the
sum-of-squares f of the m * nobs specific functions fil
is minimized.
The NOMISS option causes observations with missing values to
be skipped.
The INEST= (or INVAR=, or ESTDATA=) input data set can be used
to specify the initial values of the parameters defined in a
PARMS statement as well as boundary constraints and the
more general linear constraints which could be imposed on these
parameters. This form of input is similar to the dense format
input used in PROC LP.
The variables of the INEST= data set are
- a character variable _TYPE_ that indicates the type of
the observation
- n numeric variables with the parameter names used in
the PARMS statement
- the BY variables that are used in a DATA= input data set
- a numeric variable _RHS_ (right-hand side)
(needed only if linear constraints are used)
- additional variables with names corresponding to constants
used in the program statements
The content of the _TYPE_ variable defines the meaning of the
observation of the INEST= data set. PROC NLP recognizes
the following _TYPE_ values:
- PARMS, which specifies initial values for parameters.
Additional variables can contain the
values of constants that are referred to in program
statements.
The values of the constants in the PARMS observation
initialize the constants in the program statements.
- UPPERBD | UB, which as specifies upper bounds.
Missing values indicate that no upper
bound is specified for the parameter.
- LOWERBD | LB, which specifies lower bounds.
Missing values indicate that no lower
bound is specified for the parameter.
- LE | <= | <, which specifies linear constraint
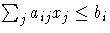 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
- GE | >= | >, which specifies linear constraint
 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing value indicates zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing value indicates zeros.
- EQ | =, which specifies linear constraint
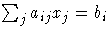 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing value indicates zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing value indicates zeros.
The constraints specified in an INEST= data set are
added to the constraints specified in BOUNDS and LINCON statements.
You can use an OUTEST= data set
as an INEST= data set in a subsequent run of PROC NLP.
However, be aware that the OUTEST= data set also
contains the boundary and general
linear constraints specified in the former run of PROC NLP. When
you are using this OUTEST= data set without changes as an INEST=
data set, PROC NLP adds the constraints from the data set to the
constraints specified by a BOUNDS and LINCON statement. Although
PROC NLP automatically eliminates multiple identical constraints
you should avoid specifying the same constraint a second time.
Two types of INQUAD= data sets can be used to specify the
objective function of a quadratic programming problem
for TECH=QUADAS or TECH=LICOMP,
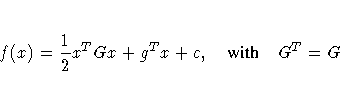
The dense INQUAD= data set must contain all numerical
values of the symmetric matrix G, vector g, and the value
of the scalar c.
Using the sparse INQUAD= data set allows to specify
only the nonzero positions in matrix G and vector g.
Those locations that are not set by the sparse
INQUAD= data set are assumed to be zero.
Dense INQUAD= Data Set
A dense INQUAD= data set must contain two character
variables _TYPE_ and _NAME_ and at least n numeric
variables whose names are the parameter names.
The _TYPE_ variable takes
the following values:
- QUAD lists the n values of the row of
the G matrix that is defined by the parameter name
used in the _NAME_ variable.
- LINEAR lists the n values of the g
vector.
- CONST sets the the value of the scalar c and
cannot contain different numerical
values; however, it could contain up to n-1 missing values.
- PARMS specifies initial values for parameters.
- UPPERBD | UB
specifies upper bounds.
Missing value indicates that no upper
bound is specified.
- LOWERBD | LB
specifies lower bounds.
The use of a missing value indicates that no lower
bound.
- LE | <= | <
specifies linear constraint
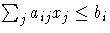 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
- GE | >= | >
specifies linear constraint
 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
- EQ | =
specifies linear constraint
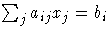 . The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
. The n parameter values contain the coefficients aij,
and the _RHS_ variable contains the right-hand side bi.
Missing values indicate zeros.
Constraints specified in a dense INQUAD= data set are
added to the constraints specified in BOUNDS and LINCON
statements.
Sparse INQUAD= Data Set
A sparse INQUAD= data set must contain three character
variables _TYPE_, _ROW_, and _COL_ and one numeric
variable _VALUE_.
The _TYPE_ variable can assume
three values:
- QUAD specifies that the _ROW_ and _COL_
variables define the row and column location of the
value in the G matrix.
- LINEAR specifies that the _ROW_
variable defines the row location of the value in the
g vector. The _COL_ variable is not used.
Using both the MODEL= option and the INCLUDE program
statement with the same model file will include the
file twice (erroneous in most cases).
OUT= Output Data Set
The OUT= data set contains those variables of a DATA= input
data set that are referred to in the program statements
and additionally variables computed by the
program statements for the objective function. Specifying
the NOMISS option enables you to skip observations with
missing values in variables used in the program
statements.
The OUT= data set can also contain
first- and second-order derivatives of these variables
if the OUTDER= option is specified. The variables and
derivatives are the
final parameter estimates x* or (for TECH=NONE)
the initial value x0.
The variables of the OUT= data set are:
- the BY variables and all other variables that are used in
a DATA= input data set and referred to in the program code
- a variable _OBS_ containing the number of observations
read from a DATA= input data set where the counting is
restarted with the start of each BY group. If there is
no DATA= input data set, then _OBS_=1
- a character variable _TYPE_ naming the type of
the observation
- the parameter variables listed in the PARMS statement
- the function variables listed in the the MIN, MAX, or
LSQ statement
- all other variables computed in the program statements
- the character variable _WRT_ (if OUTDER=1) containing
the with respect to variable for which the
first-order derivatives are written in the function
variables
- the two character variables _WRT1_ and _WRT2_(if OUTDER=2)
containing the two with respect to variables for
which the first- and second-order derivatives are written
in the function variables
OUTEST= Output Data Set
The OUTEST= or OUTVAR= output data set saves the
optimization solutions of the use of the OUTEST= or OUTVAR= data set
- to save the values of the objective function on grid points
to examine, for example, surface plots using PROC G3D
(use the OUTGRID option)
- to avoid any costly computation of analytical (first- or
second-order) derivatives during optimization when they
only needed upon termination. In this case a
two-step approach is recommended:
- In a first execution, the optimization is done;
that is, optimal parameter estimates are computed, and
the results are saved in an OUTEST= data set.
- In a subsequent execution, the optimal parameter
estimates in the former OUTEST= data set are
read in an INEST= data set and used with
TECH=NONE to compute further results, such as analytical
second-order derivatives or some kind of covariance
matrix.
- to restart the procedure using parameter estimates
as initial values
- to split a timeconsuming optimization problem into a series
of smaller problems using intermediate results as
initial values in a subsequent runs.
(Refer to the MAXTIME=, MAXIT=, and MAXFU= options to trigger stopping
in the section "PROC NLP Statement")
- to write the value of the objective function,
the parameter estimates, the time in
seconds starting at the beginning of the optimization process
and (if available) the gradient to the OUTEST=
data set during the iterations. After the PROC NLP run
is completed, the convergence progress can be inspected
by graphically displaying the iterative information.
(Refer to the OUTITER option in the section "PROC NLP Statement")
The variables of the OUTEST= data set are
- the BY variables that are used in
a DATA= input data set
- a character variable _TECH_ naming the
optimization technique used
- a character variable _TYPE_ specifying the type of
the observation
- a character variable _NAME_ naming
the observation. For a linear constraint, the _NAME_
variable indicates whether the constraint is active
at the solution. For the initial observations, the
_NAME_ variable indicates if the number in the _RHS_
variable corresponds to the number of positive,
negative, or zero eigenvalues
- n numeric variables with the parameter names used in
the PARMS statement. These variables contain a
point x of the parameter space, lower or upper boundary
constraints, or the coefficients of linear constraints
- a numeric variable _RHS_ (right-hand side) that is used
for the right-hand side value bi of a linear constraints
or for the value f=f(x) of the objective function at a
point x of the parameter space
- a numeric variable _ITER_, that is zero for initial
values, equal to the iteration number for the OUTITER
output, and missing for the result output
The _TYPE_ variable identifies how to interpret the observation.
If _TYPE_ is:
- PARMS then parameter named variables contain the coordinates
of the resulting point x*.
The _RHS_ variable contains f(x*).
- INITIAL then parameter named variables contain the
feasible starting point x(0).
The _RHS_ variable contains f(x(0)).
- GRIDPNT then (if the OUTGRID option is specified)
parameter named variables contain the coordinates
of any point x(k) used in the grid search.
The _RHS_ variable contains f(x(k)).
- GRAD then parameter named variables
contain the gradient at the initial or final estimates.
- STDERR then parameter named variables contain
the approximate standard errors (square roots of the
diagonal elements of the covariance matrix) if the
COV= option is specified.
- _NOBS_ then (if the COV= options is specified)
all parameter variables contain the value of _NOBS_
used in computing the
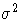 value in the formula
of the covariance matrix.
value in the formula
of the covariance matrix.
- UPPERBD | UB then (if there are boundary constraints)
the parameter variables contain the upper bounds.
- LOWERBD | LB then (if there are boundary constraints)
the parameter variables contain the lower bounds.
- NACTBC then all parameter variables contain the
number nabc of active boundary constraints at the
solution x(*).
- ACTBC then (if there are active boundary constraints)
three observation indicate which
of the parameters is actively constrained, as follows:
- _NAME_=GE
- the active lower bounds
- _NAME_=LE
- the active upper bounds
- _NAME_=EQ
- the active equality constraints
- NACTLC then all parameter variables contain the
number nalc of active linear constraints
that are recognized as linear independent.
- NLDACTLC then all parameter variables contain the
number of active linear
constraints that are recognized
as linearly dependent.
- LE then (if there are linear constraints)
the observation contains the ith linear constraint
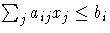 . The parameter variables
contain the coefficients aij, j = 1, ... ,n,
and the _RHS_ variable contains bi. If the
constraint i is active at the solution x*,
then _NAME_= 'ACTLC' or 'LDACTLC'.
. The parameter variables
contain the coefficients aij, j = 1, ... ,n,
and the _RHS_ variable contains bi. If the
constraint i is active at the solution x*,
then _NAME_= 'ACTLC' or 'LDACTLC'.
- GE then (if there are linear constraints)
the observation contains the ith linear constraint
 . The parameter variables
contain the coefficients aij, j = 1, ... ,n,
and the _RHS_ variable contains bi. If the
constraint i is active at the solution x*,
then _NAME_= 'ACTLC' or 'LDACTLC'.
. The parameter variables
contain the coefficients aij, j = 1, ... ,n,
and the _RHS_ variable contains bi. If the
constraint i is active at the solution x*,
then _NAME_= 'ACTLC' or 'LDACTLC'.
- EQ then (if there are linear constraints)
the observation contains the ith linear constraint
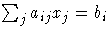 . The parameter variables
contain the coefficients aij, j = 1, ... ,n,
the _RHS_ variable contains bi, and
_NAME_= 'ACTLC' or 'LDACTLC'.
. The parameter variables
contain the coefficients aij, j = 1, ... ,n,
the _RHS_ variable contains bi, and
_NAME_= 'ACTLC' or 'LDACTLC'.
- LAGRANGE then (if at least one of the linear
constraints is an equality constraint or an inequality
constraint that is active)
the observation contains the vector of Lagrange multipliers.
The Lagrange multipliers of active boundary constraints
are listed first followed by those of active linear
constraints and those of active nonlinear constraints.
Lagrange multipliers are only available for the set of
linearly independent active constraints.
- PROJGRAD then (if there are linear constraints)
the observation contains the n - nact values
of the projected gradient gZ = Z'g in the variables
corresponding to the first n-nact parameters.
- JACOBIAN ( then if the PJAC or OUTJAC
option is specified)
the m observations contain the m
rows of the m ×n Jacobian matrix
The _RHS_ variable contains the row number l,
l = 1, ... ,m.
- HESSIAN then the first n observations contain the n
rows of the (symmetric) Hessian matrix.
The _RHS_ variable contains the row number j, j = 1, ... ,n,
and the _NAME_ variable contains the corresponding parameter
name.
- PROJHESS then the first n - nact observations contain
the n-nact rows of the projected Hessian matrix ZTGZ.
The _RHS_ variable contains the row
number j, j = 1, ... ,n-nact, and the _NAME_ variable is
blank.
- CRPJAC then the first n observations contain the n
rows of the (symmetric) crossproduct Jacobian matrix at
the solution.
The _RHS_ variable
contains the row number j, j = 1, ... ,n, and the _NAME_
variable contains the corresponding parameter name.
- PROJCRPJ then the first n - nact observations
contain the n-nact rows of the projected crossproduct
Jacobian matrix ZT(JTJ)Z.
The _RHS_ variable contains the row number j,
j = 1, ... ,n-nact, and the _NAME_ variable is blank.
- COV1, COV2, COV3, COV4, COV5, or COV6 then (depending
on the COV= option) the first n
observations contain the n rows of the (symmetric) covariance
matrix of the parameter estimates.
The _RHS_ variable contains the row
number j, j = 1, ... ,n, and the _NAME_ variable contains
the corresponding parameter name.
- DETERMIN then contains the determinant det = a * 10b of
the matrix specified by the value of the _NAME_ variable
where the value of
the first variable in the PARMS statement and b is in _RHS_.
- NEIGPOS, NEIGNEG, or NEIGZER then
the _RHS_ variable
contains the number of positive, negative, and zero eigenvalues
of the matrix specified by the value of the _NAME_ variable.
- COVRANK then the _RHS_ variable contains the rank
of the covariance matrix.
- SIGSQ then the _RHS_ variable contains the scalar
factor of the covariance matrix.
- _TIME_ then (if the OUTITER option is specified) the
_RHS_ variable contains the number of seconds passed since
the start of the optimization.
- TERMINAT then if optimization terminated at
a point satisfying one of the termination criteria, an
abbreviation of the corresponding criteria is given to
the _NAME_ variable. Otherwise _NAME_='PROBLEMS'.
If for some reason the procedure does not terminate successfully
(for example, no feasible initial values can be
computed or the function value or derivatives at the starting
point cannot be computed), the OUTEST= data set may
contain only part of the observations (usually only the PARMS
and GRAD observation).
Note: Generally you can use an OUTEST= or OUTVAR= data set
as an INEST= or INVAR= data set in a further run of PROC NLP.
However, be aware that the OUTEST= or OUTVAR= data set also
contains the boundary and general
linear constraints specified in the former run of PROC NLP. When
you are using this OUTEST= data set without changes as an INEST=
data set, PROC NLP adds the constraints from the data set to the
constraints specified by a BOUNDS or LINCON statement. Although
PROC NLP automatically eliminates multiple identical constraints
you should avoid specifying the same constraint a second time.
Output of Profiles
The following observations are written to the OUTEST= data set
only when the PROFILE statement or CLPARM option is specified
|
_TYPE_
|
_NAME_
|
_RHS_
|
Meaning of Observation
|
| PLC_LOW | parname | y value | coordinates of lower CL for 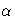 |
| PLC_UPP | parname | y value | coordinates of upper CL for 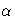 |
| WALD_CL | LOWER | y value | lower Wald CL for 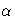 in _ALPHA_ in _ALPHA_ |
| WALD_CL | UPPER | y value | upper Wald CL for 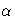 in _ALPHA_ in _ALPHA_ |
| PL_CL | LOWER | y value | lower PL CL for 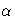 in _ALPHA_ in _ALPHA_ |
| PL_CL | UPPER | y value | upper PL CL for 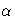 in _ALPHA_ in _ALPHA_ |
| PROFILE | L(THETA) | missing | y value corresponding to x |
| | | | in following _NAME_=THETA |
| PROFILE | THETA | missing | x value corresponding to y |
| | | | in previous _NAME_=L(THETA) |
Assume that the PROFILE statement specifies np parameters and
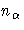 confidence levels. For CLPARM, np=n and
confidence levels. For CLPARM, np=n and
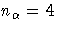 .
.
- _TYPE_=PLC_LOW and _TYPE_=PLC_UPP:
If CLPARM= option or the PROFILE statement with the OUTTABLE option
is specified, then the complete set 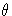 of parameter
estimates (rather than only the confidence limit
of parameter
estimates (rather than only the confidence limit 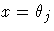 ) is written to the OUTEST= data set for each side of the
confidence interval. This output may be helpful for further
analyses on how small changes in
) is written to the OUTEST= data set for each side of the
confidence interval. This output may be helpful for further
analyses on how small changes in 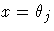 affect the
changes in the other
affect the
changes in the other 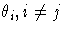 . The _ALPHA_
variable contains the corresponding value of
. The _ALPHA_
variable contains the corresponding value of 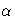 . There should be no more than
. There should be no more than 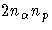 observations.
If the confidence limit cannot be computed, the corresponding
observation is not available.
observations.
If the confidence limit cannot be computed, the corresponding
observation is not available.
- _TYPE_=WALD_CL:
If CLPARM=WALD, CLPARM=BOTH, or the PROFILE statement with
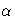 values is specified, then the Wald confidence
limits are written to the OUTEST= data set for each of the
default or specified values of
values is specified, then the Wald confidence
limits are written to the OUTEST= data set for each of the
default or specified values of 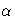 . The _ALPHA_
variable contains the corresponding value of
. The _ALPHA_
variable contains the corresponding value of 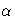 . There should be
. There should be 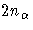 observations.
observations.
- _TYPE_=PL_CL:
If CLPARM=PL, CLPARM=BOTH, or the PROFILE statement with
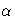 values is specified, then the PL confidence
limits are written to the OUTEST= data set for each of the
default or specified value of
values is specified, then the PL confidence
limits are written to the OUTEST= data set for each of the
default or specified value of 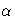 . The _ALPHA_
variable contains the corresponding values of
. The _ALPHA_
variable contains the corresponding values of 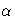 . There should be
. There should be 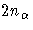 observations; some observations
may have missing values.
observations; some observations
may have missing values.
- _TYPE_=PROFILE:
If CLPARM=PL, CLPARM=BOTH, or the PROFILE statement with
or without 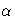 values is specified, then a set of
(x,y) point coordinates in two adjacent observations
with _NAME_=L(THETA) (y value) and _NAME_=THETA
(x value) is written to the OUTEST= data set. The
_RHS_ and _ALPHA_ variables are not used (are set to
missing). The number of observations depends on the difficulty
of the optimization problems.
values is specified, then a set of
(x,y) point coordinates in two adjacent observations
with _NAME_=L(THETA) (y value) and _NAME_=THETA
(x value) is written to the OUTEST= data set. The
_RHS_ and _ALPHA_ variables are not used (are set to
missing). The number of observations depends on the difficulty
of the optimization problems.
OUTMODEL= Output Data Set
The program statements for objective functions, nonlinear
constraints, and derivatives can be saved into an OUTMODEL=
output data set. This data set can be used in an INCLUDE
program statement or as a MODEL= input data set in subsequent
calls of PROC NLP. The OUTMODEL= option is similar to the
option used in PROC MODEL in SAS/ETS software.
Storing Programs in Model Files
Models can be saved to and recalled from
SAS catalog files. SAS catalogs are special files which can store
many kinds of data structures as separate units in one SAS file.
Each separate unit is called an entry, and each entry has an
entry type that identifies its structure to the SAS system.
In general, to save a model, use the OUTMODEL=name option
in the PROC NLP statement, where name is specified as
libref.catalog.entry, libref.entry, or entry.
The libref, catalog, and entry names must be
valid SAS names no more than 8 characters long. The catalog
name is restricted to 7 characters on the CMS operating system.
If not given, the catalog name defaults to MODELS, and the
libref defaults to WORK. The entry type is always MODEL.
Thus, OUTMODEL=X writes the model to the file WORK.MODELS.X.MODEL.
The MODEL= option is used to read in a model. A list of model
files can be specified in the MODEL= option, and a range of names
with numeric suffixes can be given, as in MODEL=(MODEL1-MODEL10).
When more than one model file is given, the list must be placed
in parentheses, as in MODEL=(A B C), except in the case of a
single name. If more than one model file is specified, the files
are combined in the order listed in the MODEL= option.
When the MODEL= option is specified in the PROC NLP statement
and model definition statements are also given later in the
PROC NLP step, the model files are read in first, in the order
listed, and the model program specified in the PROC NLP step
is appended after the model program read from the MODEL= files.
The INCLUDE statement can be used to append model code to the
current model code. The contents of the model files are
inserted into the current model at the position where the
INCLUDE statement appears.
Note that the following statements are not part of the
program code that is written to an OUTMODEL= data set:
MIN, MAX, LSQ, MINQUAD, MAXQUAD, PARMS, BOUNDS, BY,
CRPJAC, GRADIENT, HESSIAN, JACNLC, JACOBIAN, LABEL,
LINCON, MATRIX, NLINCON.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
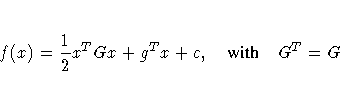
![]() confidence levels. For CLPARM, np=n and
confidence levels. For CLPARM, np=n and
![]() .
.![]() of parameter
estimates (rather than only the confidence limit
of parameter
estimates (rather than only the confidence limit ![]() ) is written to the OUTEST= data set for each side of the
confidence interval. This output may be helpful for further
analyses on how small changes in
) is written to the OUTEST= data set for each side of the
confidence interval. This output may be helpful for further
analyses on how small changes in ![]() affect the
changes in the other
affect the
changes in the other ![]() . The _ALPHA_
variable contains the corresponding value of
. The _ALPHA_
variable contains the corresponding value of ![]() . There should be no more than
. There should be no more than ![]() observations.
If the confidence limit cannot be computed, the corresponding
observation is not available.
observations.
If the confidence limit cannot be computed, the corresponding
observation is not available.
![]() values is specified, then the Wald confidence
limits are written to the OUTEST= data set for each of the
default or specified values of
values is specified, then the Wald confidence
limits are written to the OUTEST= data set for each of the
default or specified values of ![]() . The _ALPHA_
variable contains the corresponding value of
. The _ALPHA_
variable contains the corresponding value of ![]() . There should be
. There should be ![]() observations.
observations.
![]() values is specified, then the PL confidence
limits are written to the OUTEST= data set for each of the
default or specified value of
values is specified, then the PL confidence
limits are written to the OUTEST= data set for each of the
default or specified value of ![]() . The _ALPHA_
variable contains the corresponding values of
. The _ALPHA_
variable contains the corresponding values of ![]() . There should be
. There should be ![]() observations; some observations
may have missing values.
observations; some observations
may have missing values.
![]() values is specified, then a set of
(x,y) point coordinates in two adjacent observations
with _NAME_=L(THETA) (y value) and _NAME_=THETA
(x value) is written to the OUTEST= data set. The
_RHS_ and _ALPHA_ variables are not used (are set to
missing). The number of observations depends on the difficulty
of the optimization problems.
values is specified, then a set of
(x,y) point coordinates in two adjacent observations
with _NAME_=L(THETA) (y value) and _NAME_=THETA
(x value) is written to the OUTEST= data set. The
_RHS_ and _ALPHA_ variables are not used (are set to
missing). The number of observations depends on the difficulty
of the optimization problems.