Constructing Uniformly Weighted Moving Average Charts

MACHART Statement

Constructing Uniformly Weighted Moving Average Charts

The following notation is used in this section:

A_i uniformly weighted moving average for the i^th subgroup

w span parameter (number of terms in moving average)

$\mu$ process mean (expected value of the population of measurements)

$\sigma$ process standard deviation (standard deviation of the population of measurements)

x_ij j^th measurement in i^th subgroup, with j =1, 2, 3, ..., n_i

n_i sample size of i^th subgroup

$\overline{X}_{i}$ mean of measurements in i^th subgroup. If n_i=1, then the subgroup mean reduces to the single observation in the subgroup.

$\overline{\overline{X}}$ weighted average of subgroup means

$\Phi^{-1}(\cdot)$ inverse standard normal function

Plotted Points

Each point on the chart indicates the value of the uniformly weighted moving average for that subgroup. The moving average for the i^th subgroup (A_i) is defined as

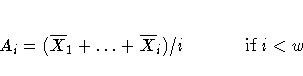
$A_{i}=(\overline{X}_{1}+ ... +\overline{X}_{i})/i \;\;\;\;\;\;\;\;\;\;\;\; {\rm if } \; i\lt w$

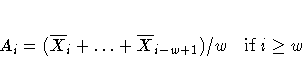
$A_{i}=(\overline{X}_{i}+ ... +\overline{X}_{i-w+1})/w \;\;\; {\rm if } \; i\geq w$

where w is the span, or number of terms, of the moving average. You can specify the span with the SPAN= option in the MACHART statement or with the value of _SPAN_ in a LIMITS= data set.

Central Line

By default, the central line on a moving average chart indicates an estimate for $\mu$ , which is computed as

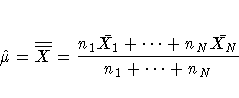
$\hat{\mu}=\overline{\overline{X}} = \frac{n_{1}\bar{X_{1}} + ... + n_{N}\bar{X_{N}}} {n_{1} + ... + n_{N}}$

If you specify a known value ( $\mu_{0}$ ) for $\mu$ ,the central line indicates the value of $\mu_{0}$ .

Control Limits

You can compute the limits in the following ways:

as a specified multiple (k) of the standard error of A_i above and below the central line. The default limits are computed with k=3 (these are referred to as $3\sigma$ limits).
as probability limits defined in terms of $\alpha$ , a specified probability that A_i exceeds the limits

The following table presents the formulas for the limits:

Table 21.19: Limits for Moving Average Chart

Control Limits

LCL = $\overline{\overline{X}}-k(\hat{\sigma}/\min(i,w)) \sqrt{ (1/n_{i}) + (1/n_{i-1}) + ... +(1/n_{1+\max(i-w,0)}) }$

UCL = $\overline{\overline{X}}+k(\hat{\sigma}/\min(i,w)) \sqrt{ (1/n_{i}) + (1/n_{i-1}) + ... +(1/n_{1+\max(i-w,0)}) }$

Probability Limits

LCL = $\overline{\overline{X}}-\Phi^{-1}(1-\alpha /2)(\hat{\sigma}/\min(i,w)) \sqrt{ (1/n_{i}) + (1/n_{i-1}) + ... +(1/n_{1+\max(i-w,0)}) }$

UCL = $\overline{\overline{X}}+\Phi^{-1}(1-\alpha /2)(\hat{\sigma}/\min(i,w)) \sqrt{ (1/n_{i}) + (1/n_{i-1}) + ... +(1/n_{1+\max(i-w,0)}) }$

These formulas assume that the data are normally distributed. If standard values $\mu_{0}$ and $\sigma_{0}$ are available for $\mu$ and $\sigma$ , respectively, replace $\overline{\overline{X}}$ with $\mu_{0}$ and replace $\hat{\sigma}$ with $\sigma_{0}$ in Table 21.19. Note that the limits vary with both n_i and i.

If the subgroup sample sizes are constant (n_i=n), the formulas for the control limits simplify to

${\rm LCL}&=&\overline{\overline{X}}-\frac{k\hat{\sigma}}{\sqrt{n\min(i,w) } } \ {\rm UCL}&=&\overline{\overline{X}}+\frac{k\hat{\sigma}}{\sqrt{n\min(i,w) } }$

Refer to Montgomery (1996) for more details. When the subgroup sample sizes are constant, the width of the control limits for the first w moving averages decreases monotonically because each of the first w moving averages includes one more term than the preceding moving average.

If you specify the ASYMPTOTIC option, constant control limits with the following values are displayed:

${\rm LCL}&=&\overline{\overline{X}}-\frac{k\hat{\sigma}}{\sqrt{nw} } \ {\rm UCL}&=&\overline{\overline{X}}+\frac{k\hat{\sigma}}{\sqrt{nw} }$

For asymptotic probability limits, replace k with $\Phi^{-1}(1-\alpha/2)$ in these equations. You can display asymptotic limits by specifying the ASYMPTOTIC option.

You can specify parameters for the moving average limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify a constant nominal sample size $n_{i} \equiv n$ for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify w with the SPAN= option or with the variable _SPAN_ in a LIMITS= data set.
Specify $\mu_{0}$ with the MU0= option or with the variable _MEAN_ in a LIMITS= data set.
Specify $\sigma_{0}$ with the SIGMA0= option or with the variable _STDDEV_ in a LIMITS= data set.

Choosing the Span of the Moving Average

There are few published guidelines for choosing the span w. In some applications, practical experience may dictate the choice of w. A more systematic approach is to choose w by considering its effect on the average run length (the expected number of points plotted before a shift is detected). This effect was studied by Roberts (1959), who used simulation methods.

You can use Table 21.20 and Table 21.21 to find a combination of k and w that yields a desired ARL for an in-control process ( $\delta=0$ ) and for a specified shift of $\delta$ .

Table 21.20: Average Run Lengths for One-Sided Uniformly Weighted Moving Average Charts

		w (span)
k	$\delta$	2	3	4	5	6	8	10

2.0	0.00	51.58	60.97	70.58	80.18	89.78	108.65	127.47
2.0	0.25	25.01	26.47	28.00	29.33	30.76	33.08	35.18
2.0	0.50	13.41	13.31	13.40	13.69	14.01	14.66	15.17
2.0	0.75	8.00	7.75	7.78	7.97	8.15	8.60	9.06
2.0	1.00	5.27	5.20	5.29	5.45	5.67	6.15	6.69
2.0	1.50	2.90	3.03	3.24	3.50	3.73	4.23	4.66
2.0	2.00	2.04	2.27	2.51	2.73	2.95	3.32	3.65
2.0	2.50	1.68	1.91	2.11	2.31	2.48	2.78	3.04
2.0	3.00	1.46	1.68	1.85	2.01	2.16	2.40	2.63
2.0	4.00	1.20	1.38	1.52	1.64	1.75	1.94	2.10
2.0	5.00	1.06	1.18	1.31	1.41	1.50	1.65	1.79

2.5	0.00	179.92	204.43	230.32	259.32	287.08	339.71	394.43
2.5	0.25	72.62	71.56	72.48	72.93	73.40	75.54	77.47
2.5	0.50	33.67	30.13	28.54	27.49	26.93	26.29	26.03
2.5	0.75	17.28	15.01	13.91	13.42	13.13	13.00	13.10
2.5	1.00	9.94	8.66	8.20	8.01	7.96	8.24	8.63
2.5	1.50	4.43	4.13	4.21	4.39	4.64	5.17	5.69
2.5	2.00	2.65	2.77	3.03	3.29	3.54	4.01	4.43
2.5	2.50	1.98	2.24	2.50	2.74	2.95	3.32	3.67
2.5	3.00	1.70	1.95	2.17	2.37	2.55	2.86	3.14
2.5	4.00	1.37	1.59	1.76	1.90	2.03	2.28	2.49
2.5	5.00	1.15	1.35	1.51	1.62	1.73	1.92	2.08

3.0	0.00	792.24	867.57	963.95	1051.77	1150.79	1345.96	1539.75
3.0	0.25	269.28	244.26	231.50	226.25	220.89	209.87	204.74
3.0	0.50	104.18	83.86	72.84	65.43	60.85	54.62	50.34
3.0	0.75	45.69	34.45	28.79	25.69	23.66	21.24	20.15
3.0	1.00	22.73	16.74	14.20	12.89	12.12	11.52	11.45
3.0	1.50	7.65	6.16	5.70	5.64	5.75	6.23	6.78
3.0	2.00	3.77	3.49	3.63	3.89	4.17	4.71	5.20
3.0	2.50	2.46	2.63	2.90	3.18	3.43	3.88	4.28
3.0	3.00	1.96	2.23	2.50	2.74	2.95	3.33	3.65
3.0	4.00	1.57	1.81	2.00	2.18	2.34	2.62	2.87
3.0	5.00	1.30	1.55	1.72	1.85	1.97	2.20	2.40

3.5	0.00	4275.15	4536.99	4853.63	5168.75	5485.97	6088.03	6613.01
3.5	0.25	1281.12	1078.59	964.86	886.26	830.03	751.66	684.98
3.5	0.50	413.30	294.47	235.00	197.27	169.50	136.01	115.48
3.5	0.75	153.50	98.31	73.49	59.29	50.49	40.45	34.53
3.5	1.00	63.68	39.34	29.37	24.06	20.88	17.70	16.12
3.5	1.50	15.84	10.44	8.50	7.78	7.47	7.51	7.97
3.5	2.00	6.06	4.73	4.49	4.61	4.86	5.43	6.01
3.5	2.50	3.27	3.13	3.34	3.63	3.92	4.45	4.91
3.5	3.00	2.31	2.54	2.83	3.11	3.36	3.80	4.19
3.5	4.00	1.77	2.02	2.25	2.45	2.64	2.97	3.27
3.5	5.00	1.48	1.74	1.91	2.06	2.21	2.48	2.71

Table 21.21: Average Run Lengths for Two-Sided Uniformly Weighted Moving Average Charts

w (span)

k $\delta$ 2 3 4 5 6 8 10

2.0 0.00 25.46 29.62 33.94 38.08 42.35 51.20 59.48

2.0 0.25 20.43 22.38 24.21 25.87 27.35 30.08 32.33

2.0 0.50 12.73 12.80 13.02 13.29 13.57 14.19 14.84

2.0 0.75 7.87 7.68 7.71 7.86 8.03 8.44 8.90

2.0 1.00 5.24 5.14 5.22 5.40 5.59 6.09 6.60

2.0 1.50 2.90 3.02 3.24 3.48 3.71 4.19 4.63

2.0 2.00 2.04 2.26 2.51 2.73 2.94 3.31 3.63

2.0 2.50 1.67 1.91 2.12 2.30 2.47 2.77 3.03

2.0 3.00 1.46 1.67 1.85 2.01 2.15 2.40 2.63

2.0 4.00 1.20 1.38 1.52 1.64 1.75 1.94 2.10

2.0 5.00 1.06 1.19 1.31 1.41 1.50 1.65 1.79

2.5 0.00 89.48 101.24 114.35 127.74 140.88 166.98 192.93

2.5 0.25 63.12 64.91 67.00 68.75 69.84 72.22 74.49

2.5 0.50 32.46 29.54 28.20 27.33 26.72 25.92 25.72

2.5 0.75 17.28 14.97 13.85 13.29 13.02 12.81 12.98

2.5 1.00 9.94 8.61 8.16 7.99 8.01 8.23 8.63

2.5 1.50 4.42 4.14 4.20 4.38 4.62 5.16 5.67

2.5 2.00 2.65 2.77 3.03 3.29 3.54 4.00 4.43

2.5 2.50 1.99 2.24 2.50 2.73 2.95 3.33 3.65

2.5 3.00 1.69 1.95 2.17 2.37 2.54 2.86 3.14

2.5 4.00 1.37 1.59 1.76 1.90 2.04 2.27 2.49

2.5 5.00 1.15 1.35 1.51 1.63 1.73 1.92 2.09

3.0 0.00 397.12 436.27 481.16 527.14 574.05 667.68 762.89

3.0 0.25 245.51 228.67 222.75 216.07 213.79 207.03 201.71

3.0 0.50 103.15 83.49 72.47 65.67 60.67 53.93 50.30

3.0 0.75 45.56 34.25 29.01 25.72 23.59 21.12 19.93

3.0 1.00 22.68 16.81 14.19 12.92 12.18 11.54 11.48

3.0 1.50 7.68 6.14 5.71 5.65 5.77 6.23 6.77

3.0 2.00 3.74 3.49 3.63 3.88 4.17 4.71 5.21

3.0 2.50 2.46 2.63 2.90 3.18 3.43 3.89 4.29

3.0 3.00 1.96 2.23 2.50 2.73 2.95 3.32 3.66

3.0 4.00 1.57 1.81 2.00 2.18 2.34 2.62 2.88

3.0 5.00 1.30 1.55 1.72 1.85 1.97 2.20 2.40

3.5 0.00 2217.61 2372.09 2567.27 2775.06 2983.70 3398.08 3810.50

3.5 0.25 1186.27 1027.67 940.30 875.91 826.53 744.59 676.61

3.5 0.50 411.69 295.62 232.68 195.65 169.21 135.73 116.06

3.5 0.75 152.52 97.33 72.30 58.98 50.59 40.22 34.71

3.5 1.00 64.03 39.46 29.18 24.08 20.80 17.54 16.16

3.5 1.50 15.83 10.36 8.47 7.73 7.46 7.56 8.00

3.5 2.00 6.05 4.71 4.49 4.61 4.85 5.44 6.00

3.5 2.50 3.27 3.12 3.34 3.64 3.92 4.44 4.91

3.5 3.00 2.32 2.54 2.83 3.11 3.36 3.80 4.19

3.5 4.00 1.77 2.02 2.25 2.46 2.65 2.97 3.26

3.5 5.00 1.49 1.74 1.91 2.06 2.21 2.48 2.71

For example, suppose you want to construct a two-sided moving average chart with an in-control ARL of 100 and an ARL of 9 for detecting a shift of $\delta=1$ . Table 21.21 shows that the combination w=3 and k=2.5 yields an in-control ARL of 101.24 and an ARL of 8.61 for $\delta=1$ .

Note that you can also use Table 21.20 and Table 21.21 to evaluate an existing moving average chart (see Example 21.2).

The following SAS program computes the average run length for a two-sided moving average chart for various shifts in the mean. This program can be adapted to compute averages run lengths for various combinations of k and w.

   data sim;
      drop span delta time j y x;
      span=4;
      do shift=0,.25,.5,.75,1,1.5,2,2.5,3,4,5;
         do j=1 to 50000;
            do time=1 to 15000;
               if time<=100 then
                  delta=0;
               else
                  delta=shift;
               y=delta+rannor(234);
               if time<span then
                  x=.;
               else
                  x=(y+lag1(y)+lag2(y)+lag3(y))/span;
               if time>=101 and abs(x)>3/sqrt(span)
                 then leave;
               end;
            arl=time-100;
            output;
            end;
         end;

   proc means;
      class shift;
   run;

In the preceding program, the size of the span w (SPAN) is 4 and the shifts in the mean are introduced to the variable (Y) $y\sim N(0,1)$ after the first 100 observations. The first DO loop specifies shifts of various magnitude, the second DO loop performs 50000 simulations for each shift, and the third DO loop counts the run length (TIME), that is, the number of samples observed before the control chart signals. A large upper bound (15000) for TIME is specified so that the run length is uncensored.

The program can be generalized for various span sizes by assigning a different value for the variable SPAN and changing the expression for X appropriately. Optionally, you can compute the ARL for a one-sided chart by changing the limits, that is, x>3/sqrt(span). This was the technique used to construct Table 21.20 and Table 21.21.

Chapter Contents
Previous
Next
Top

A_i	uniformly weighted moving average for the i^th subgroup
w	span parameter (number of terms in moving average)
$\mu$	process mean (expected value of the population of measurements)
$\sigma$	process standard deviation (standard deviation of the population of measurements)
x_ij	j^th measurement in i^th subgroup, with j =1, 2, 3, ..., n_i
n_i	sample size of i^th subgroup
$\overline{X}_{i}$	mean of measurements in i^th subgroup. If n_i=1, then the subgroup mean reduces to the single observation in the subgroup.
$\overline{\overline{X}}$	weighted average of subgroup means
$\Phi^{-1}(\cdot)$	inverse standard normal function