Example 32.6: Computing the Control Limits for Subgroup Maximums

BOXCHART Statement

Example 32.6: Computing the Control Limits for Subgroup Maximums

See SHWBOX3 in the SAS/QC Sample Library

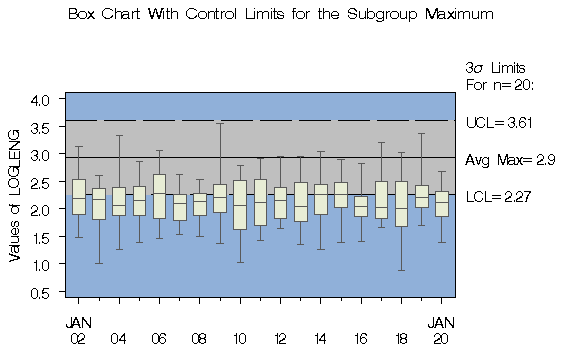
This example illustrates how to compute and display control limits for the maximum of a subgroup sample. Subgroup samples of 20 metal braces are collected daily, and the lengths of the braces are measured in centimeters. These data are analyzed extensively in Example 44.3. The box chart for LOGLENG (the log of length) shown in Output 44.3.3 indicates that the subgroup mean is in control and that the subgroup distributions of LOGLENG are approximately normal. The following statements save the control limits for the mean of the LOGLENG in a data set named LOGLLIMS:

   data lengdata;
      set lengdata;
      logleng=log(length-105);

   proc shewhart data=lengdata;
      xchart logleng*day /
         nochart
         outlimits=logllims;
   run;

The next statements replace the control limits for the mean of LOGLENG with control limits for the maximum of LOGLENG:

   data maxlim;
      set lengdata;
      set logllims;
      drop avgmax stdmax;
      label _lclx_ = 'Lower Limit for Maximum of 20'
            _uclx_ = 'Upper Limit for Maximum of 20'
            _mean_ = 'Central Line for Maximum of 20';
      avgmax = _stddev_*1.86747 + _mean_;
      stdmax = _stddev_*0.52509;
      _lclx_ = avgmax - _sigmas_*stdmax;
      _uclx_ = avgmax + _sigmas_*stdmax;
      _mean_ = avgmax;
      call symput('avgmax',left(put(avgmax,8.1)));
   run;

The control limits are computed using the fact that the maximum of a sample of size 20 from a normal population with zero mean and unit standard deviation has an expected value of 1.86747 and a standard deviation of 0.52509; refer to Teichroew (1956) and see Table 32.28. Finally, the following statements create a box chart for LOGLENG that displays control limits for the subgroup maximum:

   title 'Box Chart With Control Limits for the Subgroup Maximum';
   symbol v=none;

   proc shewhart data=lengdata limits=maxlim;
      boxchart logleng*day /
         cboxfill = ywh
         cinfill  = ligr
         serifs
         nohlabel
         nolegend
         xsymbol  = "Avg Max=&AVGMAX
         cboxes   = dagr
         cframe   = vligb;
      label logleng='Values of LOGLENG';
   run;

The box chart, shown in Output 32.6.1, indicates that the maximum is in control since the tips of the upper whiskers fall within the control limits.

The SYMPUT call is used to pass the value of _MEAN_ in a macro variable to the SHEWHART procedure so that this value can be used to label the central line.

You can apply the variable replacement method shown here to data with sample sizes other than 20 by replacing the constants 1.86747 and 0.52509 with the appropriate values from Table 32.28. Austin (1973) describes a method for approximating these values. You can also use the preceding statements to display control limits for the subgroup minimum by changing the sign of the expected values in Table 32.28.

Output 32.6.1: Box Chart for Subgroup Maximum

The variable replacement method can also be used to create a variety of box charts, including the modifications suggested by Iglewicz and Hoaglin (1987) and Rocke (1989).

Table 32.28: Expected Values and Standard Deviations of Maximum of a Normal Sample

n	Expected Value	Standard Deviation
2	0.56418	0.82565
3	0.84628	0.74798
4	1.02937	0.70123
5	1.16296	0.66899
6	1.26720	0.64494
7	1.35217	0.62605
8	1.42360	0.61065
9	1.48501	0.59780
10	1.53875	0.58681
11	1.58643	0.57730
12	1.62922	0.56891
13	1.66799	0.56144
14	1.70338	0.55474
15	1.73591	0.54869
16	1.76599	0.54316
17	1.79394	0.53809
18	1.82003	0.53342
19	1.84448	0.52910
20	1.86747	0.52509

Chapter Contents
Previous
Next
Top