| Introduction to Structural Equations with Latent Variables |
A Combined Measurement-Structural Model with
Reciprocal Influence and Correlated Residuals
To illustrate a more complex model, this example uses
some well-known data from Haller and Butterworth (1960).
Various models and analyses of these data are given
by Duncan, Haller, and Portes (1968), J reskog
and S
reskog
and S rbom (1988), and Loehlin (1987).
rbom (1988), and Loehlin (1987).
The study is concerned with the career
aspirations of high-school students and how
these aspirations are affected by close friends.
The data are collected from 442
seventeen-year-old boys in Michigan.
There are 329 boys in the sample who named
another boy in the sample as a best friend.
The observations to be analyzed consist of the data from
these 329 boys paired with the data from their best friends.
The method of data collection introduces two statistical problems.
First, restricting the analysis to boys whose best friends are
in the original sample causes the reduced sample to be biased.
Second, since the data from a given boy may appear in two
or more observations, the observations are not independent.
Therefore, any statistical conclusions
should be considered tentative.
It is difficult to accurately assess the effects of the
dependence of the observations on the analysis, but it could be
argued on intuitive grounds that since each observation has data
from two boys and since it seems likely that many of the boys
will appear in the data set at least twice, the effective sample
size may be as small as half of the reported 329 observations.
The correlation matrix is taken from
J reskog and S
reskog and S rbom (1988).
rbom (1988).
title 'Peer Influences on Aspiration: Haller & Butterworth (1960)';
data aspire(type=corr);
_type_='corr';
input _name_ $ riq rpa rses roa rea fiq fpa fses foa fea;
label riq='Respondent: Intelligence'
rpa='Respondent: Parental Aspiration'
rses='Respondent: Family SES'
roa='Respondent: Occupational Aspiration'
rea='Respondent: Educational Aspiration'
fiq='Friend: Intelligence'
fpa='Friend: Parental Aspiration'
fses='Friend: Family SES'
foa='Friend: Occupational Aspiration'
fea='Friend: Educational Aspiration';
datalines;
riq 1. . . . . . . . . .
rpa .1839 1. . . . . . . . .
rses .2220 .0489 1. . . . . . . .
roa .4105 .2137 .3240 1. . . . . . .
rea .4043 .2742 .4047 .6247 1. . . . . .
fiq .3355 .0782 .2302 .2995 .2863 1. . . . .
fpa .1021 .1147 .0931 .0760 .0702 .2087 1. . . .
fses .1861 .0186 .2707 .2930 .2407 .2950 -.0438 1. . .
foa .2598 .0839 .2786 .4216 .3275 .5007 .1988 .3607 1. .
fea .2903 .1124 .3054 .3269 .3669 .5191 .2784 .4105 .6404 1.
;
The model analyzed by J reskog and S
reskog and S rbom
(1988) is displayed in the following path diagram:
rbom
(1988) is displayed in the following path diagram:
Figure 14.17: Path Diagram: Career Aspiration, J reskog and S
reskog and S rbom
rbom
Two latent variables, f_ramb and f_famb,
represent the respondent's level of ambition and
his best friend's level of ambition, respectively.
The model states that the respondent's ambition is
determined by his intelligence and socioeconomic status,
his perception of his parents' aspiration for him,
and his friend's socioeconomic status and ambition.
It is assumed that his friend's intelligence and
socioeconomic status affect the respondent's ambition
only indirectly through his friend's ambition.
Ambition is indexed by the manifest variables of
occupational and educational aspiration, which
are assumed to have uncorrelated residuals.
The path coefficient from ambition to occupational aspiration is
set to 1.0 to determine the scale of the ambition latent variable.
This model can be analyzed with PROC CALIS using the LINEQS
statement as follows, where the names of the parameters
correspond to those used by J reskog and S
reskog and S rbom (1988).
Since this TYPE=CORR data set does not contain an
observation with _TYPE_='N' giving the sample size, it
is necessary to specify the degrees of freedom (sample size
minus one) with the EDF= option in the PROC CALIS statement.
rbom (1988).
Since this TYPE=CORR data set does not contain an
observation with _TYPE_='N' giving the sample size, it
is necessary to specify the degrees of freedom (sample size
minus one) with the EDF= option in the PROC CALIS statement.
title2 'Joreskog-Sorbom (1988) analysis 1';
proc calis data=aspire edf=328;
lineqs /* measurement model for aspiration */
rea=lambda2 f_ramb + e_rea,
roa=f_ramb + e_roa,
fea=lambda3 f_famb + e_fea,
foa=f_famb + e_foa,
/* structural model of influences */
f_ramb=gam1 rpa + gam2 riq + gam3 rses +
gam4 fses + beta1 f_famb + d_ramb,
f_famb=gam8 fpa + gam7 fiq + gam6 fses +
gam5 rses + beta2 f_ramb + d_famb;
std d_ramb=psi11,
d_famb=psi22,
e_rea e_roa e_fea e_foa=theta:;
cov d_ramb d_famb=psi12,
rpa riq rses fpa fiq fses=cov:;
run;
Specify a name followed by a colon to represent a list of
names formed by appending numbers to the specified name. For example,
in the COV statement, the line
rpa riq rses fpa fiq fses=cov:;
is equivalent to
rpa riq rses fpa fiq fses=cov1-cov15;
The results from this analysis are as follows.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Joreskog-Sorbom (1988) analysis 1 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0814 |
| Goodness of Fit Index (GFI) |
0.9844 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9428 |
| Root Mean Square Residual (RMR) |
0.0202 |
| Parsimonious GFI (Mulaik, 1989) |
0.3281 |
| Chi-Square |
26.6972 |
| Chi-Square DF |
15 |
| Pr > Chi-Square |
0.0313 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0488 |
| RMSEA 90% Lower Confidence Limit |
0.0145 |
| RMSEA 90% Upper Confidence Limit |
0.0783 |
| ECVI Estimate |
0.2959 |
| ECVI 90% Lower Confidence Limit |
0.2823 |
| ECVI 90% Upper Confidence Limit |
0.3721 |
| Probability of Close Fit |
0.4876 |
| Bentler's Comparative Fit Index |
0.9859 |
| Normal Theory Reweighted LS Chi-Square |
26.0113 |
| Akaike's Information Criterion |
-3.3028 |
| Bozdogan's (1987) CAIC |
-75.2437 |
| Schwarz's Bayesian Criterion |
-60.2437 |
| McDonald's (1989) Centrality |
0.9824 |
| Bentler & Bonett's (1980) Non-normed Index |
0.9576 |
| Bentler & Bonett's (1980) NFI |
0.9694 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.3231 |
| Z-Test of Wilson & Hilferty (1931) |
1.8625 |
| Bollen (1986) Normed Index Rho1 |
0.9082 |
| Bollen (1988) Non-normed Index Delta2 |
0.9864 |
| Hoelter's (1983) Critical N |
309 |
|
Figure 14.18: Career Aspiration Data: J&S Analysis 1
J reskog and S
reskog and S rbom (1988) present more detailed results
from a second analysis in which two constraints are imposed:
rbom (1988) present more detailed results
from a second analysis in which two constraints are imposed:
- The coefficents connecting the
latent ambition variables are equal.
- The covariance of the disturbances
of the ambition variables is zero.
This analysis can be performed
by changing the names beta1 and beta2
to beta and omitting the line from the COV statement for psi12:
title2 'Joreskog-Sorbom (1988) analysis 2';
proc calis data=aspire edf=328;
lineqs /* measurement model for aspiration */
rea=lambda2 f_ramb + e_rea,
roa=f_ramb + e_roa,
fea=lambda3 f_famb + e_fea,
foa=f_famb + e_foa,
/* structural model of influences */
f_ramb=gam1 rpa + gam2 riq + gam3 rses +
gam4 fses + beta f_famb + d_ramb,
f_famb=gam8 fpa + gam7 fiq + gam6 fses +
gam5 rses + beta f_ramb + d_famb;
std d_ramb=psi11,
d_famb=psi22,
e_rea e_roa e_fea e_foa=theta:;
cov rpa riq rses fpa fiq fses=cov:;
run;
The results are displayed in Figure 14.19.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Joreskog-Sorbom (1988) analysis 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0820 |
| Goodness of Fit Index (GFI) |
0.9843 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9492 |
| Root Mean Square Residual (RMR) |
0.0203 |
| Parsimonious GFI (Mulaik, 1989) |
0.3718 |
| Chi-Square |
26.8987 |
| Chi-Square DF |
17 |
| Pr > Chi-Square |
0.0596 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0421 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0710 |
| ECVI Estimate |
0.2839 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.3592 |
| Probability of Close Fit |
0.6367 |
| Bentler's Comparative Fit Index |
0.9880 |
| Normal Theory Reweighted LS Chi-Square |
26.1595 |
| Akaike's Information Criterion |
-7.1013 |
| Bozdogan's (1987) CAIC |
-88.6343 |
| Schwarz's Bayesian Criterion |
-71.6343 |
| McDonald's (1989) Centrality |
0.9851 |
| Bentler & Bonett's (1980) Non-normed Index |
0.9683 |
| Bentler & Bonett's (1980) NFI |
0.9692 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.3661 |
| Z-Test of Wilson & Hilferty (1931) |
1.5599 |
| Bollen (1986) Normed Index Rho1 |
0.9183 |
| Bollen (1988) Non-normed Index Delta2 |
0.9884 |
| Hoelter's (1983) Critical N |
338 |
|
Figure 14.19: Career Aspiration Data: J&S Analysis 2
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Joreskog-Sorbom (1988) analysis 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.0610 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0892 |
|
lambda2 |
|
|
|
|
| t Value |
|
11.8923 |
|
|
|
|
|
|
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.0736 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0806 |
|
lambda3 |
|
|
|
|
| t Value |
|
13.3150 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Joreskog-Sorbom (1988) analysis 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0.1801 |
* |
f_famb |
+ |
0.2540 |
* |
riq |
+ |
0.1637 |
* |
rpa |
+ |
0.2211 |
* |
rses |
+ |
0.0773 |
* |
fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
0.0391 |
|
beta |
|
0.0419 |
|
gam2 |
|
0.0387 |
|
gam1 |
|
0.0419 |
|
gam3 |
|
0.0415 |
|
gam4 |
|
|
|
|
| t Value |
|
4.6031 |
|
|
|
6.0673 |
|
|
|
4.2274 |
|
|
|
5.2822 |
|
|
|
1.8626 |
|
|
|
|
|
|
| f_famb |
= |
0.1801 |
* |
f_ramb |
+ |
0.0684 |
* |
rses |
+ |
0.3306 |
* |
fiq |
+ |
0.1520 |
* |
fpa |
+ |
0.2184 |
* |
fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
0.0391 |
|
beta |
|
0.0387 |
|
gam5 |
|
0.0412 |
|
gam7 |
|
0.0364 |
|
gam8 |
|
0.0395 |
|
gam6 |
|
|
|
|
| t Value |
|
4.6031 |
|
|
|
1.7681 |
|
|
|
8.0331 |
|
|
|
4.1817 |
|
|
|
5.5320 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Joreskog-Sorbom (1988) analysis 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| riq |
|
1.00000 |
|
|
| rpa |
|
1.00000 |
|
|
| rses |
|
1.00000 |
|
|
| fiq |
|
1.00000 |
|
|
| fpa |
|
1.00000 |
|
|
| fses |
|
1.00000 |
|
|
| e_rea |
theta1 |
0.33764 |
0.05178 |
6.52 |
| e_roa |
theta2 |
0.41205 |
0.05103 |
8.07 |
| e_fea |
theta3 |
0.31337 |
0.04574 |
6.85 |
| e_foa |
theta4 |
0.40381 |
0.04608 |
8.76 |
| d_ramb |
psi11 |
0.28113 |
0.04640 |
6.06 |
| d_famb |
psi22 |
0.22924 |
0.03889 |
5.89 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| riq |
rpa |
cov1 |
0.18390 |
0.05246 |
3.51 |
| riq |
rses |
cov3 |
0.22200 |
0.05110 |
4.34 |
| rpa |
rses |
cov2 |
0.04890 |
0.05493 |
0.89 |
| riq |
fiq |
cov8 |
0.33550 |
0.04641 |
7.23 |
| rpa |
fiq |
cov7 |
0.07820 |
0.05455 |
1.43 |
| rses |
fiq |
cov9 |
0.23020 |
0.05074 |
4.54 |
| riq |
fpa |
cov5 |
0.10210 |
0.05415 |
1.89 |
| rpa |
fpa |
cov4 |
0.11470 |
0.05412 |
2.12 |
| rses |
fpa |
cov6 |
0.09310 |
0.05438 |
1.71 |
| fiq |
fpa |
cov10 |
0.20870 |
0.05163 |
4.04 |
| riq |
fses |
cov12 |
0.18610 |
0.05209 |
3.57 |
| rpa |
fses |
cov11 |
0.01860 |
0.05510 |
0.34 |
| rses |
fses |
cov13 |
0.27070 |
0.04930 |
5.49 |
| fiq |
fses |
cov15 |
0.29500 |
0.04824 |
6.12 |
| fpa |
fses |
cov14 |
-0.04380 |
0.05476 |
-0.80 |
|
The difference between the chi-square values for the
two preceding models is 26.8987 - 26.6972= 0.2015 with 2
degrees of freedom, which is far from significant.
However, the chi-square test of the restricted model (analysis 2)
against the alternative of a completely unrestricted covariance
matrix yields a p-value of 0.0596, which indicates that the model
may not be entirely satisfactory (p-values from these data are
probably too small because of the dependence of the observations).
Loehlin (1987) points out that the models considered
are unrealistic in at least two aspects.
First, the variables of parental aspiration, intelligence, and
socioeconomic status are assumed to be measured without error.
Loehlin adds uncorrelated measurement errors to the model and
assumes, for illustrative purposes, that the reliabilities of
these variables are known to be 0.7, 0.8, and 0.9, respectively.
In practice, these reliabilities would need to be obtained
from a separate study of the same or a very similar population.
If these constraints are omitted, the model is not identified.
However, constraining parameters to a constant in
an analysis of a correlation matrix may make the
chi-square goodness-of-fit test inaccurate, so there
is more reason to be skeptical of the p-values.
Second, the error terms for the respondent's aspiration are assumed
to be uncorrelated with the corresponding terms for his friend.
Loehlin introduces a correlation between the two
educational aspiration error terms and between
the two occupational aspiration error terms.
These additions produce the following
path diagram for Loehlin's model 1.
Figure 14.20: Path Diagram: Carrer Aspiration -- Loehlin
The statements for fitting this model are as follows:
title2 'Loehlin (1987) analysis: Model 1';
proc calis data=aspire edf=328;
lineqs /* measurement model for aspiration */
rea=lambda2 f_ramb + e_rea,
roa=f_ramb + e_roa,
fea=lambda3 f_famb + e_fea,
foa=f_famb + e_foa,
/* measurement model for intelligence and environment */
rpa=.837 f_rpa + e_rpa,
riq=.894 f_riq + e_riq,
rses=.949 f_rses + e_rses,
fpa=.837 f_fpa + e_fpa,
fiq=.894 f_fiq + e_fiq,
fses=.949 f_fses + e_fses,
/* structural model of influences */
f_ramb=gam1 f_rpa + gam2 f_riq + gam3 f_rses +
gam4 f_fses + bet1 f_famb + d_ramb,
f_famb=gam8 f_fpa + gam7 f_fiq + gam6 f_fses +
gam5 f_rses + bet2 f_ramb + d_famb;
std d_ramb=psi11,
d_famb=psi22,
f_rpa f_riq f_rses f_fpa f_fiq f_fses=1,
e_rea e_roa e_fea e_foa=theta:,
e_rpa e_riq e_rses e_fpa e_fiq e_fses=err:;
cov d_ramb d_famb=psi12,
e_rea e_fea=covea,
e_roa e_foa=covoa,
f_rpa f_riq f_rses f_fpa f_fiq f_fses=cov:;
run;
The results are displayed in Figure 14.21.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 1 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0366 |
| Goodness of Fit Index (GFI) |
0.9927 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9692 |
| Root Mean Square Residual (RMR) |
0.0149 |
| Parsimonious GFI (Mulaik, 1989) |
0.2868 |
| Chi-Square |
12.0132 |
| Chi-Square DF |
13 |
| Pr > Chi-Square |
0.5266 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0512 |
| ECVI Estimate |
0.3016 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.3392 |
| Probability of Close Fit |
0.9435 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
12.0168 |
| Akaike's Information Criterion |
-13.9868 |
| Bozdogan's (1987) CAIC |
-76.3356 |
| Schwarz's Bayesian Criterion |
-63.3356 |
| McDonald's (1989) Centrality |
1.0015 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0041 |
| Bentler & Bonett's (1980) NFI |
0.9862 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.2849 |
| Z-Test of Wilson & Hilferty (1931) |
-0.0679 |
| Bollen (1986) Normed Index Rho1 |
0.9523 |
| Bollen (1988) Non-normed Index Delta2 |
1.0011 |
| Hoelter's (1983) Critical N |
612 |
|
Figure 14.21: Career Aspiration Data: Loehlin Model 1
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 1 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| riq |
= |
0.8940 |
|
f_riq |
+ |
1.0000 |
|
e_riq |
| rpa |
= |
0.8370 |
|
f_rpa |
+ |
1.0000 |
|
e_rpa |
| rses |
= |
0.9490 |
|
f_rses |
+ |
1.0000 |
|
e_rses |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.0840 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0942 |
|
lambda2 |
|
|
|
|
| t Value |
|
11.5105 |
|
|
|
|
|
|
| fiq |
= |
0.8940 |
|
f_fiq |
+ |
1.0000 |
|
e_fiq |
| fpa |
= |
0.8370 |
|
f_fpa |
+ |
1.0000 |
|
e_fpa |
| fses |
= |
0.9490 |
|
f_fses |
+ |
1.0000 |
|
e_fses |
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.1163 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0863 |
|
lambda3 |
|
|
|
|
| t Value |
|
12.9394 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 1 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0.1190 |
* |
f_famb |
+ |
0.1837 |
* |
f_rpa |
+ |
0.2800 |
* |
f_riq |
+ |
0.2262 |
* |
f_rses |
+ |
0.0870 |
* |
f_fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
0.1140 |
|
bet1 |
|
0.0504 |
|
gam1 |
|
0.0614 |
|
gam2 |
|
0.0522 |
|
gam3 |
|
0.0548 |
|
gam4 |
|
|
|
|
| t Value |
|
1.0440 |
|
|
|
3.6420 |
|
|
|
4.5618 |
|
|
|
4.3300 |
|
|
|
1.5884 |
|
|
|
|
|
|
| f_famb |
= |
0.1302 |
* |
f_ramb |
+ |
0.0633 |
* |
f_rses |
+ |
0.1688 |
* |
f_fpa |
+ |
0.3539 |
* |
f_fiq |
+ |
0.2154 |
* |
f_fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
0.1207 |
|
bet2 |
|
0.0522 |
|
gam5 |
|
0.0493 |
|
gam8 |
|
0.0674 |
|
gam7 |
|
0.0512 |
|
gam6 |
|
|
|
|
| t Value |
|
1.0792 |
|
|
|
1.2124 |
|
|
|
3.4205 |
|
|
|
5.2497 |
|
|
|
4.2060 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 1 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
|
1.00000 |
|
|
| f_riq |
|
1.00000 |
|
|
| f_rses |
|
1.00000 |
|
|
| f_fpa |
|
1.00000 |
|
|
| f_fiq |
|
1.00000 |
|
|
| f_fses |
|
1.00000 |
|
|
| e_rea |
theta1 |
0.32707 |
0.05452 |
6.00 |
| e_roa |
theta2 |
0.42307 |
0.05243 |
8.07 |
| e_fea |
theta3 |
0.28715 |
0.04804 |
5.98 |
| e_foa |
theta4 |
0.42240 |
0.04730 |
8.93 |
| e_rpa |
err1 |
0.29584 |
0.07774 |
3.81 |
| e_riq |
err2 |
0.20874 |
0.07832 |
2.67 |
| e_rses |
err3 |
0.09887 |
0.07803 |
1.27 |
| e_fpa |
err4 |
0.29987 |
0.07807 |
3.84 |
| e_fiq |
err5 |
0.19988 |
0.07674 |
2.60 |
| e_fses |
err6 |
0.10324 |
0.07824 |
1.32 |
| d_ramb |
psi11 |
0.25418 |
0.04469 |
5.69 |
| d_famb |
psi22 |
0.19698 |
0.03814 |
5.17 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
f_riq |
cov1 |
0.24677 |
0.07519 |
3.28 |
| f_rpa |
f_rses |
cov2 |
0.06184 |
0.06945 |
0.89 |
| f_riq |
f_rses |
cov3 |
0.26351 |
0.06687 |
3.94 |
| f_rpa |
f_fpa |
cov4 |
0.15789 |
0.07873 |
2.01 |
| f_riq |
f_fpa |
cov5 |
0.13085 |
0.07418 |
1.76 |
| f_rses |
f_fpa |
cov6 |
0.11517 |
0.06978 |
1.65 |
| f_rpa |
f_fiq |
cov7 |
0.10853 |
0.07362 |
1.47 |
| f_riq |
f_fiq |
cov8 |
0.42476 |
0.07219 |
5.88 |
| f_rses |
f_fiq |
cov9 |
0.27250 |
0.06660 |
4.09 |
| f_fpa |
f_fiq |
cov10 |
0.27867 |
0.07530 |
3.70 |
| f_rpa |
f_fses |
cov11 |
0.02383 |
0.06952 |
0.34 |
| f_riq |
f_fses |
cov12 |
0.22135 |
0.06648 |
3.33 |
| f_rses |
f_fses |
cov13 |
0.30156 |
0.06359 |
4.74 |
| f_fpa |
f_fses |
cov14 |
-0.05623 |
0.06971 |
-0.81 |
| f_fiq |
f_fses |
cov15 |
0.34922 |
0.06771 |
5.16 |
| e_rea |
e_fea |
covea |
0.02308 |
0.03139 |
0.74 |
| e_roa |
e_foa |
covoa |
0.11206 |
0.03258 |
3.44 |
| d_ramb |
d_famb |
psi12 |
-0.00935 |
0.05010 |
-0.19 |
|
Since the p-value for the chi-square test is
0.5266, this model clearly cannot be rejected.
However, Schwarz's Bayesian Criterion for this model
(SBC = -63.3356) is somewhat larger than for J reskog
and S
reskog
and S rbom's (1988) analysis 2 (SBC =-71.6343),
suggesting that a more parsimonious model would be desirable.
rbom's (1988) analysis 2 (SBC =-71.6343),
suggesting that a more parsimonious model would be desirable.
Since it is assumed that the same model applies to all
the boys in the sample, the path diagram should be
symmetric with respect to the respondent and friend.
In particular, the corresponding coefficients should be equal.
By imposing equality constraints on the 15 pairs of
corresponding coefficents, this example obtains Loehlin's model 2.
The LINEQS model is as follows, where an OUTRAM= data
set is created to facilitate subsequent hypothesis tests:
title2 'Loehlin (1987) analysis: Model 2';
proc calis data=aspire edf=328 outram=ram2;
lineqs /* measurement model for aspiration */
rea=lambda f_ramb + e_rea, /* 1 ec! */
roa=f_ramb + e_roa,
fea=lambda f_famb + e_fea,
foa=f_famb + e_foa,
/* measurement model for intelligence and environment */
rpa=.837 f_rpa + e_rpa,
riq=.894 f_riq + e_riq,
rses=.949 f_rses + e_rses,
fpa=.837 f_fpa + e_fpa,
fiq=.894 f_fiq + e_fiq,
fses=.949 f_fses + e_fses,
/* structural model of influences */ /* 5 ec! */
f_ramb=gam1 f_rpa + gam2 f_riq + gam3 f_rses +
gam4 f_fses + beta f_famb + d_ramb,
f_famb=gam1 f_fpa + gam2 f_fiq + gam3 f_fses +
gam4 f_rses + beta f_ramb + d_famb;
std d_ramb=psi, /* 1 ec! */
d_famb=psi,
f_rpa f_riq f_rses f_fpa f_fiq f_fses=1,
e_rea e_fea=thetaea thetaea, /* 2 ec! */
e_roa e_foa=thetaoa thetaoa,
e_rpa e_fpa=errpa1 errpa2,
e_riq e_fiq=erriq1 erriq2,
e_rses e_fses=errses1 errses2;
cov d_ramb d_famb=psi12,
e_rea e_fea=covea,
e_roa e_foa = covoa,
f_rpa f_riq f_rses=cov1-cov3, /* 3 ec! */
f_fpa f_fiq f_fses=cov1-cov3,
f_rpa f_riq f_rses * f_fpa f_fiq f_fses = /* 3 ec! */
cov4 cov5 cov6
cov5 cov7 cov8
cov6 cov8 cov9;
run;
The results are displayed in Figure 14.22.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0581 |
| Goodness of Fit Index (GFI) |
0.9884 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9772 |
| Root Mean Square Residual (RMR) |
0.0276 |
| Parsimonious GFI (Mulaik, 1989) |
0.6150 |
| Chi-Square |
19.0697 |
| Chi-Square DF |
28 |
| Pr > Chi-Square |
0.8960 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0194 |
| ECVI Estimate |
0.2285 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.2664 |
| Probability of Close Fit |
0.9996 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
19.2372 |
| Akaike's Information Criterion |
-36.9303 |
| Bozdogan's (1987) CAIC |
-171.2200 |
| Schwarz's Bayesian Criterion |
-143.2200 |
| McDonald's (1989) Centrality |
1.0137 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0174 |
| Bentler & Bonett's (1980) NFI |
0.9781 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6086 |
| Z-Test of Wilson & Hilferty (1931) |
-1.2599 |
| Bollen (1986) Normed Index Rho1 |
0.9649 |
| Bollen (1988) Non-normed Index Delta2 |
1.0106 |
| Hoelter's (1983) Critical N |
713 |
|
Figure 14.22: Career Aspiration Data: Loehlin Model 2
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| riq |
= |
0.8940 |
|
f_riq |
+ |
1.0000 |
|
e_riq |
| rpa |
= |
0.8370 |
|
f_rpa |
+ |
1.0000 |
|
e_rpa |
| rses |
= |
0.9490 |
|
f_rses |
+ |
1.0000 |
|
e_rses |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.1007 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0684 |
|
lambda |
|
|
|
|
| t Value |
|
16.0879 |
|
|
|
|
|
|
| fiq |
= |
0.8940 |
|
f_fiq |
+ |
1.0000 |
|
e_fiq |
| fpa |
= |
0.8370 |
|
f_fpa |
+ |
1.0000 |
|
e_fpa |
| fses |
= |
0.9490 |
|
f_fses |
+ |
1.0000 |
|
e_fses |
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.1007 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0684 |
|
lambda |
|
|
|
|
| t Value |
|
16.0879 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0.1158 |
* |
f_famb |
+ |
0.1758 |
* |
f_rpa |
+ |
0.3223 |
* |
f_riq |
+ |
0.2227 |
* |
f_rses |
+ |
0.0756 |
* |
f_fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
0.0839 |
|
beta |
|
0.0351 |
|
gam1 |
|
0.0470 |
|
gam2 |
|
0.0363 |
|
gam3 |
|
0.0375 |
|
gam4 |
|
|
|
|
| t Value |
|
1.3801 |
|
|
|
5.0130 |
|
|
|
6.8557 |
|
|
|
6.1373 |
|
|
|
2.0170 |
|
|
|
|
|
|
| f_famb |
= |
0.1158 |
* |
f_ramb |
+ |
0.0756 |
* |
f_rses |
+ |
0.1758 |
* |
f_fpa |
+ |
0.3223 |
* |
f_fiq |
+ |
0.2227 |
* |
f_fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
0.0839 |
|
beta |
|
0.0375 |
|
gam4 |
|
0.0351 |
|
gam1 |
|
0.0470 |
|
gam2 |
|
0.0363 |
|
gam3 |
|
|
|
|
| t Value |
|
1.3801 |
|
|
|
2.0170 |
|
|
|
5.0130 |
|
|
|
6.8557 |
|
|
|
6.1373 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 2 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
|
1.00000 |
|
|
| f_riq |
|
1.00000 |
|
|
| f_rses |
|
1.00000 |
|
|
| f_fpa |
|
1.00000 |
|
|
| f_fiq |
|
1.00000 |
|
|
| f_fses |
|
1.00000 |
|
|
| e_rea |
thetaea |
0.30662 |
0.03726 |
8.23 |
| e_roa |
thetaoa |
0.42295 |
0.03651 |
11.58 |
| e_fea |
thetaea |
0.30662 |
0.03726 |
8.23 |
| e_foa |
thetaoa |
0.42295 |
0.03651 |
11.58 |
| e_rpa |
errpa1 |
0.30758 |
0.07511 |
4.09 |
| e_riq |
erriq1 |
0.26656 |
0.07389 |
3.61 |
| e_rses |
errses1 |
0.11467 |
0.07267 |
1.58 |
| e_fpa |
errpa2 |
0.28834 |
0.07369 |
3.91 |
| e_fiq |
erriq2 |
0.15573 |
0.06700 |
2.32 |
| e_fses |
errses2 |
0.08814 |
0.07089 |
1.24 |
| d_ramb |
psi |
0.22456 |
0.02971 |
7.56 |
| d_famb |
psi |
0.22456 |
0.02971 |
7.56 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
f_riq |
cov1 |
0.26470 |
0.05442 |
4.86 |
| f_rpa |
f_rses |
cov2 |
0.00176 |
0.04996 |
0.04 |
| f_riq |
f_rses |
cov3 |
0.31129 |
0.05057 |
6.16 |
| f_rpa |
f_fpa |
cov4 |
0.15784 |
0.07872 |
2.01 |
| f_riq |
f_fpa |
cov5 |
0.11837 |
0.05447 |
2.17 |
| f_rses |
f_fpa |
cov6 |
0.06910 |
0.04996 |
1.38 |
| f_rpa |
f_fiq |
cov5 |
0.11837 |
0.05447 |
2.17 |
| f_riq |
f_fiq |
cov7 |
0.43061 |
0.07258 |
5.93 |
| f_rses |
f_fiq |
cov8 |
0.24967 |
0.05060 |
4.93 |
| f_fpa |
f_fiq |
cov1 |
0.26470 |
0.05442 |
4.86 |
| f_rpa |
f_fses |
cov6 |
0.06910 |
0.04996 |
1.38 |
| f_riq |
f_fses |
cov8 |
0.24967 |
0.05060 |
4.93 |
| f_rses |
f_fses |
cov9 |
0.30190 |
0.06362 |
4.75 |
| f_fpa |
f_fses |
cov2 |
0.00176 |
0.04996 |
0.04 |
| f_fiq |
f_fses |
cov3 |
0.31129 |
0.05057 |
6.16 |
| e_rea |
e_fea |
covea |
0.02160 |
0.03144 |
0.69 |
| e_roa |
e_foa |
covoa |
0.11208 |
0.03257 |
3.44 |
| d_ramb |
d_famb |
psi12 |
-0.00344 |
0.04931 |
-0.07 |
|
The test of Loehlin's model 2 against model 1 yields
a chi-square of 19.0697 - 12.0132 = 7.0565 with 15
degrees of freedom, which is clearly not significant.
Schwarz's Bayesizn Criterion (SBC)
is also much lower for model 2 (-143.2200) than model 1 (-63.3356).
Hence, model 2 seems preferable on both
substantive and statistical grounds.
A question of substantive interest is whether the friend's
socioeconomic status (SES)
has a significant direct influence on a boy's ambition.
This can be addressed by omitting the paths from f_fses
to f_ramb and from f_rses to f_famb designated by
the parameter name gam4, yielding Loehlin's model 3:
title2 'Loehlin (1987) analysis: Model 3';
data ram3(type=ram);
set ram2;
if _name_='gam4' then
do;
_name_=' ';
_estim_=0;
end;
run;
proc calis data=aspire edf=328 inram=ram3;
run;
The output is displayed in Figure 14.23.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 3 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0702 |
| Goodness of Fit Index (GFI) |
0.9858 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9731 |
| Root Mean Square Residual (RMR) |
0.0304 |
| Parsimonious GFI (Mulaik, 1989) |
0.6353 |
| Chi-Square |
23.0365 |
| Chi-Square DF |
29 |
| Pr > Chi-Square |
0.7749 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0295 |
| ECVI Estimate |
0.2343 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.2780 |
| Probability of Close Fit |
0.9984 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
23.5027 |
| Akaike's Information Criterion |
-34.9635 |
| Bozdogan's (1987) CAIC |
-174.0492 |
| Schwarz's Bayesian Criterion |
-145.0492 |
| McDonald's (1989) Centrality |
1.0091 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0112 |
| Bentler & Bonett's (1980) NFI |
0.9736 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6274 |
| Z-Test of Wilson & Hilferty (1931) |
-0.7563 |
| Bollen (1986) Normed Index Rho1 |
0.9590 |
| Bollen (1988) Non-normed Index Delta2 |
1.0071 |
| Hoelter's (1983) Critical N |
607 |
|
Figure 14.23: Career Aspiration Data: Loehlin Model 3
The chi-square value for testing model 3 versus
model 2 is 23.0365 - 19.0697 = 3.9668 with 1
degree of freedom and a p-value of 0.0464.
Although the parameter is of marginal
significance, the estimate in model 2 (0.0756) is
small compared to the other coefficients, and SBC
indicates that model 3 is preferable to model 2.
Another important question is whether the
reciprocal influences between the respondent's
and friend's ambitions are needed in the model.
To test whether these paths are zero, set the
parameter beta for the paths linking f_ramb
and f_famb to zero to obtain Loehlin's model 4:
title2 'Loehlin (1987) analysis: Model 4';
data ram4(type=ram);
set ram2;
if _name_='beta' then
do;
_name_=' ';
_estim_=0;
end;
run;
proc calis data=aspire edf=328 inram=ram4;
run;
The output is displayed in Figure 14.24.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 4 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0640 |
| Goodness of Fit Index (GFI) |
0.9873 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9760 |
| Root Mean Square Residual (RMR) |
0.0304 |
| Parsimonious GFI (Mulaik, 1989) |
0.6363 |
| Chi-Square |
20.9981 |
| Chi-Square DF |
29 |
| Pr > Chi-Square |
0.8592 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0234 |
| ECVI Estimate |
0.2281 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.2685 |
| Probability of Close Fit |
0.9994 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
20.8040 |
| Akaike's Information Criterion |
-37.0019 |
| Bozdogan's (1987) CAIC |
-176.0876 |
| Schwarz's Bayesian Criterion |
-147.0876 |
| McDonald's (1989) Centrality |
1.0122 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0150 |
| Bentler & Bonett's (1980) NFI |
0.9759 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6289 |
| Z-Test of Wilson & Hilferty (1931) |
-1.0780 |
| Bollen (1986) Normed Index Rho1 |
0.9626 |
| Bollen (1988) Non-normed Index Delta2 |
1.0095 |
| Hoelter's (1983) Critical N |
666 |
|
Figure 14.24: Career Aspiration Data: Loehlin Model 4
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 4 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| riq |
= |
0.8940 |
|
f_riq |
+ |
1.0000 |
|
e_riq |
| rpa |
= |
0.8370 |
|
f_rpa |
+ |
1.0000 |
|
e_rpa |
| rses |
= |
0.9490 |
|
f_rses |
+ |
1.0000 |
|
e_rses |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.1051 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0680 |
|
lambda |
|
|
|
|
| t Value |
|
16.2416 |
|
|
|
|
|
|
| fiq |
= |
0.8940 |
|
f_fiq |
+ |
1.0000 |
|
e_fiq |
| fpa |
= |
0.8370 |
|
f_fpa |
+ |
1.0000 |
|
e_fpa |
| fses |
= |
0.9490 |
|
f_fses |
+ |
1.0000 |
|
e_fses |
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.1051 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0680 |
|
lambda |
|
|
|
|
| t Value |
|
16.2416 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 4 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0 |
|
f_famb |
+ |
0.1776 |
* |
f_rpa |
+ |
0.3486 |
* |
f_riq |
+ |
0.2383 |
* |
f_rses |
+ |
0.1081 |
* |
f_fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
|
|
|
|
0.0361 |
|
gam1 |
|
0.0463 |
|
gam2 |
|
0.0355 |
|
gam3 |
|
0.0299 |
|
gam4 |
|
|
|
|
| t Value |
|
|
|
|
|
4.9195 |
|
|
|
7.5362 |
|
|
|
6.7158 |
|
|
|
3.6134 |
|
|
|
|
|
|
| f_famb |
= |
0 |
|
f_ramb |
+ |
0.1081 |
* |
f_rses |
+ |
0.1776 |
* |
f_fpa |
+ |
0.3486 |
* |
f_fiq |
+ |
0.2383 |
* |
f_fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
|
|
|
|
0.0299 |
|
gam4 |
|
0.0361 |
|
gam1 |
|
0.0463 |
|
gam2 |
|
0.0355 |
|
gam3 |
|
|
|
|
| t Value |
|
|
|
|
|
3.6134 |
|
|
|
4.9195 |
|
|
|
7.5362 |
|
|
|
6.7158 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 4 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
|
1.00000 |
|
|
| f_riq |
|
1.00000 |
|
|
| f_rses |
|
1.00000 |
|
|
| f_fpa |
|
1.00000 |
|
|
| f_fiq |
|
1.00000 |
|
|
| f_fses |
|
1.00000 |
|
|
| e_rea |
thetaea |
0.30502 |
0.03728 |
8.18 |
| e_roa |
thetaoa |
0.42429 |
0.03645 |
11.64 |
| e_fea |
thetaea |
0.30502 |
0.03728 |
8.18 |
| e_foa |
thetaoa |
0.42429 |
0.03645 |
11.64 |
| e_rpa |
errpa1 |
0.31354 |
0.07543 |
4.16 |
| e_riq |
erriq1 |
0.29611 |
0.07299 |
4.06 |
| e_rses |
errses1 |
0.12320 |
0.07273 |
1.69 |
| e_fpa |
errpa2 |
0.29051 |
0.07374 |
3.94 |
| e_fiq |
erriq2 |
0.18181 |
0.06611 |
2.75 |
| e_fses |
errses2 |
0.09873 |
0.07109 |
1.39 |
| d_ramb |
psi |
0.22738 |
0.03140 |
7.24 |
| d_famb |
psi |
0.22738 |
0.03140 |
7.24 |
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 4 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
f_riq |
cov1 |
0.27241 |
0.05520 |
4.94 |
| f_rpa |
f_rses |
cov2 |
0.00476 |
0.05032 |
0.09 |
| f_riq |
f_rses |
cov3 |
0.32463 |
0.05089 |
6.38 |
| f_rpa |
f_fpa |
cov4 |
0.16949 |
0.07863 |
2.16 |
| f_riq |
f_fpa |
cov5 |
0.13539 |
0.05407 |
2.50 |
| f_rses |
f_fpa |
cov6 |
0.07362 |
0.05027 |
1.46 |
| f_rpa |
f_fiq |
cov5 |
0.13539 |
0.05407 |
2.50 |
| f_riq |
f_fiq |
cov7 |
0.46893 |
0.06980 |
6.72 |
| f_rses |
f_fiq |
cov8 |
0.26289 |
0.05093 |
5.16 |
| f_fpa |
f_fiq |
cov1 |
0.27241 |
0.05520 |
4.94 |
| f_rpa |
f_fses |
cov6 |
0.07362 |
0.05027 |
1.46 |
| f_riq |
f_fses |
cov8 |
0.26289 |
0.05093 |
5.16 |
| f_rses |
f_fses |
cov9 |
0.30880 |
0.06409 |
4.82 |
| f_fpa |
f_fses |
cov2 |
0.00476 |
0.05032 |
0.09 |
| f_fiq |
f_fses |
cov3 |
0.32463 |
0.05089 |
6.38 |
| e_rea |
e_fea |
covea |
0.02127 |
0.03150 |
0.68 |
| e_roa |
e_foa |
covoa |
0.11245 |
0.03258 |
3.45 |
| d_ramb |
d_famb |
psi12 |
0.05479 |
0.02699 |
2.03 |
|
The chi-square value for testing model 4 versus
model 2 is 20.9981 - 19.0697 = 1.9284 with 1
degree of freedom and a p-value of 0.1649.
Hence, there is little evidence of reciprocal influence.
Loehlin's model 2 has not only the direct paths connecting
the latent ambition variables f_ramb and f_famb but also
a covariance between the disturbance terms d_ramb and
d_famb to allow for other variables omitted from the model
that might jointly influence the respondent and his friend.
To test the hypothesis that this covariance is zero, set
the parameter psi12 to zero, yielding Loehlin's model 5:
title2 'Loehlin (1987) analysis: Model 5';
data ram5(type=ram);
set ram2;
if _name_='psi12' then
do;
_name_=' ';
_estim_=0;
end;
run;
proc calis data=aspire edf=328 inram=ram5;
run;
The output is displayed in Figure 14.25.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 5 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0582 |
| Goodness of Fit Index (GFI) |
0.9884 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9780 |
| Root Mean Square Residual (RMR) |
0.0276 |
| Parsimonious GFI (Mulaik, 1989) |
0.6370 |
| Chi-Square |
19.0745 |
| Chi-Square DF |
29 |
| Pr > Chi-Square |
0.9194 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0152 |
| ECVI Estimate |
0.2222 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.2592 |
| Probability of Close Fit |
0.9998 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
19.2269 |
| Akaike's Information Criterion |
-38.9255 |
| Bozdogan's (1987) CAIC |
-178.0111 |
| Schwarz's Bayesian Criterion |
-149.0111 |
| McDonald's (1989) Centrality |
1.0152 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0186 |
| Bentler & Bonett's (1980) NFI |
0.9781 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6303 |
| Z-Test of Wilson & Hilferty (1931) |
-1.4014 |
| Bollen (1986) Normed Index Rho1 |
0.9661 |
| Bollen (1988) Non-normed Index Delta2 |
1.0118 |
| Hoelter's (1983) Critical N |
733 |
|
Figure 14.25: Career Aspiration Data: Loehlin Model 5
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 5 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| riq |
= |
0.8940 |
|
f_riq |
+ |
1.0000 |
|
e_riq |
| rpa |
= |
0.8370 |
|
f_rpa |
+ |
1.0000 |
|
e_rpa |
| rses |
= |
0.9490 |
|
f_rses |
+ |
1.0000 |
|
e_rses |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.1009 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0684 |
|
lambda |
|
|
|
|
| t Value |
|
16.1041 |
|
|
|
|
|
|
| fiq |
= |
0.8940 |
|
f_fiq |
+ |
1.0000 |
|
e_fiq |
| fpa |
= |
0.8370 |
|
f_fpa |
+ |
1.0000 |
|
e_fpa |
| fses |
= |
0.9490 |
|
f_fses |
+ |
1.0000 |
|
e_fses |
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.1009 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0684 |
|
lambda |
|
|
|
|
| t Value |
|
16.1041 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 5 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0.1107 |
* |
f_famb |
+ |
0.1762 |
* |
f_rpa |
+ |
0.3235 |
* |
f_riq |
+ |
0.2233 |
* |
f_rses |
+ |
0.0770 |
* |
f_fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
0.0428 |
|
beta |
|
0.0350 |
|
gam1 |
|
0.0435 |
|
gam2 |
|
0.0353 |
|
gam3 |
|
0.0323 |
|
gam4 |
|
|
|
|
| t Value |
|
2.5854 |
|
|
|
5.0308 |
|
|
|
7.4435 |
|
|
|
6.3215 |
|
|
|
2.3870 |
|
|
|
|
|
|
| f_famb |
= |
0.1107 |
* |
f_ramb |
+ |
0.0770 |
* |
f_rses |
+ |
0.1762 |
* |
f_fpa |
+ |
0.3235 |
* |
f_fiq |
+ |
0.2233 |
* |
f_fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
0.0428 |
|
beta |
|
0.0323 |
|
gam4 |
|
0.0350 |
|
gam1 |
|
0.0435 |
|
gam2 |
|
0.0353 |
|
gam3 |
|
|
|
|
| t Value |
|
2.5854 |
|
|
|
2.3870 |
|
|
|
5.0308 |
|
|
|
7.4435 |
|
|
|
6.3215 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 5 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
|
1.00000 |
|
|
| f_riq |
|
1.00000 |
|
|
| f_rses |
|
1.00000 |
|
|
| f_fpa |
|
1.00000 |
|
|
| f_fiq |
|
1.00000 |
|
|
| f_fses |
|
1.00000 |
|
|
| e_rea |
thetaea |
0.30645 |
0.03721 |
8.24 |
| e_roa |
thetaoa |
0.42304 |
0.03650 |
11.59 |
| e_fea |
thetaea |
0.30645 |
0.03721 |
8.24 |
| e_foa |
thetaoa |
0.42304 |
0.03650 |
11.59 |
| e_rpa |
errpa1 |
0.30781 |
0.07510 |
4.10 |
| e_riq |
erriq1 |
0.26748 |
0.07295 |
3.67 |
| e_rses |
errses1 |
0.11477 |
0.07265 |
1.58 |
| e_fpa |
errpa2 |
0.28837 |
0.07366 |
3.91 |
| e_fiq |
erriq2 |
0.15653 |
0.06614 |
2.37 |
| e_fses |
errses2 |
0.08832 |
0.07088 |
1.25 |
| d_ramb |
psi |
0.22453 |
0.02973 |
7.55 |
| d_famb |
psi |
0.22453 |
0.02973 |
7.55 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
f_riq |
cov1 |
0.26494 |
0.05436 |
4.87 |
| f_rpa |
f_rses |
cov2 |
0.00185 |
0.04995 |
0.04 |
| f_riq |
f_rses |
cov3 |
0.31164 |
0.05039 |
6.18 |
| f_rpa |
f_fpa |
cov4 |
0.15828 |
0.07846 |
2.02 |
| f_riq |
f_fpa |
cov5 |
0.11895 |
0.05383 |
2.21 |
| f_rses |
f_fpa |
cov6 |
0.06924 |
0.04993 |
1.39 |
| f_rpa |
f_fiq |
cov5 |
0.11895 |
0.05383 |
2.21 |
| f_riq |
f_fiq |
cov7 |
0.43180 |
0.07084 |
6.10 |
| f_rses |
f_fiq |
cov8 |
0.25004 |
0.05039 |
4.96 |
| f_fpa |
f_fiq |
cov1 |
0.26494 |
0.05436 |
4.87 |
| f_rpa |
f_fses |
cov6 |
0.06924 |
0.04993 |
1.39 |
| f_riq |
f_fses |
cov8 |
0.25004 |
0.05039 |
4.96 |
| f_rses |
f_fses |
cov9 |
0.30203 |
0.06360 |
4.75 |
| f_fpa |
f_fses |
cov2 |
0.00185 |
0.04995 |
0.04 |
| f_fiq |
f_fses |
cov3 |
0.31164 |
0.05039 |
6.18 |
| e_rea |
e_fea |
covea |
0.02120 |
0.03094 |
0.69 |
| e_roa |
e_foa |
covoa |
0.11197 |
0.03254 |
3.44 |
| d_ramb |
d_famb |
|
0 |
|
|
|
The chi-square value for testing model 5 versus model 2
is 19.0745 - 19.0697 = 0.0048 with 1 degree of freedom.
Omitting the covariance between the disturbance terms, therefore,
causes hardly any deterioration in the fit of the model.
These data fail to provide evidence of direct reciprocal
influence between the respondent's and friend's ambitions
or of a covariance between the disturbance terms
when these hypotheses are considered separately.
Notice, however, that the covariance psi12
between the disturbance terms increases from
-0.003344 for model 2 to 0.05479 for model 4.
Before you conclude that all of these paths can be omitted from
the model, it is important to test both hypotheses together by
setting both beta and psi12 to zero as in Loehlin's model 7:
title2 'Loehlin (1987) analysis: Model 7';
data ram7(type=ram);
set ram2;
if _name_='psi12'|_name_='beta' then
do;
_name_=' ';
_estim_=0;
end;
run;
proc calis data=aspire edf=328 inram=ram7;
run;
The relevant output is displayed in Figure 14.26.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 7 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.0773 |
| Goodness of Fit Index (GFI) |
0.9846 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9718 |
| Root Mean Square Residual (RMR) |
0.0363 |
| Parsimonious GFI (Mulaik, 1989) |
0.6564 |
| Chi-Square |
25.3466 |
| Chi-Square DF |
30 |
| Pr > Chi-Square |
0.7080 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0000 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0326 |
| ECVI Estimate |
0.2350 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.2815 |
| Probability of Close Fit |
0.9975 |
| Bentler's Comparative Fit Index |
1.0000 |
| Normal Theory Reweighted LS Chi-Square |
25.1291 |
| Akaike's Information Criterion |
-34.6534 |
| Bozdogan's (1987) CAIC |
-178.5351 |
| Schwarz's Bayesian Criterion |
-148.5351 |
| McDonald's (1989) Centrality |
1.0071 |
| Bentler & Bonett's (1980) Non-normed Index |
1.0084 |
| Bentler & Bonett's (1980) NFI |
0.9709 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6473 |
| Z-Test of Wilson & Hilferty (1931) |
-0.5487 |
| Bollen (1986) Normed Index Rho1 |
0.9564 |
| Bollen (1988) Non-normed Index Delta2 |
1.0055 |
| Hoelter's (1983) Critical N |
568 |
|
Figure 14.26: Career Aspiration Data: Loehlin Model 7
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 7 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| riq |
= |
0.8940 |
|
f_riq |
+ |
1.0000 |
|
e_riq |
| rpa |
= |
0.8370 |
|
f_rpa |
+ |
1.0000 |
|
e_rpa |
| rses |
= |
0.9490 |
|
f_rses |
+ |
1.0000 |
|
e_rses |
| roa |
= |
1.0000 |
|
f_ramb |
+ |
1.0000 |
|
e_roa |
| rea |
= |
1.1037 |
* |
f_ramb |
+ |
1.0000 |
|
e_rea |
| Std Err |
|
0.0678 |
|
lambda |
|
|
|
|
| t Value |
|
16.2701 |
|
|
|
|
|
|
| fiq |
= |
0.8940 |
|
f_fiq |
+ |
1.0000 |
|
e_fiq |
| fpa |
= |
0.8370 |
|
f_fpa |
+ |
1.0000 |
|
e_fpa |
| fses |
= |
0.9490 |
|
f_fses |
+ |
1.0000 |
|
e_fses |
| foa |
= |
1.0000 |
|
f_famb |
+ |
1.0000 |
|
e_foa |
| fea |
= |
1.1037 |
* |
f_famb |
+ |
1.0000 |
|
e_fea |
| Std Err |
|
0.0678 |
|
lambda |
|
|
|
|
| t Value |
|
16.2701 |
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 7 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| f_ramb |
= |
0 |
|
f_famb |
+ |
0.1765 |
* |
f_rpa |
+ |
0.3573 |
* |
f_riq |
+ |
0.2419 |
* |
f_rses |
+ |
0.1109 |
* |
f_fses |
+ |
1.0000 |
|
d_ramb |
| Std Err |
|
|
|
|
|
0.0360 |
|
gam1 |
|
0.0461 |
|
gam2 |
|
0.0363 |
|
gam3 |
|
0.0306 |
|
gam4 |
|
|
|
|
| t Value |
|
|
|
|
|
4.8981 |
|
|
|
7.7520 |
|
|
|
6.6671 |
|
|
|
3.6280 |
|
|
|
|
|
|
| f_famb |
= |
0 |
|
f_ramb |
+ |
0.1109 |
* |
f_rses |
+ |
0.1765 |
* |
f_fpa |
+ |
0.3573 |
* |
f_fiq |
+ |
0.2419 |
* |
f_fses |
+ |
1.0000 |
|
d_famb |
| Std Err |
|
|
|
|
|
0.0306 |
|
gam4 |
|
0.0360 |
|
gam1 |
|
0.0461 |
|
gam2 |
|
0.0363 |
|
gam3 |
|
|
|
|
| t Value |
|
|
|
|
|
3.6280 |
|
|
|
4.8981 |
|
|
|
7.7520 |
|
|
|
6.6671 |
|
|
|
|
|
|
|
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 7 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Variances of Exogenous Variables |
| Variable |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
|
1.00000 |
|
|
| f_riq |
|
1.00000 |
|
|
| f_rses |
|
1.00000 |
|
|
| f_fpa |
|
1.00000 |
|
|
| f_fiq |
|
1.00000 |
|
|
| f_fses |
|
1.00000 |
|
|
| e_rea |
thetaea |
0.31633 |
0.03648 |
8.67 |
| e_roa |
thetaoa |
0.42656 |
0.03610 |
11.82 |
| e_fea |
thetaea |
0.31633 |
0.03648 |
8.67 |
| e_foa |
thetaoa |
0.42656 |
0.03610 |
11.82 |
| e_rpa |
errpa1 |
0.31329 |
0.07538 |
4.16 |
| e_riq |
erriq1 |
0.30776 |
0.07307 |
4.21 |
| e_rses |
errses1 |
0.14303 |
0.07313 |
1.96 |
| e_fpa |
errpa2 |
0.29286 |
0.07389 |
3.96 |
| e_fiq |
erriq2 |
0.19193 |
0.06613 |
2.90 |
| e_fses |
errses2 |
0.11804 |
0.07147 |
1.65 |
| d_ramb |
psi |
0.21011 |
0.02940 |
7.15 |
| d_famb |
psi |
0.21011 |
0.02940 |
7.15 |
| Covariances Among Exogenous Variables |
| Var1 |
Var2 |
Parameter |
Estimate |
Standard
Error |
t Value |
| f_rpa |
f_riq |
cov1 |
0.27533 |
0.05552 |
4.96 |
| f_rpa |
f_rses |
cov2 |
0.00611 |
0.05085 |
0.12 |
| f_riq |
f_rses |
cov3 |
0.33510 |
0.05150 |
6.51 |
| f_rpa |
f_fpa |
cov4 |
0.17099 |
0.07872 |
2.17 |
| f_riq |
f_fpa |
cov5 |
0.13859 |
0.05431 |
2.55 |
| f_rses |
f_fpa |
cov6 |
0.07563 |
0.05077 |
1.49 |
| f_rpa |
f_fiq |
cov5 |
0.13859 |
0.05431 |
2.55 |
| f_riq |
f_fiq |
cov7 |
0.48105 |
0.06993 |
6.88 |
| f_rses |
f_fiq |
cov8 |
0.27235 |
0.05157 |
5.28 |
| f_fpa |
f_fiq |
cov1 |
0.27533 |
0.05552 |
4.96 |
| f_rpa |
f_fses |
cov6 |
0.07563 |
0.05077 |
1.49 |
| f_riq |
f_fses |
cov8 |
0.27235 |
0.05157 |
5.28 |
| f_rses |
f_fses |
cov9 |
0.32046 |
0.06517 |
4.92 |
| f_fpa |
f_fses |
cov2 |
0.00611 |
0.05085 |
0.12 |
| f_fiq |
f_fses |
cov3 |
0.33510 |
0.05150 |
6.51 |
| e_rea |
e_fea |
covea |
0.04535 |
0.02918 |
1.55 |
| e_roa |
e_foa |
covoa |
0.12085 |
0.03214 |
3.76 |
| d_ramb |
d_famb |
|
0 |
|
|
|
When model 7 is tested against models 2, 4, and 5, the p-values
are respectively 0.0433, 0.0370, and 0.0123, indicating that the
combined effect of the reciprocal influence and the covariance
of the disturbance terms is statistically significant.
Thus, the hypothesis tests indicate that it is
acceptable to omit either the reciprocal influences
or the covariance of the disturbances but not both.
It is also of interest to test the covariances between the error
terms for educational (COVEA) and occupational aspiration (COVOA),
since these
terms are omitted from J reskog and S
reskog and S rbom's models.
Constraining COVEA and COVOA to zero produces Loehlin's model 6:
rbom's models.
Constraining COVEA and COVOA to zero produces Loehlin's model 6:
title2 'Loehlin (1987) analysis: Model 6';
data ram6(type=ram);
set ram2;
if _name_='covea'|_name_='covoa' then
do;
_name_=' ';
_estim_=0;
end;
run;
proc calis data=aspire edf=328 inram=ram6;
run;
The relevant output is displayed in Figure 14.27.
|
| Peer Influences on Aspiration: Haller & Butterworth (1960) |
| Loehlin (1987) analysis: Model 6 |
| The CALIS Procedure |
| Covariance Structure Analysis: Maximum Likelihood Estimation |
| Fit Function |
0.1020 |
| Goodness of Fit Index (GFI) |
0.9802 |
| GFI Adjusted for Degrees of Freedom (AGFI) |
0.9638 |
| Root Mean Square Residual (RMR) |
0.0306 |
| Parsimonious GFI (Mulaik, 1989) |
0.6535 |
| Chi-Square |
33.4475 |
| Chi-Square DF |
30 |
| Pr > Chi-Square |
0.3035 |
| Independence Model Chi-Square |
872.00 |
| Independence Model Chi-Square DF |
45 |
| RMSEA Estimate |
0.0187 |
| RMSEA 90% Lower Confidence Limit |
. |
| RMSEA 90% Upper Confidence Limit |
0.0471 |
| ECVI Estimate |
0.2597 |
| ECVI 90% Lower Confidence Limit |
. |
| ECVI 90% Upper Confidence Limit |
0.3164 |
| Probability of Close Fit |
0.9686 |
| Bentler's Comparative Fit Index |
0.9958 |
| Normal Theory Reweighted LS Chi-Square |
32.9974 |
| Akaike's Information Criterion |
-26.5525 |
| Bozdogan's (1987) CAIC |
-170.4342 |
| Schwarz's Bayesian Criterion |
-140.4342 |
| McDonald's (1989) Centrality |
0.9948 |
| Bentler & Bonett's (1980) Non-normed Index |
0.9937 |
| Bentler & Bonett's (1980) NFI |
0.9616 |
| James, Mulaik, & Brett (1982) Parsimonious NFI |
0.6411 |
| Z-Test of Wilson & Hilferty (1931) |
0.5151 |
| Bollen (1986) Normed Index Rho1 |
0.9425 |
| Bollen (1988) Non-normed Index Delta2 |
0.9959 |
| Hoelter's (1983) Critical N |
431 |
|
Figure 14.27: Career Aspiration Data: Loehlin Model 6
The chi-square value for testing model 6 versus model 2 is
33.4476 - 19.0697 = 14.3779 with 2 degrees of freedom and a
p-value of 0.0008, indicating that there is considerable
evidence of correlation between the error terms.
The following table summarizes the
results from Loehlin's seven models.
|
Model
|
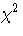
|
df
|
p-value
|
SBC
|
| 1. Full model | 12.0132 | 13 | 0.5266 | -63.3356 |
| 2. Equality constraints | 19.0697 | 28 | 0.8960 | -143.2200 |
| 3. No SES path | 23.0365 | 29 | 0.7749 | -145.0492 |
| 4. No reciprocal influence | 20.9981 | 29 | 0.8592 | -147.0876 |
| 5. No disturbance correlation | 19.0745 | 29 | 0.9194 | -149.0111 |
| 6. No error correlation | 33.4475 | 30 | 0.3035 | -140.4342 |
| 7. Constraints from both 4 & 5 | 25.3466 | 30 | 0.7080 | -148.5351 |
For comparing models, you can use a DATA step to compute the
differences of the chi-square statistics and p-values.
title 'Comparisons among Loehlin''s models';
data _null_;
array achisq[7] _temporary_
(12.0132 19.0697 23.0365 20.9981 19.0745 33.4475 25.3466);
array adf[7] _temporary_
(13 28 29 29 29 30 30);
retain indent 16;
file print;
input ho ha @@;
chisq = achisq[ho] - achisq[ha];
df = adf[ho] - adf[ha];
p = 1 - probchi( chisq, df);
if _n_ = 1 then put
/ +indent 'model comparison chi**2 df p-value'
/ +indent '---------------------------------------';
put +indent +3 ho ' versus ' ha @18 +indent chisq 8.4 df 5. p 9.4;
datalines;
2 1 3 2 4 2 5 2 7 2 7 4 7 5 6 2
;
The DATA step displays the following table.
Comparisons among Loehlin's models
model comparison chi**2 df p-value
---------------------------------------
2 versus 1 7.0565 15 0.9561
3 versus 2 3.9668 1 0.0464
4 versus 2 1.9284 1 0.1649
5 versus 2 0.0048 1 0.9448
7 versus 2 6.2769 2 0.0433
7 versus 4 4.3485 1 0.0370
7 versus 5 6.2721 1 0.0123
6 versus 2 14.3778 2 0.0008
Although none of the seven models can be rejected
when tested against the alternative of an unrestricted
covariance matrix, the model comparisons make it clear
that there are important differences among the models.
Schwarz's Bayesian Criterion indicates model 5 as the model of choice.
The constraints added to model 5 in model 7 can be rejected
(p=0.0123), while model 5 cannot be rejected when
tested against the less-constrained model 2 (p=0.9448).
Hence, among the small number of models considered,
model 5 has strong statistical support.
However, as Loehlin (1987, p. 106) points out, many
other models for these data could be constructed.
Further analysis should consider, in addition to
simple modifications of the models,
the possibility that more than one
friend could influence a boy's aspirations, and that a boy's
ambition might have some effect on his choice of friends.
Pursuing such theories would be statistically challenging.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![]() reskog
and S
reskog
and S![]() rbom (1988), and Loehlin (1987).
rbom (1988), and Loehlin (1987).
![]() reskog and S
reskog and S![]() rbom (1988).
rbom (1988).
![]() reskog and S
reskog and S![]() rbom
(1988) is displayed in the following path diagram:
rbom
(1988) is displayed in the following path diagram:
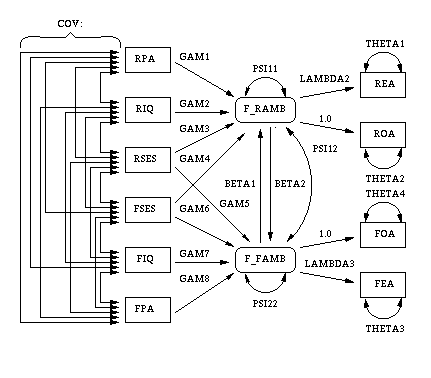
![]() reskog and S
reskog and S![]() rbom (1988).
Since this TYPE=CORR data set does not contain an
observation with _TYPE_='N' giving the sample size, it
is necessary to specify the degrees of freedom (sample size
minus one) with the EDF= option in the PROC CALIS statement.
rbom (1988).
Since this TYPE=CORR data set does not contain an
observation with _TYPE_='N' giving the sample size, it
is necessary to specify the degrees of freedom (sample size
minus one) with the EDF= option in the PROC CALIS statement.
![]() reskog and S
reskog and S![]() rbom (1988) present more detailed results
from a second analysis in which two constraints are imposed:
rbom (1988) present more detailed results
from a second analysis in which two constraints are imposed:
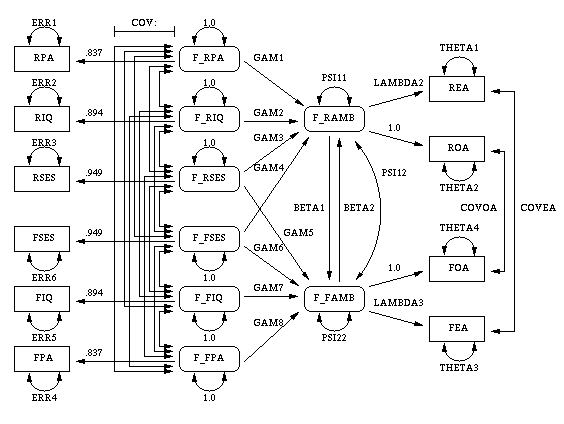
![]() reskog and S
reskog and S![]() rbom's models.
Constraining COVEA and COVOA to zero produces Loehlin's model 6:
rbom's models.
Constraining COVEA and COVOA to zero produces Loehlin's model 6: