Generalized Logits Model

The CATMOD Procedure

Generalized Logits Model

Over the course of one school year, third graders from three different schools are exposed to three different styles of mathematics instruction: a self-paced computer-learning style, a team approach, and a traditional class approach. The students are asked which style they prefer and their responses, classified by the type of program they are in (a regular school day versus a regular day supplemented with an afternoon school program) are displayed in Table 22.3. The data set is from Stokes, Davis, and Koch (1995).

Table 22.3: School Program Data

		Learning Style Preference
School	Program	Self	Team	Class
1	Regular	10	17	26
1	Afternoon	5	12	50
2	Regular	21	17	26
2	Afternoon	16	12	36
3	Regular	15	15	16
3	Afternoon	12	12	20

The levels of the response variable (self, team, and class) have no essential ordering, hence a logistic regression is performed on the generalized logits. The model to be fit is

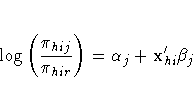
$\log(\frac{\pi_{hij}}{\pi_{hir}}) = \alpha_j + x_{hi}'\mathbf{\beta}_j$

where $\pi_{hij}$ is the probability that a student in school h and program i prefers teaching style j, $j\ne r$ , and style r is the class style. There are separate sets of intercept parameters $\alpha_j$ and regression parameters $\beta_j$ for each logit, and the matrix x_hi is the set of explanatory variables for the hith population. Thus, two logits are modeled for each school and program combination (population): the logit comparing self to class and the logit comparing team to class.

The following statements create the data set school and request the analysis. Generalized logits are the default response functions, and maximum likelihood estimation is the default method for analyzing generalized logits, so only the WEIGHT and MODEL statements are required. The option ORDER=DATA means that the response variable levels are ordered as they exist in the data set: self, team, and class; thus the logits are formed by comparing self to class and by comparing team to class. The results of this analysis are shown in Figure 22.8 and Figure 22.9.

   data school;
      length Program $ 9;
      input School Program $ Style $ Count @@; 
      datalines; 
   1 regular   self 10  1 regular   team 17  1 regular   class 26
   1 afternoon self  5  1 afternoon team 12  1 afternoon class 50 
   2 regular   self 21  2 regular   team 17  2 regular   class 26
   2 afternoon self 16  2 afternoon team 12  2 afternoon class 36 
   3 regular   self 15  3 regular   team 15  3 regular   class 16
   3 afternoon self 12  3 afternoon team 12  3 afternoon class 20 
   ; 
   proc catmod order=data;
      weight Count;
      model Style=School Program School*Program;
   run;

The CATMOD Procedure

Response	Style	Response Levels	3
Weight Variable	Count	Populations	6
Data Set	SCHOOL	Total Frequency	338
Frequency Missing	0	Observations	18

Population Profiles
Sample	School	Program	Sample Size
1	1	regular	53
2	1	afternoon	67
3	2	regular	64
4	2	afternoon	64
5	3	regular	46
6	3	afternoon	44

Response Profiles
Response	Style
1	self
2	team
3	class

Figure 22.8: Model Information and Profile Tables

A summary of the data set is displayed in Figure 22.8; the variable levels that form the three responses and six populations are listed in the "Response Profiles" and "Population Profiles" table, respectively. A table containing the iteration history is also produced, but it is not displayed here.

The CATMOD Procedure

Maximum Likelihood Analysis of Variance
Source	DF	Chi-Square	Pr > ChiSq
Intercept	2	40.05	<.0001
School	4	14.55	0.0057
Program	2	10.48	0.0053
*SchoolProgram**	4	1.74	0.7827
Likelihood Ratio	0	.	.

Figure 22.9: ANOVA Table

The analysis of variance table is displayed in Figure 22.9. Since this is a saturated model, there are no degrees of freedom remaining for a likelihood ratio test, and missing values are displayed in the table. The interaction effect is clearly nonsignificant, so a main effects model is fit.

Since PROC CATMOD is an interactive procedure, you can analyze the main effects model by simply submitting the new MODEL statement as follows.

   model Style=School Program;
   run;

The CATMOD Procedure

Maximum Likelihood Analysis of Variance
Source	DF	Chi-Square	Pr > ChiSq
Intercept	2	39.88	<.0001
School	4	14.84	0.0050
Program	2	10.92	0.0043
Likelihood Ratio	4	1.78	0.7766

Figure 22.10: ANOVA Table

You can check the population and response profiles (not shown) to confirm that they are the same as those in Figure 22.8. The analysis of variance table is shown in Figure 22.10. The likelihood ratio chi-square statistic is 1.78 with a p-value of 0.7766, indicating a good fit; the Wald chi-square tests for the school and program effects are also significant. Since School has three levels, two parameters are estimated for each of the two logits they modeled, for a total of four degrees of freedom. Since Program has two levels, one parameter is estimated for each of the two logits, for a total of two degrees of freedom.

The CATMOD Procedure

Analysis of Maximum Likelihood Estimates
Effect	Parameter	Estimate	Standard Error	Chi- Square	Pr > ChiSq
Intercept	1	-0.7979	0.1465	29.65	<.0001
	2	-0.6589	0.1367	23.23	<.0001
School	3	-0.7992	0.2198	13.22	0.0003
	4	-0.2786	0.1867	2.23	0.1356
	5	0.2836	0.1899	2.23	0.1352
	6	-0.0985	0.1892	0.27	0.6028
Program	7	0.3737	0.1410	7.03	0.0080
	8	0.3713	0.1353	7.53	0.0061

Figure 22.11: Parameter Estimates

The parameter estimates and tests for individual parameters are displayed in Figure 22.11. The ordering of the parameters corresponds to the order of the population and response variables as shown in the profile tables (see Figure 22.8), with the levels of the response variables varying most rapidly. So, for the first response function, which is the logit that compares self to class, Parameter 1 is the intercept, Parameter 3 is the parameter for the differential effect for School=1, Parameter 5 is the parameter for the differential effect for School=2, and Parameter 7 is the parameter for the differential effect for Program=regular. The even parameters are interpreted similarly for the second logit, which compares team to class.

The Program variable (Parameters 7 and 8) has nearly the same effect on both logits, while School=1 (Parameters 3 and 4) has the largest effect of the schools.

Chapter Contents
Previous
Next
Top