Example 29.2: Normal Regression, Log Link

The GENMOD Procedure

Example 29.2: Normal Regression, Log Link

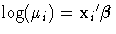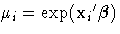Consider the following data, where x is an explanatory variable, and y is the response variable. It appears that y varies nonlinearly with x and that the variance is approximately constant. A normal distribution with a log link function is chosen to model these data; that is, $\log(\mu_i) = {x_{i}}'{{\beta}}$ so that $\mu_i = \exp({x_{i}}'{{\beta}})$ .

The following SAS statements produce the analysis with the normal distribution and log link:

   proc genmod data=nor;
      model y = x / dist = normal
                    link = log
                    ;
      output out = Residuals
             pred = Pred
             resraw = Resraw
             reschi = Reschi
             resdev = Resdev
             stdreschi = Stdreschi
             stdresdev = Stdresdev
             reslik = Reslik;
      proc print data=Residuals;
   run;

The OUTPUT statement is specified to produce a data set that contains predicted values and residuals for each observation. This data set can be useful for further analysis, such as residual plotting.

The output from these statements is displayed in Output 29.2.1.

Output 29.2.1: Log Linked Normal Regression

The GENMOD Procedure

Model Information
Data Set	WORK.NOR
Distribution	Normal
Link Function	Log
Dependent Variable	y
Observations Used	16

Criteria For Assessing Goodness Of Fit
Criterion	DF	Value	Value/DF
Deviance	14	52.3000	3.7357
Scaled Deviance	14	16.0000	1.1429
Pearson Chi-Square	14	52.3000	3.7357
Scaled Pearson X2	14	16.0000	1.1429
Log Likelihood		-32.1783

Analysis Of Parameter Estimates
Parameter	DF	Estimate	Standard Error	Wald 95% Confidence Limits		Chi-Square	Pr > ChiSq
Intercept	1	1.7214	0.0894	1.5461	1.8966	370.76	<.0001
x	1	0.3496	0.0206	0.3091	0.3901	286.64	<.0001
Scale	1	1.8080	0.3196	1.2786	2.5566

NOTE:

The scale parameter was estimated by maximum likelihood.

The PROC GENMOD scale parameter, in the case of the normal distribution, is the standard deviation. By default, the scale parameter is estimated by maximum likelihood. You can specify a fixed standard deviation by using the NOSCALE and SCALE= options in the MODEL statement.

Output 29.2.2: Data Set of Predicted Values and Residuals

Obs	x	y	Pred	Reschi	Resdev	Resraw	Stdreschi	Stdresdev	Reslik
1	0	5	5.5921	-0.59212	-0.59212	-0.59212	-0.34036	-0.34036	-0.34036
2	0	7	5.5921	1.40788	1.40788	1.40788	0.80928	0.80928	0.80928
3	0	9	5.5921	3.40788	3.40788	3.40788	1.95892	1.95892	1.95892
4	1	7	7.9324	-0.93243	-0.93243	-0.93243	-0.54093	-0.54093	-0.54093
5	1	10	7.9324	2.06757	2.06757	2.06757	1.19947	1.19947	1.19947
6	1	8	7.9324	0.06757	0.06757	0.06757	0.03920	0.03920	0.03920
7	2	11	11.2522	-0.25217	-0.25217	-0.25217	-0.14686	-0.14686	-0.14686
8	2	9	11.2522	-2.25217	-2.25217	-2.25217	-1.31166	-1.31166	-1.31166
9	3	16	15.9612	0.03878	0.03878	0.03878	0.02249	0.02249	0.02249
10	3	13	15.9612	-2.96122	-2.96122	-2.96122	-1.71738	-1.71738	-1.71738
11	3	14	15.9612	-1.96122	-1.96122	-1.96122	-1.13743	-1.13743	-1.13743
12	4	25	22.6410	2.35897	2.35897	2.35897	1.37252	1.37252	1.37252
13	4	24	22.6410	1.35897	1.35897	1.35897	0.79069	0.79069	0.79069
14	5	34	32.1163	1.88366	1.88366	1.88366	1.22914	1.22914	1.22914
15	5	32	32.1163	-0.11634	-0.11634	-0.11634	-0.07592	-0.07592	-0.07592
16	5	30	32.1163	-2.11634	-2.11634	-2.11634	-1.38098	-1.38098	-1.38098

The data set of predicted values and residuals (Output 29.2.2) is created by the OUTPUT statement. With this data set, you can construct residual plots using the GPLOT procedure to aid in assessing model fit. Note that raw, Pearson, and deviance residuals are equal in this example. This is a characteristic of the normal distribution and is not true in general for other distributions.

Chapter Contents
Previous
Next
Top