| Introduction to
Regression Procedures |
Introductory Example
Regression analysis is the analysis of the relationship
between one variable and another set of variables.
The relationship is expressed as an equation that predicts a
response variable (also called a dependent variable
or criterion) from a function of regressor variables
(also called independent variables, predictors, explanatory
variables, factors, or carriers) and parameters.
The parameters are adjusted so that a measure of fit is optimized.
For example, the equation for the ith observation might be
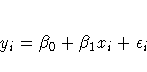
where yi is the response variable, xi is a regressor
variable, 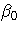 and
and 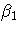 are unknown parameters
to be estimated, and
are unknown parameters
to be estimated, and 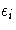 is an error term.
is an error term.
You might use regression analysis to find out how well you
can predict a child's weight if you know that child's height.
Suppose you collect your data by measuring
heights and weights of 19 school children.
You want to estimate the intercept 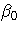 and the
slope
and the
slope 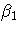 of a line described by the equation
of a line described by the equation
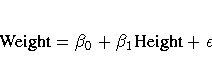
where
- Weight
- is the response variable.
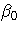 ,
, 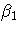
- are the unknown parameters.
- Height
- is the regressor variable.
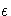
- is the unknown error.
The data are included in the following program.
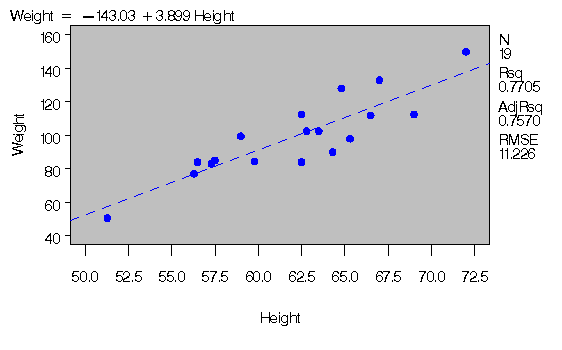
The results are displayed in Figure 3.1 and Figure 3.2.
data class;
input Name $ Height Weight Age;
datalines;
Alfred 69.0 112.5 14
Alice 56.5 84.0 13
Barbara 65.3 98.0 13
Carol 62.8 102.5 14
Henry 63.5 102.5 14
James 57.3 83.0 12
Jane 59.8 84.5 12
Janet 62.5 112.5 15
Jeffrey 62.5 84.0 13
John 59.0 99.5 12
Joyce 51.3 50.5 11
Judy 64.3 90.0 14
Louise 56.3 77.0 12
Mary 66.5 112.0 15
Philip 72.0 150.0 16
Robert 64.8 128.0 12
Ronald 67.0 133.0 15
Thomas 57.5 85.0 11
William 66.5 112.0 15
;
symbol1 v=dot c=blue height=3.5pct;
proc reg;
model Weight=Height;
plot Weight*Height/cframe=ligr;
run;
|
| The REG Procedure |
| Model: MODEL1 |
| Dependent Variable: Weight |
| Analysis of Variance |
| Source |
DF |
Sum of
Squares |
Mean
Square |
F Value |
Pr > F |
| Model |
1 |
7193.24912 |
7193.24912 |
57.08 |
<.0001 |
| Error |
17 |
2142.48772 |
126.02869 |
|
|
| Corrected Total |
18 |
9335.73684 |
|
|
|
| Root MSE |
11.22625 |
R-Square |
0.7705 |
| Dependent Mean |
100.02632 |
Adj R-Sq |
0.7570 |
| Coeff Var |
11.22330 |
|
|
| Parameter Estimates |
| Variable |
DF |
Parameter
Estimate |
Standard
Error |
t Value |
Pr > |t| |
| Intercept |
1 |
-143.02692 |
32.27459 |
-4.43 |
0.0004 |
| Height |
1 |
3.89903 |
0.51609 |
7.55 |
<.0001 |
|
Figure 3.1: Regression for Weight and Height Data
Figure 3.2: Regression for Weight and Height Data
Estimates of 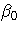 and
and 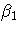 for
these data are b0=-143.0 and b1=3.9,
so the line is described by the equation
for
these data are b0=-143.0 and b1=3.9,
so the line is described by the equation
-
Weight = -143.0 + 3.9* Height
Regression is often used in an exploratory
fashion to look for empirical relationships, such
as the relationship between Height and Weight.
In this example, Height is not the cause of Weight.
You would need a controlled experiment to
confirm scientifically the relationship.
See the "Comments on Interpreting Regression Statistics" section for more information.
The method most commonly used to estimate the parameters is
to minimize the sum of squares of the differences between the
actual response value and the value predicted by the equation.
The estimates are called least-squares estimates, and
the criterion value is called the error sum of squares
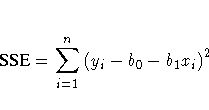
where
b0 and b1 are the estimates of
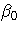 and
and 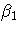 that minimize SSE.
that minimize SSE.
For a general discussion of the theory of least-squares
estimation of linear models and its application to
regression and analysis of variance, refer to one of the applied
regression texts, including Draper and Smith (1981), Daniel
and Wood (1980), Johnston (1972), and Weisberg (1985).
SAS/STAT regression procedures produce the following
information for a typical regression analysis:
- parameter estimates using the least-squares criterion
- estimates of the variance of the error term
- estimates of the variance or standard deviation of
the sampling distribution of the parameter estimates
- tests of hypotheses about the parameters
SAS/STAT regression procedures can produce
many other specialized diagnostic statistics, including
- collinearity diagnostics to measure how strongly
regressors are related to other regressors and how this
affects the stability and variance of the estimates (REG)
- influence diagnostics to measure how each
individual observation contributes to
determining the parameter estimates, the SSE,
and the fitted values (LOGISTIC, REG, RSREG)
- lack-of-fit diagnostics that measure the lack of fit
of the regression model by comparing the error variance
estimate to another pure error variance that is not
dependent on the form of the model (CATMOD, PROBIT, RSREG)
- diagnostic scatter plots that check the fit of the model
and highlighted scatter plots that identify particular
observations or groups of observations (REG)
- predicted and residual values, and confidence intervals for
the mean and for an individual value (GLM, LOGISTIC, REG)
- time-series diagnostics for equally spaced
time-series data that measure how much errors
may be related across neighboring observations.
These diagnostics can also measure functional
goodness of fit for data sorted by regressor
or response variables (REG, SAS/ETS procedures).
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
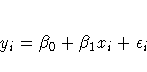
![]() and
and ![]() are unknown parameters
to be estimated, and
are unknown parameters
to be estimated, and ![]() is an error term.
is an error term.
![]() and the
slope
and the
slope ![]() of a line described by the equation
of a line described by the equation
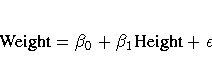
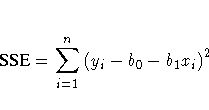
![]() and
and ![]() that minimize SSE.
that minimize SSE.