The KDE Procedure

Getting Started

The following example illustrates the basic features of PROC KDE. Assume that 1000 observations are simulated from a bivariate normal density with means (0,0), variances (10,10), and covariance 9. The SAS DATA step code to accomplish this is as follows:

   data k;
      seed = 1283470;
      do i = 1 to 1000;
         z1 = rannor(seed);
         z2 = rannor(seed);
         z3 = rannor(seed);
         x = 3*z1 + z2;
         y = 3*z1 + z3;
         output;
      end;
      drop seed;
   run;

The following PROC KDE code computes a bivariate kernel density estimate of these data:

   proc kde data=k out=o;
      var x y;
   run;

The output from this analysis is as follows.

The KDE Procedure

Inputs
Data Set	WORK.K
Number of Observations Used	1000
Variable 1	x
Variable 2	y
Bandwidth Method	Simple Normal Reference

The "Inputs" table lists basic information about the density fit, including the input data set, the number of observations, and the variables. The bandwidth method is the technique used to select the amount of smoothing in the estimate. A simple normal reference rule is used for bivariate smoothing.

The KDE Procedure

Controls
	x	y
Grid Points	60	60
Lower Grid Limit	-11.25	-10.05
Upper Grid Limit	9.1436	9.0341
Bandwidth Multiplier	1	1

The "Controls" table lists the primary numbers controlling the kernel density fit. Here a 60 ×60 grid is fit to the entire range of the data, and no adjustment is made to the default bandwidth.

The KDE Procedure

Statistics
	x	y
Mean	-0.075	-0.070
Variance	9.72	9.92
Standard Deviation	3.12	3.15
Range	20.39	19.09
Interquartile Range	4.46	4.51
Bandwidth	0.99	1.00

The "Statistics" table contains standard univariate statistics for each variable, as well as statistics associated with the density estimate. Note that the estimated variances for both X and Y are fairly close to the true values of 10.

The KDE Procedure

Bivariate Statistics
Covariance	8.88
Correlation	0.90

The "Bivariate Statistics" table lists the covariance and correlation between the two variables. Note that the estimated correlation is equal to its true value to two decimal places.

The KDE Procedure

Percentiles
	x	y
0.5	-7.71	-8.44
1.0	-7.08	-7.46
2.5	-6.17	-6.31
5.0	-5.28	-5.23
10.0	-4.18	-4.11
25.0	-2.24	-2.30
50.0	-0.11	-0.058
75.0	2.22	2.21
90.0	3.81	3.94
95.0	4.88	5.22
97.5	6.03	5.94
99.0	6.90	6.77
99.5	7.71	7.07

The "Percentiles" table lists percentiles for each variable.

The KDE Procedure

Levels
Percent	Density	Lower1	Lower2	Upper1	Upper2
1	0.001181	-8.14	-8.76	8.45	8.39
5	0.003028	-7.10	-7.14	7.07	6.77
10	0.004988	-6.41	-6.49	5.69	6.12
50	0.01592	-3.64	-3.58	3.96	3.86
90	0.02389	-1.22	-1.32	1.19	0.95
95	0.02525	-0.88	-0.99	0.50	0.62
99	0.02609	-0.53	-0.67	0.16	0.30
100	0.02630	-0.19	-0.35	-0.19	-0.35

The "Levels" table lists contours of the density corresponding to percentiles of the bivariate data, and the minimum and maximum values of each variable on those contours. For example, 5 percent of the observed data have a density value less than 0.0030. The minimum X and Y values on this contour are -7.10 and -7.14, respectively (the Lower1 and Lower2 columns), and the maximum values are 7.07 and 6.77, respectively (the Upper1 and Upper2 variables).

The output data set O from this analysis contains 3600 points containing the kernel density estimate. You can generate surface and contour plots of this estimate using SAS/GRAPH as follows:

   proc g3d data=o;
      plot y*x=density;
   run;

   proc gcontour data=o;
      plot y*x=density;
   run;

Figures 33.1 and 33.2 display these plots. Note that the correlation of 0.9 in the original data results in oval-shaped contours.

Figure 33.1: Surface plot of the bivariate kernel density estimate

Figure 33.2: Contour plot of the bivariate kernel density estimate

Suppose, after viewing Figures 33.1 and 33.2, that you would like a slightly smoother estimate. You could then rerun the analysis with a larger bandwidth:

   proc kde data=k out=o1 bwm=2,2;
      var x y;
   run;

The BWM=2,2 option requests bandwidth multipliers of 2 for both X and Y. The results of this fit and a subsequent call to PROC G3D produces Figure 33.3. Note that the small flattish area behind the main mode in Figure 33.1 has disappeared in Figure 33.3.

Figure 33.3: Surface plot of the bivariate kernel density estimate with additional smoothing

You can also use the results from the Levels table to plot specific contours corresponding to percentiles of the data. For example, the Levels table from the PROC KDE output using BWM=2,2 is as follows:

The KDE Procedure

Levels
Percent	Density	Lower1	Lower2	Upper1	Upper2
1	0.001238	-8.48	-8.76	8.45	8.39
5	0.003008	-7.10	-7.14	6.72	6.77
10	0.004625	-6.06	-5.85	6.03	6.12
50	0.01085	-3.30	-3.26	3.27	3.21
90	0.01430	-1.22	-1.32	1.19	0.95
95	0.01459	-0.88	-0.99	0.85	0.62
99	0.01478	-0.53	-0.67	0.50	0.30
100	0.01481	-0.19	-0.024	-0.19	-0.024

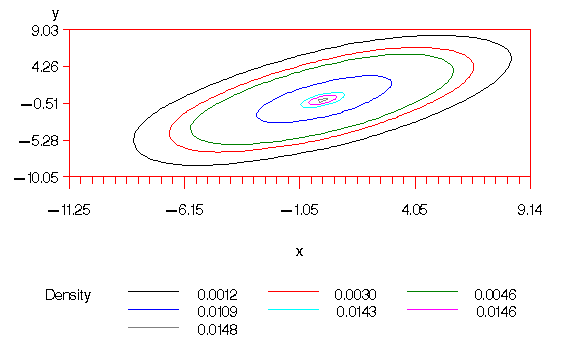
You can use the values from the Density column of this table with PROC GCONTOUR to plot the 1, 5, 10, 50, 90, 95, and 99 percent levels of the density:

   proc gcontour data=o1;
      plot y*x=density / levels=0.0012 0.0030 0.0046 0.0109
         0.0143 0.0146 0.0148;
   run;

This plot is displayed in Figure 33.4.

Figure 33.4: Contour plot of the bivariate kernel density estimate with additional smoothing and levels corresponding to percentiles

The next-to-outermost contour of Figure 33.4 represents an approximate 95 percent ellipsoid for X and Y.

Chapter Contents
Previous
Next
Top