The Nugget Effect

The KRIGE2D Procedure

The Nugget Effect

For all the variogram models considered previously, the following property holds:

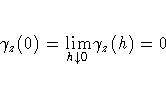
$\gamma_z(0) = \lim_{h \downarrow 0}\gamma_z(h) = 0$

However, a plot of the experimental semivariogram may indicate a discontinuity at h=0; that is, $\gamma_z(h) arrow c_n \gt 0$ as , while $\gamma_z(0)=0$ . The quantity c_n is called the "nugget effect"; this term is from mining geostatistics where nuggets literally exist, and it represents variations at a much smaller scale than any of the measured pairwise distances, that is, at distances $h \ll h_{min}$ , where

h_min = min_i,jh_ij = min_i,j| r_i-r_j|

There are conceptual and theoretical difficulties associated with a nonzero nugget effect; refer to Cressie (1993, section 2.3.1) and Christakos (1992, section 7.4.3) for details. There is no practical difficulty however; you simply visually extrapolate the experimental semivariogram as . The importance of availability of data at small lag distances is again illustrated.

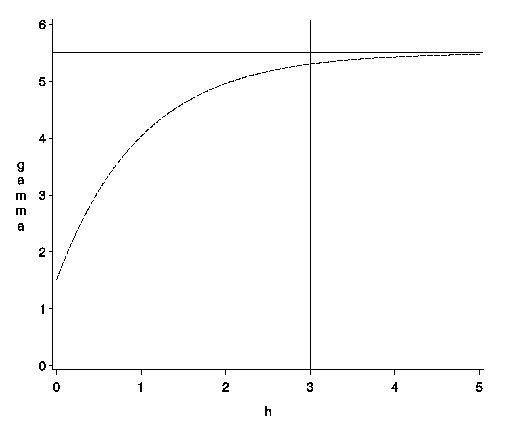
As an example, an exponential semivariogram with a nugget effect c_n has the form

$\gamma_z(h) = c_n + c_0[1-\exp(-\frac{h}{a_0})], h \gt 0$

and

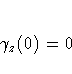
$\gamma_z(0) = 0$

This is illustrated in Figure 34.9 for parameters a₀=1, c₀=4, and nugget effect c_n=1.5.

Figure 34.9: Exponential Semivariogram Model with a Nugget Effect c_n=1.5

You can specify the nugget effect in PROC KRIGE2D with the NUGGET= option in the MODEL statement. It is a separate, additive term independent of direction; that is, it is isotropic. There is a way to approximate an anisotropic nugget effect; this is described in the following section.

Chapter Contents
Previous
Next
Top