Example 38.1: Engine Exhaust Emissions

The LOESS Procedure

Example 38.1: Engine Exhaust Emissions

Investigators studied the exhaust emissions of a one cylinder engine (Brinkman 1981). The SAS data set Gas contains the results data. The dependent variable, NOx, measures the concentration, in micrograms per joule, of nitric oxide and nitrogen dioxide normalized by the amount of work of the engine. The independent variable, E, is a measure of the richness of the air and fuel mixture.

   data Gas;
      input NOx E;
      format NOx f3.1;
      format E f3.1;
   datalines;
   4.818  0.831
   2.849  1.045
   3.275  1.021
   4.691  0.97
   4.255  0.825
   5.064  0.891
   2.118  0.71
   4.602  0.801
   2.286  1.074
   0.97   1.148
   3.965  1
   5.344  0.928
   3.834  0.767
   1.99   0.701
   5.199  0.807
   5.283  0.902
   3.752  0.997
   0.537  1.224
   1.64   1.089
   5.055  0.973
   4.937  0.98
   1.561  0.665
   ;

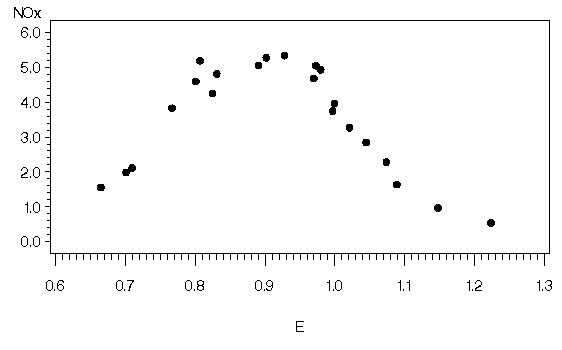
The following PROC GPLOT statements produce the simple scatter plot of these data, displayed in Output 38.1.1.

   
   symbol1 color=black value=dot ;  
   proc gplot data=Gas;
      plot NOx*E;
   run;

Output 38.1.1: Scatter Plot of Gas Data

The following statements fit two loess models for these data. Because this is a small data set, it is reasonable to do direct fitting at every data point. As there is substantial curvature in the data, quadratic local polynomials are used. An ODS OUTPUT statement creates two output data sets containing the "Output Statistics" and "Fit Summary" tables.

   proc loess data=Gas;
      ods output OutputStatistics = GasFit
                 FitSummary=Summary; 
      model NOx = E / degree=2 direct smooth = 0.6 1.0
                      alpha=.01 all details;
   run;

The "Fit Summary" table for smoothing parameter 0.6, shown in Output 38.1.2, records the fitting parameters specified and some overall fit statistics.

Output 38.1.2: Fit Summary Table

The LOESS Procedure

Smoothing Parameter: 0.6

Dependent Variable: NOx

Fit Summary
Fit Method	Direct
Number of Observations	22
Degree of Local Polynomials	2
Smoothing Parameter	0.60000
Points in Local Neighborhood	13
Residual Sum of Squares	1.71852
Trace[L]	6.42184
Delta1	15.12582
Delta2	14.73089
Equivalent Number of Parameters	5.96950
Lookup Degrees of Freedom	15.53133
Residual Standard Error	0.33707

The matrix L referenced in the "Fit Summary" table is the smoothing matrix. This matrix satisfies

$\hat{y}=L y$

where y is the vector of observed values and $\hat{y}$ is the corresponding vector of predicted values of the dependent variable. The quantities

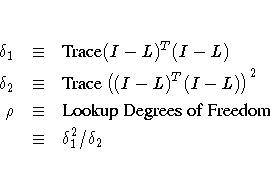
$\delta_1 & \equiv & {Trace} (I-L)^T(I-L) \ \delta_2 & \equiv & {Trace} ((I-L)^T... ...\ \rho & \equiv & {Lookup Degrees of Freedom} \ & \equiv & \delta_1^2/ \delta_2$

in the "Fit Summary" table are used in doing statistical inference.

The equivalent number of parameters and residual standard error in the "Fit Summary" table are defined by

${Equivalent Number of Parameters} & \equiv & {Trace} L^T L \ {Residual Standard Error} & \equiv & \sqrt { {Residual SS} / \delta_1 }$

The "Output Statistics" table for smoothing parameter 0.6 is shown in Output 38.1.3. Note that, as the ALL option in the MODEL statement is specified, this table includes all the relevant optional columns. Furthermore, because the ALPHA=0.01 option is specified in the MODEL statement, the confidence limits in this table are 99% limits.

Output 38.1.3: Output Statistics Table

The LOESS Procedure

Smoothing Parameter: 0.6

Dependent Variable: NOx

Output Statistics
Obs	E	NOx	Predicted NOx	Estimated Prediction Std Deviation	Residual	t Value	99% Confidence Limits
1	0.8	4.8	4.87377	0.15528	-0.05577	-0.36	4.41841	5.32912
2	1.0	2.8	2.81984	0.15380	0.02916	0.19	2.36883	3.27085
3	1.0	3.3	3.48153	0.15187	-0.20653	-1.36	3.03617	3.92689
4	1.0	4.7	4.73249	0.13923	-0.04149	-0.30	4.32419	5.14079
5	0.8	4.3	4.82305	0.15278	-0.56805	-3.72	4.37503	5.27107
6	0.9	5.1	5.18561	0.19337	-0.12161	-0.63	4.61855	5.75266
7	0.7	2.1	2.51120	0.15528	-0.39320	-2.53	2.05585	2.96655
8	0.8	4.6	4.48267	0.15285	0.11933	0.78	4.03444	4.93089
9	1.1	2.3	2.12619	0.16683	0.15981	0.96	1.63697	2.61541
10	1.1	1.0	0.97120	0.18134	-0.00120	-0.01	0.43942	1.50298
11	1.0	4.0	4.09987	0.13477	-0.13487	-1.00	3.70467	4.49507
12	0.9	5.3	5.31258	0.17283	0.03142	0.18	4.80576	5.81940
13	0.8	3.8	3.84572	0.14929	-0.01172	-0.08	3.40794	4.28350
14	0.7	2.0	2.26578	0.16712	-0.27578	-1.65	1.77571	2.75584
15	0.8	5.2	4.58394	0.15363	0.61506	4.00	4.13342	5.03445
16	0.9	5.3	5.24741	0.19319	0.03559	0.18	4.68089	5.81393
17	1.0	3.8	4.16979	0.13478	-0.41779	-3.10	3.77457	4.56502
18	1.2	0.5	0.53059	0.32170	0.00641	0.02	-0.41278	1.47397
19	1.1	1.6	1.83157	0.17127	-0.19157	-1.12	1.32933	2.33380
20	1.0	5.1	4.66733	0.13735	0.38767	2.82	4.26456	5.07010
21	1.0	4.9	4.52385	0.13556	0.41315	3.05	4.12632	4.92139
22	0.7	1.6	1.19888	0.26774	0.36212	1.35	0.41375	1.98401

Plots of the data points and fitted models with 99% confidence bands are shown in Output 38.1.4.

   proc sort data=GasFit;
      by SmoothingParameter E;
   run;  

   symbol1 color=black value=dot ;  
   symbol2 color=black interpol=spline value=none;  
   symbol3 color=green interpol=spline value=none; 
   symbol4 color=green interpol=spline value=none; 

   %let opts=vaxis=axis1 hm=3 vm=3 overlay;

   goptions nodisplay hsize=3.75; 
   axis1 label=(angle=90 rotate=0); 

   proc gplot data=GasFit;
      by SmoothingParameter;
      plot (DepVar Pred LowerCL UpperCL)*E/ &opts name='fitGas';
   run; quit;

   goptions display hsize=0 hpos=0;
   proc greplay nofs tc=sashelp.templt template=h2;
       igout gseg;
       treplay 1:fitGas 2:fitGas1;
   run; quit;

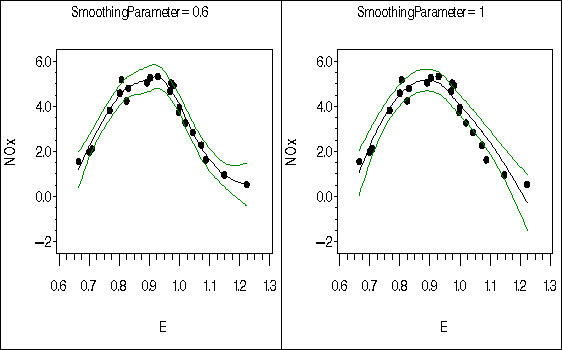
Output 38.1.4: Loess Fits with 99% Confidence Bands for Gas Data

It is evident from the preceding figure that the better fit is obtained with smoothing parameter 0.6. Scatter plots of the fit residuals confirm this observation. Note also that PROC LOESS is again used to produce the Residual variable on these plots.

 
   proc loess data=GasFit;
      by SmoothingParameter;
      ods output OutputStatistics=residout;
      model Residual=E;                
   run; 

   axis1 label = (angle=90 rotate=0)
         order = (-1 to 1 by 0.5); 
   goptions nodisplay hsize=3.75; 
   proc gplot data=residout;           
      by SmoothingParameter;
      plot  DepVar*E Pred*E/ &opts vref=0 lv=2 vm=1 
                             name='resGas';
   run; quit;

   goptions display hsize=0 hpos=0;
   proc greplay nofs tc=sashelp.templt template=h2;
       igout gseg;
       treplay 1:resGas 2:resGas1;
   run; quit;

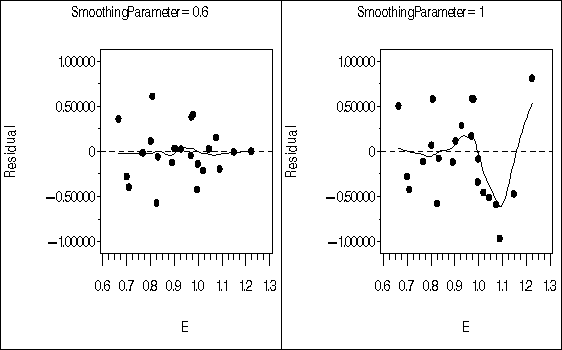
Output 38.1.5: Scatter Plots of Loess Fit Residuals

The residual plots show that with smoothing parameter 1, the loess model exhibits a lack of fit. Analysis of variance can be used to compare the model with smoothing parameter 1, which serves as the null model, to the model with smoothing parameter 0.6.

The statistic

$F=\frac {({rss}^{(n)}-{rss}) / (\delta_1^{(n)}-\delta_1)} { {rss}/ \delta_1}$

has a distribution that is well approximated by an F distribution with

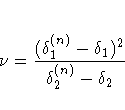
$\nu=\frac {(\delta_1^{(n)}-\delta_1)^2} {\delta_2^{(n)}-\delta_2}$

numerator degrees of freedom and $\rho$ denominator degrees of freedom (Cleveland and Grosse 1991). Here quantities with superscript n refer to the null model, rss is the residual sum of squares, and $\delta_1$ , $\delta_2$ , and $\rho$ are as previously defined.

The "Fit Summary" tables contain the information needed to carry out such an analysis. These tables have been captured in the output data set named Summary using an ODS OUTPUT statement. The following statements extract the relevant information from this data set and carry out the analysis of variance:

  data h0 h1;
    set Summary(keep=SmoothingParameter Label1 nValue1
                where=(Label1 in ('Residual Sum of Squares',
                       'Delta1',
                       'Delta2',
                       'Lookup Degrees of Freedom')));
    if SmoothingParameter = 1 then output h0;
    else output h1;
  run;

  proc transpose data=h0(drop=SmoothingParameter Label1)
                 out=h0;

  data h0(drop=_NAME_); set h0;
    rename Col1 = RSSNull
           Col2 = delta1Null
           Col3 = delta2Null;

  proc transpose data=h1(drop=SmoothingParameter Label1)
                 out=h1;

  data h1(drop=_NAME_); set h1;
    rename Col1 = RSS
           Col2 = delta1
           Col3 = delta2
           Col4 = rho;

  data ftest; merge h0 h1;
    nu = (delta1Null - delta1)**2 / (delta2Null - delta2);
    Numerator = (RSSNull - RSS)/(delta1Null - delta1);
    Denominator = RSS/delta1;
    FValue = Numerator / Denominator;
    PValue = 1 - ProbF(FValue, nu, rho);
    label nu = 'Num DF'
          rho = 'Den DF'
          FValue = 'F Value'
          PValue = 'Pr > F';

  proc print data=ftest label;
    var nu rho Numerator Denominator FValue PValue;
    format nu rho FValue 7.2 PValue 6.4;
  run;

The results are shown in Output 38.1.6.

Output 38.1.6: Test ANOVA for LOESS MODELS of Gas Data

Obs	Num DF	Den DF	Numerator	Denominator	F Value	Pr > F
1	2.67	15.53	1.05946	0.11362	9.32	0.0012

The highly significant p-value confirms that the loess model with smoothing parameter 0.6 provides a better fit than the model with smoothing parameter 1.

Chapter Contents
Previous
Next
Top