Example 39.3: Logistic Modeling with Categorical Predictors
Consider a study of the analgesic effects of treatments on
elderly patients with neuralgia.
Two test treatments and a placebo are compared. The response
variable is whether the patient reported pain or not.
Researchers recorded
age and gender of the patients
and the duration of complaint before the treatment began.
The data, consisting of 60 patients, are contained in the
data set Neuralgia.
Data Neuralgia;
input Treatment $ Sex $ Age Duration Pain $ @@;
datalines;
P F 68 1 No B M 74 16 No P F 67 30 No
P M 66 26 Yes B F 67 28 No B F 77 16 No
A F 71 12 No B F 72 50 No B F 76 9 Yes
A M 71 17 Yes A F 63 27 No A F 69 18 Yes
B F 66 12 No A M 62 42 No P F 64 1 Yes
A F 64 17 No P M 74 4 No A F 72 25 No
P M 70 1 Yes B M 66 19 No B M 59 29 No
A F 64 30 No A M 70 28 No A M 69 1 No
B F 78 1 No P M 83 1 Yes B F 69 42 No
B M 75 30 Yes P M 77 29 Yes P F 79 20 Yes
A M 70 12 No A F 69 12 No B F 65 14 No
B M 70 1 No B M 67 23 No A M 76 25 Yes
P M 78 12 Yes B M 77 1 Yes B F 69 24 No
P M 66 4 Yes P F 65 29 No P M 60 26 Yes
A M 78 15 Yes B M 75 21 Yes A F 67 11 No
P F 72 27 No P F 70 13 Yes A M 75 6 Yes
B F 65 7 No P F 68 27 Yes P M 68 11 Yes
P M 67 17 Yes B M 70 22 No A M 65 15 No
P F 67 1 Yes A M 67 10 No P F 72 11 Yes
A F 74 1 No B M 80 21 Yes A F 69 3 No
;
The data set Neuralgia contains five variables: Treatment,
Sex,
Age, Duration, and Pain. The last variable, Pain,
is the response variable.
A specification of
Pain=Yes indicates there was pain, and Pain=No
indicates no pain.
The variable Treatment is a categorical variable with three
levels: A and B
represent the two test treatments, and P represents the placebo treatment.
The gender of the patients is given by the categorical variable Sex.
The variable Age is the
age of the patients, in years, when treatment began.
The duration of complaint, in months, before the treatment began is given
by the variable Duration. The following statements use the
LOGISTIC procedure to fit a two-way logit with interaction model for the
effect of Treatment and Sex, with Age and
Duration as covariates. The categorical variables Treatment and
Sex are
declared in the CLASS statement.
proc logistic data=Neuralgia;
class Treatment Sex;
model Pain= Treatment Sex Treatment*Sex Age Duration / expb;
run;
In this analysis, PROC LOGISTIC models the probability of
no pain (Pain=No).
By default, effect coding is used
to represent the
CLASS variables. Two dummy variables are created for Treatment
and one
for Sex, as shown in Output 39.3.1.
Output 39.3.1: Effect Coding of CLASS Variables
|
| Class Level Information |
| Class |
Value |
Design Variables |
| 1 |
2 |
| Treatment |
A |
1 |
0 |
| |
B |
0 |
1 |
| |
P |
-1 |
-1 |
| Sex |
F |
1 |
|
| |
M |
-1 |
|
|
PROC LOGISTIC displays
a table of the Type III analysis of effects based on the Wald
test (Output 39.3.2). Note that the Treatment*Sex interaction
and the duration of complaint are not statistically significant
(p=0.9318 and p=0.8752, respectively). This indicates that there is no
evidence that the treatments affect pain differently in men and women,
and no evidence that the pain outcome is related to the duration of pain.
Output 39.3.2: Wald Tests of Individual Effects
|
| Type III Analysis of Effects |
| Effect |
DF |
Wald
Chi-Square |
Pr > ChiSq |
| Treatment |
2 |
11.9886 |
0.0025 |
| Sex |
1 |
5.3104 |
0.0212 |
| Treatment*Sex |
2 |
0.1412 |
0.9318 |
| Age |
1 |
7.2744 |
0.0070 |
| Duration |
1 |
0.0247 |
0.8752 |
|
Parameter estimates are displayed in Output 39.3.3. The Exp(Est) column
contains the exponentiated parameter estimates. These values may, but
do not
necessarily, represent odds ratios for the corresponding variables. For
continuous explanatory variables, the Exp(Est) value corresponds to the
odds ratio for a unit increase of the corresponding variable.
For CLASS variables using
the effect coding, the Exp(Est) values have no direct interpretation as
a comparison of levels. However, when the reference coding is used,
the Exp(Est) values represent
the odds ratio between the corresponding level and the last level.
Following the parameter estimates table, PROC LOGISTIC displays
the odds ratio
estimates for those variables that are not
involved in any interaction terms.
If the variable is a CLASS variable, the odds ratio estimate comparing
each level with the last level is computed regardless of the coding
scheme.
In this analysis, since the model contains the Treatment*Sex
interaction term, the odds ratios for Treatment and Sex
were not computed.
The odds ratio
estimates for Age and Duration are precisely the values
given in the Exp(Est)
column in the parameter estimates table.
Output 39.3.3: Parameter Estimates with Effect Coding
|
| Analysis of Maximum Likelihood Estimates |
| Parameter |
|
|
DF |
Estimate |
Standard
Error |
Chi-Square |
Pr > ChiSq |
Exp(Est) |
| Intercept |
|
|
1 |
19.2236 |
7.1315 |
7.2661 |
0.0070 |
2.232E8 |
| Treatment |
A |
|
1 |
0.8483 |
0.5502 |
2.3773 |
0.1231 |
2.336 |
| Treatment |
B |
|
1 |
1.4949 |
0.6622 |
5.0956 |
0.0240 |
4.459 |
| Sex |
F |
|
1 |
0.9173 |
0.3981 |
5.3104 |
0.0212 |
2.503 |
| Treatment*Sex |
A |
F |
1 |
-0.2010 |
0.5568 |
0.1304 |
0.7180 |
0.818 |
| Treatment*Sex |
B |
F |
1 |
0.0487 |
0.5563 |
0.0077 |
0.9302 |
1.050 |
| Age |
|
|
1 |
-0.2688 |
0.0996 |
7.2744 |
0.0070 |
0.764 |
| Duration |
|
|
1 |
0.00523 |
0.0333 |
0.0247 |
0.8752 |
1.005 |
| Odds Ratio Estimates |
| Effect |
Point Estimate |
95% Wald
Confidence Limits |
| Age |
0.764 |
0.629 |
0.929 |
| Duration |
1.005 |
0.942 |
1.073 |
|
The following PROC LOGISTIC statements illustrate the use of forward selection
on the data set Neuralgia
to identify the effects that differentiate the two Pain responses.
The
option SELECTION=FORWARD is specified to carry out the forward selection.
Although it is the default, the option RULE=SINGLE is explicitly
specified
to select one effect in each
step where the selection must maintain model hierarchy.
The term Treatment|Sex@2 illustrates another way
to specify main
effects and two-way interaction as is available in other procedures
such as PROC GLM. (Note that, in this case, the "@2" is
unnecessary because no interactions besides the two-way interaction are possible).
proc logistic data=Neuralgia;
class Treatment Sex;
model Pain=Treatment|Sex@2 Age Duration/selection=forward
rule=single
expb;
run;
Results of the forward selection process are summarized in Output 39.3.4.
The variable Treatment is selected first, followed by
Age and
then Sex. The results are consistent with the previous analysis
(Output 39.3.2) in which
the Treatment*Sex
interaction and Duration are not statistically
significant.
Output 39.3.4: Effects Selected into the Model
|
| Forward Selection Procedure |
| Summary of Forward Selection |
| Step |
Effect
Entered |
DF |
Number
In |
Score
Chi-Square |
Pr > ChiSq |
| 1 |
Treatment |
2 |
1 |
13.7143 |
0.0011 |
| 2 |
Age |
1 |
2 |
10.6038 |
0.0011 |
| 3 |
Sex |
1 |
3 |
5.9959 |
0.0143 |
|
Output 39.3.5 shows the Type III analysis of effects, the parameter
estimates, and the odds ratio estimates for the selected model. All three
variables, Treatment, Age, and Sex,
are statistically significant at
the 0.05
level (p=0.0011, p=0.0011, and p=0.0143, respectively).
Since the selected model does not contain the Treatment*Sex
interaction,
odds ratios for Treatment and Sex are computed.
The estimated odds ratio
is 24.022 for treatment A versus placebo, 41.528 for
Treatment B versus
placebo, and 6.194 for female patients versus male patients.
Note that these
odds ratio estimates are not the same as the corresponding values in the
Exp(Est) column in the parameter estimates table because effect coding
was used.
From Output 39.3.5, it is evident that
both Treatment A and Treatment B are better than the placebo
in reducing
pain; females tend to have better improvement than males; and
younger patients are
faring better than older patients.
Output 39.3.5: Type III Effects and Parameter Estimates with Effect Coding
|
| Forward Selection Procedure |
| Type III Analysis of Effects |
| Effect |
DF |
Wald
Chi-Square |
Pr > ChiSq |
| Treatment |
2 |
12.6928 |
0.0018 |
| Sex |
1 |
5.3013 |
0.0213 |
| Age |
1 |
7.6314 |
0.0057 |
| Analysis of Maximum Likelihood Estimates |
| Parameter |
|
|
DF |
Estimate |
Standard
Error |
Chi-Square |
Pr > ChiSq |
Exp(Est) |
| Intercept |
|
|
1 |
19.0804 |
6.7882 |
7.9007 |
0.0049 |
1.9343E8 |
| Treatment |
A |
|
1 |
0.8772 |
0.5274 |
2.7662 |
0.0963 |
2.404 |
| Treatment |
B |
|
1 |
1.4246 |
0.6036 |
5.5711 |
0.0183 |
4.156 |
| Sex |
F |
|
1 |
0.9118 |
0.3960 |
5.3013 |
0.0213 |
2.489 |
| Age |
|
|
1 |
-0.2650 |
0.0959 |
7.6314 |
0.0057 |
0.767 |
| Odds Ratio Estimates |
| Effect |
Point Estimate |
95% Wald
Confidence Limits |
| Treatment A vs P |
24.022 |
3.295 |
175.121 |
| Treatment B vs P |
41.528 |
4.500 |
383.262 |
| Sex F vs M |
6.194 |
1.312 |
29.248 |
| Age |
0.767 |
0.636 |
0.926 |
|
Finally,
PROC LOGISTIC is invoked to refit the previously selected model
using reference coding for the CLASS variables. Two CONTRAST statments are
specified. The one labeled 'Pairwise' specifies three rows
in the contrast matrix, L, for
all the pairwise comparisons between the three levels of Treatment.
The contrast labeled 'Female vs Male' compares female to male patients.
The option ESTIMATE=EXP is specified in both CONTRAST statements
to exponentiate the estimates of 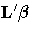 .With the given specification of
contrast coefficients, the first row of the 'Pairwise' CONTRAST
statement corresponds to the odds ratio of A versus P,
the second row corresponds to B versus P, and the third row corresponds
to A versus B. There is only one row in the 'Female vs Male' CONTRAST
statement, and it corresponds to the
odds ratio comparing female to male patients.
.With the given specification of
contrast coefficients, the first row of the 'Pairwise' CONTRAST
statement corresponds to the odds ratio of A versus P,
the second row corresponds to B versus P, and the third row corresponds
to A versus B. There is only one row in the 'Female vs Male' CONTRAST
statement, and it corresponds to the
odds ratio comparing female to male patients.
proc logistic data=Neuralgia;
class Treatment Sex /param=ref;
model Pain= Treatment Sex age;
contrast 'Pairwise' Treatment 1 0 -1,
Treatment 0 1 -1,
Treatment 1 -1 0 / estimate=exp;
contrast 'Female vs Male' Sex 1 -1 / estimate=exp;
run;
Output 39.3.6: Reference Coding of CLASS Variables
|
| Class Level Information |
| Class |
Value |
Design Variables |
| 1 |
2 |
| Treatment |
A |
1 |
0 |
| |
B |
0 |
1 |
| |
P |
0 |
0 |
| Sex |
F |
1 |
|
| |
M |
0 |
|
|
The reference coding is shown in Output 39.3.6.
The Type III analysis of effects, the parameter estimates
for the reference coding, and the odds ratio estimates are displayed in
Output 39.3.7.
Although the parameter estimates are different (because of the different
parameterizations), the "Type III Analysis of Effects" table and the
"Odds Ratio" table remain the same as in Output 39.3.5.
With effect coding, the treatment A parameter estimate (0.8772) estimates
the effect of treatment A compared to the average effect of treatments
A, B, and placebo. The treatment A estimate (3.1790)
under the reference coding estimates
the difference in effect of treatment A and the placebo treatment.
Output 39.3.7: Type III Effects and Parameter Estimates with
Reference Coding
|
| Type III Analysis of Effects |
| Effect |
DF |
Wald
Chi-Square |
Pr > ChiSq |
| Treatment |
2 |
12.6928 |
0.0018 |
| Sex |
1 |
5.3013 |
0.0213 |
| Age |
1 |
7.6314 |
0.0057 |
| Analysis of Maximum Likelihood Estimates |
| Parameter |
|
DF |
Estimate |
Standard
Error |
Chi-Square |
Pr > ChiSq |
| Intercept |
|
1 |
15.8669 |
6.4056 |
6.1357 |
0.0132 |
| Treatment |
A |
1 |
3.1790 |
1.0135 |
9.8375 |
0.0017 |
| Treatment |
B |
1 |
3.7264 |
1.1339 |
10.8006 |
0.0010 |
| Sex |
F |
1 |
1.8235 |
0.7920 |
5.3013 |
0.0213 |
| Age |
|
1 |
-0.2650 |
0.0959 |
7.6314 |
0.0057 |
| Odds Ratio Estimates |
| Effect |
Point Estimate |
95% Wald
Confidence Limits |
| Treatment A vs P |
24.022 |
3.295 |
175.121 |
| Treatment B vs P |
41.528 |
4.500 |
383.262 |
| Sex F vs M |
6.194 |
1.312 |
29.248 |
| Age |
0.767 |
0.636 |
0.926 |
|
Output 39.3.8 contains two tables:
the "Contrast Test Results" table and the
"Contrast Rows Estimation and Testing Results" table.
The former contains
the overall Wald test for each CONTRAST statement. Although three
rows are specifed in the
'Pairwise' CONTRAST statement, there are only two degrees of
freedom, and the Wald test result is identical to the Type III analysis
of Treatment in Output 39.3.7.
The latter table contains estimates and tests of
individual contrast rows.
The estimates for the first two rows of the
'Pairwise' CONTRAST
statement are the
same as those given in the "Odds Ratio Estimates" table
(in Output 39.3.7). Both treatments
A and B are highly effective over placebo in reducing
pain. The
third row estimates the odds ratio comparing A to B.
The 95% confidence interval for this odds ratio
is (0.0932, 3.5889), indicating that the pain reduction
effects of these two test treatments
are not that different. Again, the 'Female vs Male' contrast
shows that female patients fared better in obtaining relief from pain
than male patients.
Output 39.3.8: Results of CONTRAST Statements
|
| Contrast Test Results |
| Contrast |
DF |
Wald
Chi-Square |
Pr > ChiSq |
| Pairwise |
2 |
12.6928 |
0.0018 |
| Female vs Male |
1 |
5.3013 |
0.0213 |
| Contrast Rows Estimation and Testing Results |
| Contrast |
Type |
Row |
Estimate |
Standard
Error |
Alpha |
Lower Limit |
Upper Limit |
Wald
Chi-Square |
Pr > ChiSq |
| Pairwise |
EXP |
1 |
24.0218 |
24.3473 |
0.05 |
3.2951 |
175.1 |
9.8375 |
0.0017 |
| Pairwise |
EXP |
2 |
41.5284 |
47.0877 |
0.05 |
4.4998 |
383.3 |
10.8006 |
0.0010 |
| Pairwise |
EXP |
3 |
0.5784 |
0.5387 |
0.05 |
0.0932 |
3.5889 |
0.3455 |
0.5567 |
| Female vs Male |
EXP |
1 |
6.1937 |
4.9053 |
0.05 |
1.3116 |
29.2476 |
5.3013 |
0.0213 |
|
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.