Example 39.6: ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits

The LOGISTIC Procedure

Example 39.6: ROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence Limits

This example plots an ROC curve, estimates a customized odds ratio, produces the traditional goodness-of-fit analysis, displays the generalized R² measures for the fitted model, and calculates the normal confidence intervals for the regression parameters. The data consist of three variables: n (number of subjects in a sample), disease (number of diseased subjects in the sample), and age (age for the sample). A linear logistic regression model is used to study the effect of age on the probability of contracting the disease.

The SAS code is as follows:

   data Data1;
      input disease n age;
      datalines;
    0 14 25
    0 20 35
    0 19 45
    7 18 55
    6 12 65
   17 17 75
   ;

   proc logistic data=Data1;
      model disease/n=age / scale=none
                            clparm=wald
                            clodds=pl
                            rsquare
                            outroc=roc1;
      units age=10;
   run;

The option SCALE=NONE is specified to produce the deviance and Pearson goodness-of-fit analysis without adjusting for overdispersion. The RSQUARE option is specified to produce generalized R² measures of the fitted model. The CLPARM=WALD option is specified to produce the Wald confidence intervals for the regression parameters. The UNITS statement is specified to produce customized odds ratio estimates for a change of 10 years in the age variable, and the CLODDS=PL option is specified to produce profile likelihood confidence limits for the odds ratio. The OUTROC= option outputs the data for the ROC curve to the SAS data set, roc1.

Results are shown in Output 39.6.1 and Output 39.6.2.

Output 39.6.1: Deviance and Pearson Goodness-of-Fit Analysis

The LOGISTIC Procedure

Deviance and Pearson Goodness-of-Fit Statistics
Criterion	DF	Value	Value/DF	Pr > ChiSq
Deviance	4	7.7756	1.9439	0.1002
Pearson	4	6.6020	1.6505	0.1585

Number of events/trials observations: 6

Output 39.6.2: R-Square, Confidence Intervals, and Customized Odds Ratio

Model Fit Statistics
Criterion	Intercept Only	Intercept and Covariates
AIC	124.173	52.468
SC	126.778	57.678
-2 Log L	122.173	48.468

R-Square	0.5215	Max-rescaled R-Square	0.7394

Testing Global Null Hypothesis: BETA=0
Test	Chi-Square	DF	Pr > ChiSq
Likelihood Ratio	73.7048	1	<.0001
Score	55.3274	1	<.0001
Wald	23.3475	1	<.0001

Analysis of Maximum Likelihood Estimates
Parameter	DF	Estimate	Standard Error	Chi-Square	Pr > ChiSq
Intercept	1	-12.5016	2.5555	23.9317	<.0001
age	1	0.2066	0.0428	23.3475	<.0001

Association of Predicted Probabilities and Observed Responses
Percent Concordant	92.6	Somers' D	0.906
Percent Discordant	2.0	Gamma	0.958
Percent Tied	5.4	Tau-a	0.384
Pairs	2100	c	0.953

Wald Confidence Interval for Parameters
Parameter	Estimate	95% Confidence Limits
Intercept	-12.5016	-17.5104	-7.4929
age	0.2066	0.1228	0.2904

Profile Likelihood Confidence Interval for Adjusted Odds Ratios
Effect	Unit	Estimate	95% Confidence Limits
age	10.0000	7.892	3.881	21.406

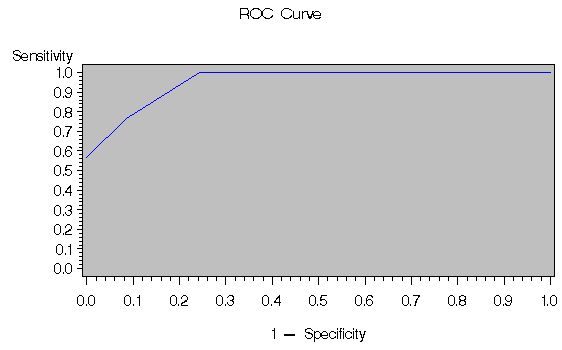
The ROC curve is plotted by the GPLOT procedure, and the plot is shown in Output 39.6.3.

   symbol1 i=join v=none c=blue;
   proc gplot data=roc1;
      title 'ROC Curve';
      plot _sensit_*_1mspec_=1 / vaxis=0 to 1 by .1 cframe=ligr;
   run;

Output 39.6.3: Receiver Operating Characteristic Curve

Note that the area under the ROC curve is given by the statistic c in the "Association of Predicted Probabilities and Observed Responses" table. In this example, the area under the ROC curve is 0.953.

Chapter Contents
Previous
Next
Top