Example 39.10: Complementary Log-Log Model for Infection Rates

The LOGISTIC Procedure

Example 39.10: Complementary Log-Log Model for Infection Rates

Antibodies produced in response to an infectious disease like malaria remain in the body after the individual has recovered from the disease. A serological test detects the presence or absence of such antibodies. An individual with such antibodies is termed seropositive. In areas where the disease is endemic, the inhabitants are at fairly constant risk of infection. The probability of an individual never having been infected in Y years is $\exp(-\mu Y )$ , where $\mu$ is the mean number of infections per year (refer to the appendix of Draper et al. 1972). Rather than estimating the unknown $\mu$ , it is of interest to epidemiologists to estimate the probability of a person living in the area being infected in one year. This infection rate $\gamma$ is given by

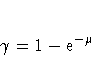
$\gamma = 1-{\rm e}^{-\mu}$

The following SAS statements create the data set sero, which contains the results of a serological survey of malarial infection. Individuals of nine age groups were tested. Variable A represents the midpoint of the age range for each age group. Variable N represents the number of individuals tested in each age group, and variable R represents the number of individuals that are seropositive.

   data sero;
      input group A N R;
      X=log(A);
      label X='Log of Midpoint of Age Range';
      datalines;
   1  1.5  123  8
   2  4.0  132  6
   3  7.5  182 18
   4 12.5  140 14
   5 17.5  138 20
   6 25.0  161 39
   7 35.0  133 19
   8 47.0   92 25
   9 60.0   74 44
   ;

For the ith group with age midpoint A_i, the probability of being seropositive is $p_i=1-\exp(-\mu A_i)$ . It follows that

log(-log(1-p_i)) = log(u) + log(A_i)

By fitting a binomial model with a complementary log-log link function and by using X=log(A) as an offset term, you can estimate $\beta_0=\log(\mu)$ as an intercept parameter. The following SAS statements invoke PROC LOGISTIC to compute the maximum likelihood estimate of $\beta_0$ . The LINK=CLOGLOG option is specified to request the complementary log-log link function. Also specified is the CLPARM=PL option, which requests the profile likelihood confidence limits for $\beta_0$ .

   proc logistic data=sero;
      model R/N= / offset=X
                   link=cloglog
                   clparm=pl
                   scale=none;
      title 'Constant Risk of Infection';
   run;

Output 39.10.1: Modeling Constant Risk of Infection

Constant Risk of Infection

The LOGISTIC Procedure

Model Information
Data Set	WORK.SERO
Response Variable (Events)	R
Response Variable (Trials)	N
Number of Observations	9
Offset Variable	X	Log of Midpoint of Age Range
Link Function	Complementary log-log
Optimization Technique	Fisher's scoring

Response Profile
Ordered Value	Binary Outcome	Total Frequency
1	Event	193
2	Nonevent	982

Intercept-Only Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.

-2 Log L = 967.1158

Deviance and Pearson Goodness-of-Fit Statistics
Criterion	DF	Value	Value/DF	Pr > ChiSq
Deviance	8	41.5032	5.1879	<.0001
Pearson	8	50.6883	6.3360	<.0001

Number of events/trials observations: 9

Analysis of Maximum Likelihood Estimates
Parameter	DF	Estimate	Standard Error	Chi-Square	Pr > ChiSq
Intercept	1	-4.6605	0.0725	4133.5626	<.0001
X	1	1.0000	0	.	.

Profile Likelihood Confidence Interval for Parameters
Parameter	Estimate	95% Confidence Limits
Intercept	-4.6605	-4.8057	-4.5219

Results of fitting this constant risk model are shown in Output 39.10.1. The maximum likelihood estimate of $\beta_0=\log(\mu)$ and its estimated standard error are $\hat{\beta}_0=-4.6605$ and $\hat{\sigma}_{\hat{\beta}_0}=0.0725$ ,respectively. The infection rate is estimated as

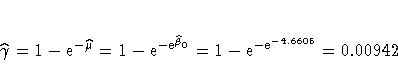
$\hat{\gamma}=1-{\rm e}^{-\hat{\mu}} =1-{\rm e}^{-{\rm e}^{\hat{\beta}_0}} =1-{\rm e}^{-{\rm e}^{-4.6605}} =0.00942$

The 95% confidence interval for $\gamma$ , obtained by back-transforming the 95% confidence interval for $\beta_0$ ,is (0.0082, 0.0011); that is, there is a 95% chance that, in repeated sampling, the interval of 8 to 11 infections per thousand individuals contains the true infection rate.

The goodness of fit statistics for the constant risk model are statistically significant (p < 0.0001), indicating that the assumption of constant risk of infection is not correct. You can fit a more extensive model by allowing a separate risk of infection for each age group. Suppose $\mu_i$ is the mean number of infections per year for the ith age group. The probability of seropositive for the ith group with age midpoint A_i is $p_i=1-\exp(-\mu_i A_i)$ , so that

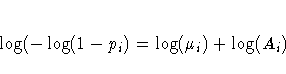
$\log(-\log(1-p_i)=\log(\mu_i) + \log(A_i)$

In the following SAS statements, nine dummy variables (agegrp1 -agegrp9) are created as the design variables for the age groups. PROC LOGISTIC is invoked to fit a complementary log-log model that contains agegrp1 -agegrp9 as the only explanatory variables with no intercept term and with X=log(A) as an offset term. Note that $\log(\mu_i)$ is the regression parameter associated with agegrpi.

   data two;
      array agegrp(9) agegrp1-agegrp9 (0 0 0 0 0 0 0 0 0);
      set sero;
      agegrp[group]=1;
      output;
      agegrp[group]=0;
   run;
   proc logistic data=two;
      model R/N=agegrp1-agegrp9 / offset=X
                                  noint
                                  link=cloglog
                                  clparm=pl;
      title 'Infectious Rates and 95% Confidence Intervals';
   run;

Output 39.10.2: Modeling Separate Risk of Infection

Infectious Rates and 95% Confidence Intervals

The LOGISTIC Procedure

Analysis of Maximum Likelihood Estimates
Parameter	DF	Estimate	Standard Error	Chi-Square	Pr > ChiSq
agegrp1	1	-3.1048	0.3536	77.0877	<.0001
agegrp2	1	-4.4542	0.4083	119.0164	<.0001
agegrp3	1	-4.2769	0.2358	328.9593	<.0001
agegrp4	1	-4.7761	0.2674	319.0600	<.0001
agegrp5	1	-4.7165	0.2238	443.9920	<.0001
agegrp6	1	-4.5012	0.1606	785.1350	<.0001
agegrp7	1	-5.4252	0.2296	558.1114	<.0001
agegrp8	1	-4.9987	0.2008	619.4666	<.0001
agegrp9	1	-4.1965	0.1559	724.3157	<.0001
X	1	1.0000	0	.	.

Profile Likelihood Confidence Interval for Parameters
Parameter	Estimate	95% Confidence Limits
agegrp1	-3.1048	-3.8880	-2.4833
agegrp2	-4.4542	-5.3769	-3.7478
agegrp3	-4.2769	-4.7775	-3.8477
agegrp4	-4.7761	-5.3501	-4.2940
agegrp5	-4.7165	-5.1896	-4.3075
agegrp6	-4.5012	-4.8333	-4.2019
agegrp7	-5.4252	-5.9116	-5.0063
agegrp8	-4.9987	-5.4195	-4.6289
agegrp9	-4.1965	-4.5164	-3.9037

Table 39.3: Infection Rate in One Year

	Number Infected per 1000 People
Age	Point	95% Confidence Limits
Group	Estimate	Lower	Upper
1	44	20	80
2	12	5	23
3	14	8	21
4	8	5	14
5	9	6	13
6	11	8	15
7	4	3	7
8	7	4	10
9	15	11	20

Results of fitting the model for separate risk of infection are shown in Output 39.10.2. For the first age group, the point estimate of $\log(\mu_1)$ is -3.1048. This translates into an infection rate of 1-exp(-exp(-3.1048)) = 0.0438. A 95% confidence interval for the infection rate is obtained by transforming the 95% confidence interval for $\log(\mu_1)$ .For the first age group, the lower and upper confidence limits are 1-exp(-exp(-3.8880) = 0.0203 and 1-exp(-exp(-2.4833)) = 0.0801, respectively. Table 39.3 shows the estimated infection rate in one year's time for each age group. Note that the infection rate for the first age group is high compared to the other age groups.

Chapter Contents
Previous
Next
Top