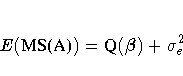Tests of Effects

Introduction to Analysis-of-Variance Procedures

Tests of Effects

Analysis of variance tests are constructed by comparing independent mean squares. To test a particular null hypothesis, you compute the ratio of two mean squares that have the same expected value under that hypothesis; if the ratio is much larger than 1, then that constitutes significant evidence against the null. In particular, in an analysis-of-variance model with fixed effects only, the expected value of each mean square has two components: quadratic functions of fixed parameters and random variation. For example, for a fixed effect called A, the expected value of its mean square is

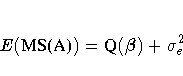
$E({MS(A)}) = Q({{\beta}}) + {\sigma}_e^2$

Under the null hypothesis of no A effect, the fixed portion Q(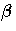 ${{\beta}}$ ) of the expected mean square is zero. This mean square is then compared to another mean square, say MS(E), that is independent of the first and has expected value $\sigma_e^2$ . The ratio of the two mean squares

F = [ MS(A)/ MS(E)]

has the F distribution under the null hypothesis. When the null hypothesis is false, the numerator term has a larger expected value, but the expected value of the denominator remains the same. Thus, large F values lead to rejection of the null hypothesis. The probability of getting an F value at least as large as the one observed given that the null hypothesis is true is called the significance probability value (or the p-value). A p-value of less than 0.05, for example, indicates that data with no real A effect will yield F values as large as the one observed less than 5% of the time. This is usually considered moderate evidence that there is a real A effect. Smaller p-values constitute even stronger evidence. Larger p-values indicate that the effect of interest is less than random noise. In this case, you can conclude either that there is no effect at all or that you do not have enough data to detect the differences being tested.

Chapter Contents
Previous
Next
Top