General Linear Models

Introduction to Analysis-of-Variance Procedures

General Linear Models

An analysis-of-variance model can be written as a linear model, which is an equation that predicts the response as a linear function of parameters and design variables. In general,

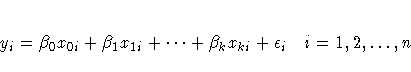
$y_i = \beta_0 x_{0i} + \beta_1 x_{1i} + ... + \beta_k x_{ki} + \epsilon_i i=1, 2, ... , n$

where y_i is the response for the ith observation, $\beta_k$ are unknown parameters to be estimated, and x_ij are design variables. Design variables for analysis of variance are indicator variables; that is, they are always either 0 or 1.

The simplest model is to fit a single mean to all observations. In this case there is only one parameter, $\beta_0$ , and one design variable, x_0i, which always has the value of 1:

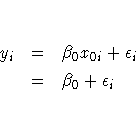
$y_i & = & \beta_0 x_{0i} + \epsilon_i \ & = & \beta_0 + \epsilon_i$

The least-squares estimator of $\beta_0$ is the mean of the y_i. This simple model underlies all more complex models, and all larger models are compared to this simple mean model. In writing the parameterization of a linear model, $\beta_0$ is usually referred to as the intercept.

A one-way model is written by introducing an indicator variable for each level of the classification variable. Suppose that a variable A has four levels, with two observations per level. The indicator variables are created as follows:

Intercept	A1	A2	A3	A4
1	1	0	0	0
1	1	0	0	0
1	0	1	0	0
1	0	1	0	0
1	0	0	1	0
1	0	0	1	0
1	0	0	0	1
1	0	0	0	1

The linear model for this example is

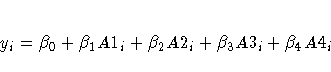
$y_i = \beta_0 + \beta_1 A1_i + \beta_2 A2_i + \beta_3 A3_i + \beta_4 A4_i$

To construct crossed and nested effects, you can simply multiply out all combinations of the main-effect columns. This is described in detail in "Specification of Effects" in Chapter 30, "The GLM Procedure."

Chapter Contents
Previous
Next
Top