Example 66.1: Mammals' Teeth
The following data give the numbers of different kinds of teeth for a
variety of mammals. The mammals are clustered by average linkage using
the CLUSTER procedure (Output 66.1.1). The PROC TREE statement
uses the average-linkage distance as the height axis, which is the default,
and creates a horizontal high-resolution graphics tree (Output 66.1.2).
data teeth;
title 'Mammals'' Teeth';
input mammal $ 1-16 @21 (v1-v8) (1.);
label V1='Right Top Incisors'
V2='Right Bottom Incisors'
V3='Right Top Canines'
V4='Right Bottom Canines'
V5='Right Top Premolars'
V6='Right Bottom Premolars'
V7='Right Top Molars'
V8='Right Bottom Molars';
datalines;
Brown Bat 23113333
Mole 32103333
Silver Hair Bat 23112333
Pigmy Bat 23112233
House Bat 23111233
Red Bat 13112233
Pika 21002233
Rabbit 21003233
Beaver 11002133
Groundhog 11002133
Gray Squirrel 11001133
House Mouse 11000033
Porcupine 11001133
Wolf 33114423
Bear 33114423
Raccoon 33114432
Marten 33114412
Weasel 33113312
Wolverine 33114412
Badger 33113312
River Otter 33114312
Sea Otter 32113312
Jaguar 33113211
Cougar 33113211
Fur Seal 32114411
Sea Lion 32114411
Grey Seal 32113322
Elephant Seal 21114411
Reindeer 04103333
Elk 04103333
Deer 04003333
Moose 04003333
;
options pagesize=60 linesize=110;
proc cluster method=average std pseudo noeigen outtree=tree;
id mammal;
var v1-v8;
run;
proc tree graphics horizontal;
run;
Output 66.1.1 displays the information on how the clusters are
joined. For example, the cluster history shows that
the observations Wolf and Bear form cluster 29, which is merged
with Raccoon to form cluster 11.
Output 66.1.1: Output from PROC CLUSTER
|
| The CLUSTER Procedure |
| Average Linkage Cluster Analysis |
| The data have been standardized to mean 0 and variance 1 |
| Root-Mean-Square Total-Sample Standard Deviation = 1 |
| Root-Mean-Square Distance Between Observations = 4 |
| Cluster History |
| NCL |
Clusters Joined |
FREQ |
PSF |
PST2 |
Norm
RMS
Dist |
T
i
e |
| 31 |
Beaver |
Groundhog |
2 |
. |
. |
0 |
T |
| 30 |
Gray Squirrel |
Porcupine |
2 |
. |
. |
0 |
T |
| 29 |
Wolf |
Bear |
2 |
. |
. |
0 |
T |
| 28 |
Marten |
Wolverine |
2 |
. |
. |
0 |
T |
| 27 |
Weasel |
Badger |
2 |
. |
. |
0 |
T |
| 26 |
Jaguar |
Cougar |
2 |
. |
. |
0 |
T |
| 25 |
Fur Seal |
Sea Lion |
2 |
. |
. |
0 |
T |
| 24 |
Reindeer |
Elk |
2 |
. |
. |
0 |
T |
| 23 |
Deer |
Moose |
2 |
. |
. |
0 |
|
| 22 |
Pigmy Bat |
Red Bat |
2 |
281 |
. |
0.2289 |
|
| 21 |
CL28 |
River Otter |
3 |
139 |
. |
0.2292 |
|
| 20 |
CL31 |
CL30 |
4 |
83.2 |
. |
0.2357 |
T |
| 19 |
Brown Bat |
Silver Hair Bat |
2 |
76.7 |
. |
0.2357 |
T |
| 18 |
Pika |
Rabbit |
2 |
73.2 |
. |
0.2357 |
|
| 17 |
CL27 |
Sea Otter |
3 |
67.4 |
. |
0.2462 |
|
| 16 |
CL22 |
House Bat |
3 |
62.9 |
1.7 |
0.2859 |
|
| 15 |
CL21 |
CL17 |
6 |
47.4 |
6.8 |
0.3328 |
|
| 14 |
CL25 |
Elephant Seal |
3 |
45.0 |
. |
0.3362 |
|
| 13 |
CL19 |
CL16 |
5 |
40.8 |
3.5 |
0.3672 |
|
| 12 |
CL15 |
Grey Seal |
7 |
38.9 |
2.8 |
0.4078 |
|
| 11 |
CL29 |
Raccoon |
3 |
38.0 |
. |
0.423 |
|
| 10 |
CL18 |
CL20 |
6 |
34.5 |
10.3 |
0.4339 |
|
| 9 |
CL12 |
CL26 |
9 |
30.0 |
7.3 |
0.5071 |
|
| 8 |
CL24 |
CL23 |
4 |
28.7 |
. |
0.5473 |
|
| 7 |
CL9 |
CL14 |
12 |
25.7 |
7.0 |
0.5668 |
|
| 6 |
CL10 |
House Mouse |
7 |
28.3 |
4.1 |
0.5792 |
|
| 5 |
CL11 |
CL7 |
15 |
26.8 |
6.9 |
0.6621 |
|
| 4 |
CL13 |
Mole |
6 |
31.9 |
7.2 |
0.7156 |
|
| 3 |
CL4 |
CL8 |
10 |
31.0 |
12.7 |
0.8799 |
|
| 2 |
CL3 |
CL6 |
17 |
27.8 |
16.1 |
1.0316 |
|
| 1 |
CL2 |
CL5 |
32 |
. |
27.8 |
1.1938 |
|
|
Output 66.1.2: PROC TREE High-Resolution Graphics
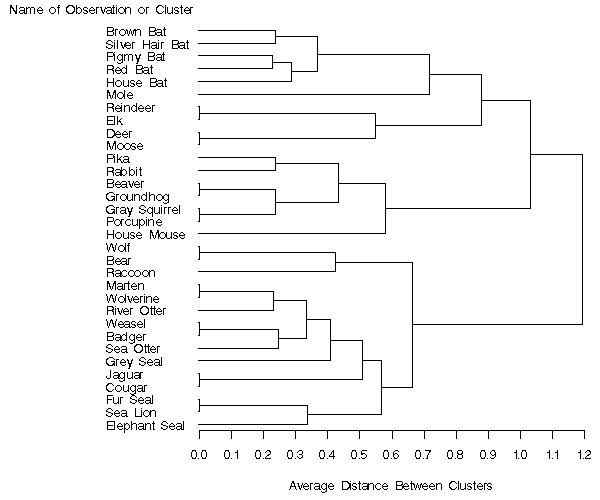
As you look from left-to-right in the diagram in Output 66.1.2, objects
and clusters are progressively joined until a single,
all-encompassing cluster is formed at the right (or root) of
the diagram. Clusters exist at each level of the diagram, and every
vertical line connects leaves and branches into
progressively larger clusters. For example, the five bats form a
cluster at the 0.6 level, while the next cluster consists only of
the mole. The observations Reindeer, Elk, Deer, and Moose
form the next cluster at the
0.6 level, the mammals Pika through House Mouse are in the fourth cluster,
The observations Wolf, Bear, and
Raccoon form the fifth cluster, while the last cluster
contains the observations Marten through Elephant Seal.
The following statements create the same tree with line printer graphics
in a vertical orientation; the tree is displayed in Output 66.1.3.
proc tree lineprinter;
run;
Output 66.1.3: PROC TREE with the LINEPRINTER Option
|
Average Linkage Cluster Analysis
Name of Observation or Cluster
S
i
l G E
v r l
e a H R e
r y o i p
B P H G P u W v S G h
r H i o R r S o s o e e r F S a
o a g R u e o q r e R l r a e u e n
w i m e s i R B u u c a M v W B y J C r a t
n r y d e n M a e n i u M c a e O e a O a o
M d D o P b a d r p o W B c r r t a d t S g u S L S
B B B B B o e E e o i b v h r i u o e o t i t s g t e u g e i e
a a a a a l e l e s k i e o e n s l a o e n e e e e a a a a o a
t t t t t e r k r e a t r g l e e f r n n e r l r r l r r l n l
A 1.5 +
v |
e |
r |
a |XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
g |XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
e 1 +XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
|XXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
D |XXXXXXXXXXX XXXXXXX XXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
i |XXXXXXXXXXX XXXXXXX XXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
s |XXXXXXXXX . XXXXXXX XXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXX
t |XXXXXXXXX . XXXXXXX XXXXXXXXXXXXX XXXXX XXXXXXXXXXXXXXXXXXXXXXX
a 0.5 +XXXXXXXXX . XXX XXX XXXXXXXXXXX . XXXXX XXXXXXXXXXXXXXXXX XXXXX
n |XXXXXXXXX . XXX XXX XXXXXXXXXXX . XXXXX XXXXXXXXXXXXX XXX XXXXX
c |XXXXXXXXX . XXX XXX XXX XXXXXXX . XXX . XXXXXXXXXXX . XXX XXXXX
e |XXX XXXXX . XXX XXX XXX XXXXXXX . XXX . XXXXX XXXXX . XXX XXX .
|. . . . . . XXX XXX . . XXX XXX . XXX . XXX . XXX . . XXX XXX .
B |. . . . . . XXX XXX . . XXX XXX . XXX . XXX . XXX . . XXX XXX .
e 0 +. . . . . . XXX XXX . . XXX XXX . XXX . XXX . XXX . . XXX XXX .
t
w
|
|
As you look up from the bottom of the diagram, objects
and clusters are progressively joined until a single,
all-encompassing cluster is formed at the top (or root) of
the diagram. Clusters exist at each level of the diagram.
For example, the unbroken line of Xs at the left-most side of
the 0.6 level indicates that the five bats have formed a cluster.
The next cluster is represented by a period
because it contains only one mammal, Mole.
Reindeer, Elk, Deer, and Moose
form the next cluster, indicated by Xs again. The mammals Pika
through House Mouse are in the fourth cluster. The observations
Wolf, Bear, and Raccoon
form the fifth cluster, while the last cluster contains the
observations Marten through
Elephant Seal.
The next statement sorts the
clusters at each branch in order of formation and uses the number of
clusters as the height axis.
The resulting tree is displayed in Output 66.1.4.
proc tree sort height=n horizontal;
run;
Output 66.1.4: PROC TREE with SORT and HEIGHT= Options
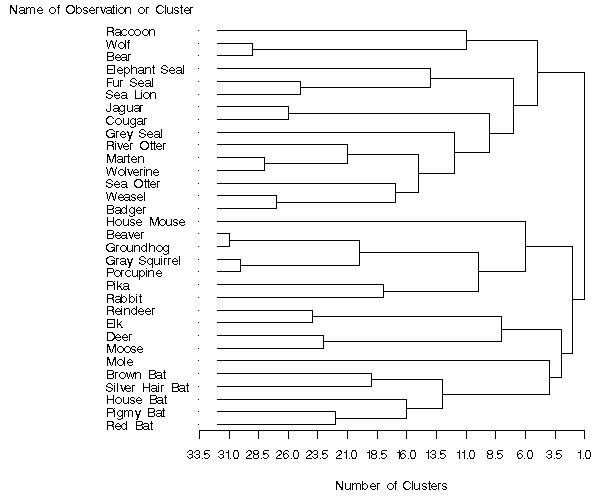
Because the CLUSTER procedure always produces binary trees, the
number of internal (root and branch) nodes in the tree is one less
than the number of leaves.
Therefore 31 clusters are formed from the 32 mammals in the input
data set.
These are represented by the 31 vertical line segments in the
tree diagram, each at a different value along the horizontal axis.
As you examine the tree from left to right, the first vertical
line segment is where Beaver and Groundhog are clustered and the
number of clusters is 31.
The next cluster is formed from Gray Squirrel and Porcupine.
The third contains Wolf and Bear.
Note how the tree graphically displays the clustering order information
that was presented in tabular form by the CLUSTER procedure in
Output 66.1.1.
The same clusters as in Output 66.1.2 and Output 66.1.3 can be seen at
the six-cluster level of the tree diagram in Output 66.1.4, although the SORT
and HEIGHT= options make them appear in a different order.
The following
statements create these six clusters and display them in Output 66.1.5.
The PROC TREE statement produces no
output but creates an output data set indicating the cluster to which
each observation belongs at the six-cluster level in the tree.
proc tree noprint out=part nclusters=6;
id mammal;
copy v1-v8;
proc sort;
by cluster;
proc print label uniform;
id mammal;
var v1-v8;
format v1-v8 1.;
by cluster;
run;
Output 66.1.5: PROC TREE OUT= Data Set
|
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Beaver |
1 |
1 |
0 |
0 |
2 |
1 |
3 |
3 |
| Groundhog |
1 |
1 |
0 |
0 |
2 |
1 |
3 |
3 |
| Gray Squirrel |
1 |
1 |
0 |
0 |
1 |
1 |
3 |
3 |
| Porcupine |
1 |
1 |
0 |
0 |
1 |
1 |
3 |
3 |
| Pika |
2 |
1 |
0 |
0 |
2 |
2 |
3 |
3 |
| Rabbit |
2 |
1 |
0 |
0 |
3 |
2 |
3 |
3 |
| House Mouse |
1 |
1 |
0 |
0 |
0 |
0 |
3 |
3 |
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Wolf |
3 |
3 |
1 |
1 |
4 |
4 |
2 |
3 |
| Bear |
3 |
3 |
1 |
1 |
4 |
4 |
2 |
3 |
| Raccoon |
3 |
3 |
1 |
1 |
4 |
4 |
3 |
2 |
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Marten |
3 |
3 |
1 |
1 |
4 |
4 |
1 |
2 |
| Wolverine |
3 |
3 |
1 |
1 |
4 |
4 |
1 |
2 |
| Weasel |
3 |
3 |
1 |
1 |
3 |
3 |
1 |
2 |
| Badger |
3 |
3 |
1 |
1 |
3 |
3 |
1 |
2 |
| Jaguar |
3 |
3 |
1 |
1 |
3 |
2 |
1 |
1 |
| Cougar |
3 |
3 |
1 |
1 |
3 |
2 |
1 |
1 |
| Fur Seal |
3 |
2 |
1 |
1 |
4 |
4 |
1 |
1 |
| Sea Lion |
3 |
2 |
1 |
1 |
4 |
4 |
1 |
1 |
| River Otter |
3 |
3 |
1 |
1 |
4 |
3 |
1 |
2 |
| Sea Otter |
3 |
2 |
1 |
1 |
3 |
3 |
1 |
2 |
| Elephant Seal |
2 |
1 |
1 |
1 |
4 |
4 |
1 |
1 |
| Grey Seal |
3 |
2 |
1 |
1 |
3 |
3 |
2 |
2 |
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Reindeer |
0 |
4 |
1 |
0 |
3 |
3 |
3 |
3 |
| Elk |
0 |
4 |
1 |
0 |
3 |
3 |
3 |
3 |
| Deer |
0 |
4 |
0 |
0 |
3 |
3 |
3 |
3 |
| Moose |
0 |
4 |
0 |
0 |
3 |
3 |
3 |
3 |
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Pigmy Bat |
2 |
3 |
1 |
1 |
2 |
2 |
3 |
3 |
| Red Bat |
1 |
3 |
1 |
1 |
2 |
2 |
3 |
3 |
| Brown Bat |
2 |
3 |
1 |
1 |
3 |
3 |
3 |
3 |
| Silver Hair Bat |
2 |
3 |
1 |
1 |
2 |
3 |
3 |
3 |
| House Bat |
2 |
3 |
1 |
1 |
1 |
2 |
3 |
3 |
| mammal |
Right
Top Incisors |
Right
Bottom
Incisors |
Right
Top Canines |
Right
Bottom
Canines |
Right
Top Premolars |
Right
Bottom
Premolars |
Right
Top Molars |
Right
Bottom
Molars |
| Mole |
3 |
2 |
1 |
0 |
3 |
3 |
3 |
3 |
|
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.