What's New in SAS Software

SAS/INSIGHT Software

Tables

Basic Confidence Intervals

The Confidence Intervals table gives confidence intervals for the mean, standard deviation, and variance for the confidence coefficient specified. You specify the confidence intervals either in the distribution output options dialog or from the Tables menu.

A 100(1- $\alpha$ )% confidence interval for the mean has upper and lower limits

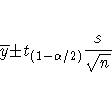
$\hspace*{0.2in} {\overline y} {+-} t_{(1 - {\alpha}/2)} \frac{s}{\sqrt{n}}$

where $t_{(1 - {\alpha}/2)}$ is the (1- $\alpha$ /2) critical value of the Student's t-statistic with n-1 degrees of freedom.

A 100(1- $\alpha$ )% confidence interval for the standard deviation has upper and lower limits

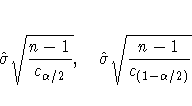
$\hspace*{0.2in} \hat{{\sigma}} \sqrt{\frac{n-1}{c_{{\alpha}/2}}}, \hat{{\sigma}} \sqrt{\frac{n-1}{c_{(1-{\alpha}/2)}}}$

where $c_{{\alpha}/2}$ and $c_{(1-{\alpha}/2)}$ are the $\alpha$ /2 and (1- $\alpha$ /2) critical values of the chi-square statistic with n-1 degrees of freedom.

A 100(1- $\alpha$ )% confidence interval for the variance has upper and lower limits equal to the squares of the corresponding upper and lower limits for the standard deviation.

Figure 1.7 shows a table of the 95% confidence intervals for mean, standard deviation, and variance.

Figure 1.7: Basic Confidence Intervals and Tests for Location Tables

Robust Measures of Scale

The sample standard deviation is a commonly used estimator of the population scale. But the estimate is sensitive to the presence of outliers and may not remain bounded when a single data point is replaced by an arbitrary number. With robust scale estimators, the estimates remain bounded even when a portion of the data points are replaced by arbitrary numbers.

A simple robust scale estimator is the interquartile range, which is the difference between the upper and lower quartiles. For a normal population, the standard deviation ${\sigma}$ can be estimated by dividing the interquartile range by 1.34898.

Gini's mean difference is also a robust estimator of the standard deviation ${\sigma}$ .It is computed as

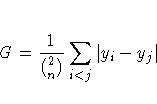
$G = \frac{1}{{2 \choose n}} \sum_{i\lt j}^{}{{| y_{i} - y_{j}|}}$

If the observations are from a normal distribution, then ${\sqrt{{\pi}}G/2}$ is an unbiased estimator of the standard deviation ${\sigma}$ .A very robust scale estimator is the MAD, the median absolute deviation about the median (Hampel, 1974.)

MAD = med_i ( | y_i - med_j(y_j) | )

where the inner median, med_j (y_j), is the median of the n observations and the outer median, med_i, is the median of the n absolute values of the deviations about the median.

For a normal distribution, 1.4826 MAD can be used to estimate the standard deviation ${\sigma}$ .

The MAD statistic has low efficient at normal distributions and it may not be appropriate for symmetric distributions. Rousseeuw and Croux (1993) proposed two new statistics as alternatives to the MAD statistic.

The first statistic is S_n,

S_n = 1.1926 med_i ( med_j (|y_i-y_j|) )

where the outer median, med_i, is the median of the n medians of { |y_i-y_j|; j = 1,2, ... , n}. To reduce the small-sample bias, c_snS_n is used to estimate the standard deviation ${\sigma}$ , where c_sn are the correction factors (Croux and Rousseeuw, 1992.)

The other statistic is Q_n,

Q_n = 2.2219 {|y_i-y_j|; i<j }_(k)

where ${k = {2 \choose h}}$ , ${h = \lfloor n/2 \rfloor +1}$ , $\lfloor {n/2} \rfloor$ is the integer part of n/2. That is, Q_n is 2.2219 times the kth order statistic of the ${{2 \choose n}}$ distances between data points.

As in S_n, c_qnQ_n is used to estimate the standard deviation ${\sigma}$ , where c_qnare the correction factors.

A Robust Measures of Scale table includes statistics of interquartile range, Gini's mean difference G, MAD, Q_n, and S_n, with their corresponding estimates of ${\sigma}$ .

Figure 1.8: Robust Measures of Scale

Tests for Normality

SAS/INSIGHT software provides tests for the null hypothesis that the input data values are a random sample from a normal distribution. These test statistics include the Shapiro-Wilk statistic, W, and statistics based on the empirical distribution function: the Kolmogorov-Smirnov, Cramer-von Mises, and Anderson-Darling statistics.

The Shapiro-Wilk statistic is the ratio of the best estimator of the variance (based on the square of a linear combination of the order statistics) to the usual corrected sum of squares estimator of the variance. W must be greater than zero and less than or equal to one, with small values of W leading to rejection of the null hypothesis of normality. Note that the distribution of W is highly skewed. Seemingly large values of W (such as 0.90) may be considered small and lead to the rejection of the null hypothesis.

The W statistic is computed when the sample size is less than or equal to 2000. When the sample size is greater than three, the coefficients for computing the linear combination of the order statistics are approximated by the method of Royston (1992).

With a sample size of three, the probability distribution of W is known and is used to determine the significance level. When the sample size is greater than three, simulation results are used to obtain the approximate normalizing transformation (Royston, 1992)

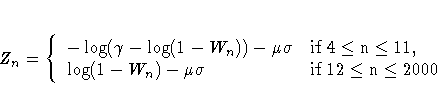
$Z_{n} = \{ -\log( \gamma - \log(1-W_n) ) - \mu \/ \sigma & \rm{if} 4 \le n \le 11, \\ \log( 1-W_n) - \mu \/ \sigma & \rm{if} 12 \le n \le 2000 .$

where ${\gamma}$ , ${\mu}$ , and ${\sigma}$ are functions of n, obtained from simulation results and Z_n is a standard normal variate with large values indicate departure from normality.

The Kolmogorov statistic assesses the discrepancy between the empirical distribution and the estimated hypothesized distribution. For a test of normality, the hypothesized distribution is a normal distribution function with parameters ${\mu}$ and ${\sigma}$ estimated by the sample mean and standard deviation. The probability of a larger test statistic is obtained by linear interpolation within the range of simulated critical values given by Stephens (1974).

The Cramer-von Mises statistic ( W²) is defined as

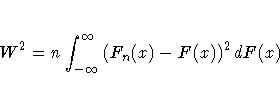
$W^2 = n \int_{-{\infty}}^{{\infty}}{(F_{n}(x) - F(x))^2\, dF(x) }$

and it is computed as

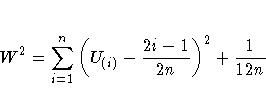
$W^2 = \sum_{i=1}^n ( U_{(i)} - \frac{2i-1}{2n} )^2 + \frac{1}{12n }$

where U_(i) = F(y_(i)), is the cumulative distribution function value at y_(i), the i-th ordered value. The probability of a larger test statistic is obtained by linear interpolation within the range of simulated critical values given by Stephens (1974).

The Anderson-Darling statistic ( A²) is defined as

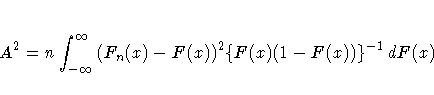
$A^2 = n \int_{-{\infty}}^{{\infty}}{(F_{n}(x) - F(x))^2 \{F(x) (1-F(x))\}^{-1} \, dF(x) }$

and it is computed as

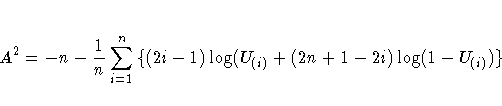
$A^2 = -n - \frac{1}n \sum_{i=1}^n{\{(2i-1) \log(U_{(i)} + (2n+1-2i) \log(1-U_{(i)}) \} }$

The probability of a larger test statistic is obtained by linear interpolation within the range of simulated critical values in D'Agostino and Stephens (1986).

A Tests for Normality table includes statistics of Shapiro-Wilk, Kolmogorov, Cramer-von Mises, and Anderson-Darling, with their corresponding p-values.

Figure 1.9: Tests for Normality and Frequency Counts Tables

Chapter Contents
Previous
Next
Top