Regular OSCILLATION, for instance, by a particle in a solid, fluid or gas, displaced from its normal position or random motion, when the force required is proportional to the displacement.
This motion may be approximated by that of the tines of a tuning fork when struck, and could be seen as a sinusoidal or SINE WAVE from the trace of a pen attached to the tine and moving against paper travelling at uniform speed. Similarly, simple harmonic motion may be derived from the projection onto the axis of a circle of a point moving with constant speed on the circumference, as shown in the diagram below.
See: CYCLE, PARTICLE VELOCITY, PERIODIC, PHASE, SOUND PRESSURE, VIBRATION. Compare: FOURIER ANALYSIS.
The angular velocity w of the motion is defined in radians per second as the angle q moved through per unit time, and is related to the FREQUENCY f by the equation:
The displacement d, whose maximum is the AMPLITUDE A, may be expressed as:
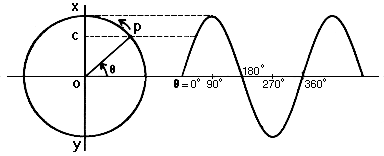
Geometric derivation of simple harmonic motion. A point p moves at constant speed on the circumference of a circle in counter-clockwise motion. Its projection OC on the vertical axis XOY is shown at right as a function of the angle q. The function described is that of a sine wave.
home