STAT 330 Lecture 28
Reading for Today's Lecture: 11.1, 11.2.
Goals of Today's Lecture:
Today's notes
Two way layouts without replicates (K=1)
We simplify the model to
The 
and 
are main effects of the two factors.
We can use the ANOVA table:
Sum of Mean
Source df Squares Square F P
Factor 1 I-1 
SS/df
Factor 2 J-1 
SS/df
Error (I-1)(J-1) 
SS/df Total n-1 
and 
.
Once one of these hypotheses is rejected we would examine confidence confidence intervals for suitable contrasts.
NOTE: There are many solutions of the equation
The data can give us guidance as to 
but cannot distinguish
between two different solutions for the given equation. This means
that the parameters 
, 
and 
are artificial. However,
for any solution of the equation we see that
This proves that 
is the same for any
solution of the equation given.
Since the are physically meaningful quantities so are the
contrasts of the form . A similar argument
applies to the s.
SAS example: ANOVA for a randomized complete blocks design
The data consist of yields of penicillin grown in 5 batches of ``corn liquour'' using one of 4 treatments. A total of 20 measurements are made and the batches of ``corn liquour'' are the blocks in which each of the 4 treatments is tried. The data came from the text by Box, Hunter and Hunter which you can consult to see a detailed discussion.
I use proc anova to test the hypotheses of no effect of treatment.
I ran the following SAS code:
options pagesize=60 linesize=80; data pencil; infile 'pencil.dat'; input blend treat yield run; proc anova data=pencil; class blend treat; model yield = blend treat; means treat blend / tukey cldiff ; run;
The line labelled model says that I am interested in the effects of the blocking variable, blend, and he factor treatment.
The output from proc anova is
The SAS System 9
08:58 Friday, November 8, 1996
Analysis of Variance Procedure
Dependent Variable: YIELD
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 7 334.00000000 47.71428571 2.53 0.0754
Error 12 226.00000000 18.83333333
Corrected Total 19 560.00000000
R-Square C.V. Root MSE YIELD Mean
0.596429 5.046208 4.3397389 86.000000
Source DF Anova SS Mean Square F Value Pr > F
BLEND 4 264.00000000 66.00000000 3.50 0.0407
TREAT 3 70.00000000 23.33333333 1.24 0.3387
Tukey's Studentized Range (HSD) Test for variable: YIELD
NOTE: This test controls the type I experimentwise error rate.
Alpha= 0.05 Confidence= 0.95 df= 12 MSE= 18.83333
Critical Value of Studentized Range= 4.199
Minimum Significant Difference= 8.1485
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
TREAT Confidence Between Confidence
Comparison Limit Means Limit
C - D -5.149 3.000 11.149
C - B -4.149 4.000 12.149
C - A -3.149 5.000 13.149
D - C -11.149 -3.000 5.149
D - B -7.149 1.000 9.149
D - A -6.149 2.000 10.149
B - C -12.149 -4.000 4.149
B - D -9.149 -1.000 7.149
B - A -7.149 1.000 9.149
A - C -13.149 -5.000 3.149
A - D -10.149 -2.000 6.149
A - B -9.149 -1.000 7.149
Tukey's Studentized Range (HSD) Test for variable: YIELD
NOTE: This test controls the type I experimentwise error rate.
Alpha= 0.05 Confidence= 0.95 df= 12 MSE= 18.83333
Critical Value of Studentized Range= 4.508
Minimum Significant Difference= 9.781
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
BLEND Confidence Between Confidence
Comparison Limit Means Limit
1 - 4 -5.781 4.000 13.781
1 - 3 -2.781 7.000 16.781
1 - 2 -0.781 9.000 18.781
1 - 5 0.219 10.000 19.781 ***
4 - 1 -13.781 -4.000 5.781
4 - 3 -6.781 3.000 12.781
4 - 2 -4.781 5.000 14.781
4 - 5 -3.781 6.000 15.781
3 - 1 -16.781 -7.000 2.781
3 - 4 -12.781 -3.000 6.781
3 - 2 -7.781 2.000 11.781
3 - 5 -6.781 3.000 12.781
2 - 1 -18.781 -9.000 0.781
2 - 4 -14.781 -5.000 4.781
2 - 3 -11.781 -2.000 7.781
2 - 5 -8.781 1.000 10.781
5 - 1 -19.781 -10.000 -0.219 ***
5 - 4 -15.781 -6.000 3.781
5 - 3 -12.781 -3.000 6.781
5 - 2 -10.781 -1.000 8.781
Notice how few of the blend differences are judged significant by Tukey.
Blend is barely significant and there is no apparent treatment effect.
Note, however, that testing the hypothesis about blend is usually of little
interest; blocking factors almost always influence the response or you
wouldn't block on them.
Confidence intervals for contrasts
Assume: 
no interactions has been accepted (or K=1 and no
interactions has been assumed).
We can get confidence intervals for by either
a t method or a Tukey method.
t intervals are of the form
based on the observation that the standard error of the difference between two averages can be computed as usual.
Remarks:
. 
by "pooling" the Interaction Sum of Squares with the Error SS.
To do this last we take the two lines {
| Sum of | |||
| Source | df | Squares | |
| Interaction | (I-1)(J-1) |
|  |
| Error | IJ(K-1) | 
| |
| and add them together to get | |||
| Error | (I-1)(J-1)+IJ(K-1) | Int'n SS + Old ESS | |
and more powerful tests for main effects
IF
for all i,j is true.
Disadvantage: the test of this null hypothesis of no interactions has low
power and if for all i,j is false then the
new ESS is inflated.
Simultaneous confidence intervals
Notice that from the model equation (the overlines indicate averaging over j and k)
so that
is simply a difference between two averages of JK 
random
variables. This means we can apply the Tukey idea with J replaced by
JK to get the interval
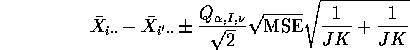
where 
is the degrees of freedom associated with the MSE.
Examples:
In the plaster hardness example we have the output from the means statement in proc anova:
Tukey's Studentized Range (HSD) Test for variable: HARDNESS
NOTE: This test controls the type I experimentwise error rate.
Alpha= 0.05 Confidence= 0.95 df= 9 MSE= 8.166667
Critical Value of Studentized Range= 3.948
Minimum Significant Difference= 4.6066
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
SAND Confidence Between Confidence
Comparison Limit Means Limit
30 - 15 -2.773 1.833 6.440
30 - 0 1.227 5.833 10.440 ***
15 - 30 -6.440 -1.833 2.773
15 - 0 -0.607 4.000 8.607
0 - 30 -10.440 -5.833 -1.227 ***
0 - 15 -8.607 -4.000 0.607
Tukey's Studentized Range (HSD) Test for variable: HARDNESS
NOTE: This test controls the type I experimentwise error rate.
Alpha= 0.05 Confidence= 0.95 df= 9 MSE= 8.166667
Critical Value of Studentized Range= 3.948
Minimum Significant Difference= 4.6066
Comparisons significant at the 0.05 level are indicated by '***'.
Simultaneous Simultaneous
Lower Difference Upper
FIBRE Confidence Between Confidence
Comparison Limit Means Limit
50 - 25 -4.607 0.000 4.607
50 - 0 0.060 4.667 9.273 ***
25 - 50 -4.607 0.000 4.607
25 - 0 0.060 4.667 9.273 ***
0 - 50 -9.273 -4.667 -0.060 ***
0 - 25 -9.273 -4.667 -0.060 ***
showing clear differences between the 30% and 0% sand levels and
between the 0% level of fibre and the other two levels.
Remark: We have two sets of Tukey intervals in this output and the probability of no errors in either one of them is less than 0.95. The best we can say is
which is called Bonferroni's inequality.
Further topics in 2 way ANOVA
Justification for F tests: In practice experimental units are not
a random sample from a population of experimental units but rather just a
convenient set of such units. However, random assignment of experimental units
to levels of a factor justifies (mathematically and approximately) use of the
standard F tests for main effects of that factor. NOTE: this does not apply
to effects of blocking factors. To test the null hypothesis of no block effects
we must believe the sampling model: that the 
s are iid mean 0 variance
.
Random effects: In the penicillin example the batches of corn liquor are just 5 of many possible batches. We often model the batches (blocks) as a random sample from a population of possible blocks. We write the model equation
and assume that the are independent 
random variables. This has no impact on the analysis if there are no
replicates, but the formula for the expected mean square due to blocks
is changed. If, however, there are replicates then:
where now the and 
values are random: is
and 
is 
. The resulting
expected mean squares are:
| Source | Expected MS | |
| Treatment | 
| |
| Blocks | | 
|
| Interactions | | 
|
| Error |
| |
| Total |
The usual test of is based on
with P-values coming from the F distribution. The point is that the expected
values of the two mean squares in this statistic differ only in the term depending
on s.